Intermediate Geometry - Learning for Knowledge
... thickness. Points are the basic building blocks of lines and curves. Lines: Lines are made up of a number of points positioned side by side. A line is a geometrical figure which has length but no breadth. A line drawn between 2 points is known as a line segment. A line is considered as a straight li ...
... thickness. Points are the basic building blocks of lines and curves. Lines: Lines are made up of a number of points positioned side by side. A line is a geometrical figure which has length but no breadth. A line drawn between 2 points is known as a line segment. A line is considered as a straight li ...
Chapter 3 - TeacherWeb
... both supplementary by the Consecutive Interior Angles Theorem. ∠ MNQ > ∠QPM by the Congruent Supplements Theorem. ∠ NMP and ∠ QPM, and ∠ QPM and ∠ PQN are both supplementary by the Consecutive Interior Angles Theorem. ∠ NMP > ∠ PQN by the ...
... both supplementary by the Consecutive Interior Angles Theorem. ∠ MNQ > ∠QPM by the Congruent Supplements Theorem. ∠ NMP and ∠ QPM, and ∠ QPM and ∠ PQN are both supplementary by the Consecutive Interior Angles Theorem. ∠ NMP > ∠ PQN by the ...
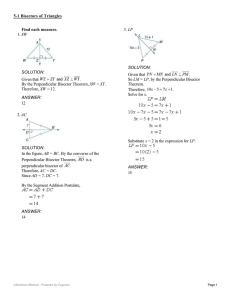
Find each measure. 1. XW SOLUTION: Given that By
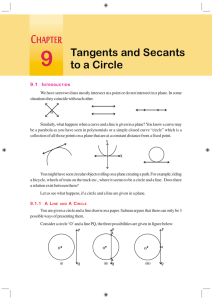
... bisector? You can prove it in two parts - first, that and are perpendicular to each other and then, that is bisected. This will involve proving two triangles are congruent so that you can get congruent corresponding parts (CPCTC). Start by considering which triangles you can make congruent to each ...
... bisector? You can prove it in two parts - first, that and are perpendicular to each other and then, that is bisected. This will involve proving two triangles are congruent so that you can get congruent corresponding parts (CPCTC). Start by considering which triangles you can make congruent to each ...
What is Hyperbolic Geometry? - School of Mathematics, TIFR
... Department of Mathematics, RKM Vivekananda University. ...
... Department of Mathematics, RKM Vivekananda University. ...
Postulates Theorems and Corollaries
... points there is exactly one plane containing them. Post. 1-1-3: If two points lie in a plane, then the line containing those points lies in the plane. Post. 1-1-4: If two lines intersect, then they intersect in exactly one point. ...
... points there is exactly one plane containing them. Post. 1-1-3: If two points lie in a plane, then the line containing those points lies in the plane. Post. 1-1-4: If two lines intersect, then they intersect in exactly one point. ...