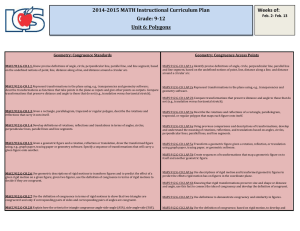
What We Knew About Hyperbolic Geometry Before We Knew
... Euclid defines parallel with definition, “Parallel straight lines are straight lines which, being in the same plane and being produced indefinitely in both directions, do not meet one another in either direction.” We may also consider an alternative definition of parallel given by Posidonius (1st Ce ...
... Euclid defines parallel with definition, “Parallel straight lines are straight lines which, being in the same plane and being produced indefinitely in both directions, do not meet one another in either direction.” We may also consider an alternative definition of parallel given by Posidonius (1st Ce ...
Discovery Learning Notes
... be infinite). Specific subsets of U will be called lines and we will denote lines by `, `1 , and `2 (though again there might be an infinite number of lines). It is usually our axioms that tell us which subsets can be lines. The only properties about the universe and its points and line are those in ...
... be infinite). Specific subsets of U will be called lines and we will denote lines by `, `1 , and `2 (though again there might be an infinite number of lines). It is usually our axioms that tell us which subsets can be lines. The only properties about the universe and its points and line are those in ...
Geometry - University of Hawaii Mathematics
... falling upon it from one point among those lying within the figure are equal to one another. 21. Rectilineal figures are those which are contained by straight lines, trilateral figures being those contained by three, ... 23. Parallel straight lines are straight lines which being in the same plane an ...
... falling upon it from one point among those lying within the figure are equal to one another. 21. Rectilineal figures are those which are contained by straight lines, trilateral figures being those contained by three, ... 23. Parallel straight lines are straight lines which being in the same plane an ...
Chapter 8
... Parallelogram: opposite sides are parallel and congruent. Opposite angles are congruent. Rectangle: Parallelogram with four right angles Rhombus: Parallelogram with four congruent sides, opposite angles are congruent Square: Parallelogram with four congruent sides and four right angles. Trapezoid: O ...
... Parallelogram: opposite sides are parallel and congruent. Opposite angles are congruent. Rectangle: Parallelogram with four right angles Rhombus: Parallelogram with four congruent sides, opposite angles are congruent Square: Parallelogram with four congruent sides and four right angles. Trapezoid: O ...