Download Document

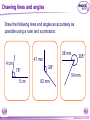
KS3 Mathematics
S6 Construction and loci
1 of 41
© Boardworks Ltd 2004
Contents
S6 Construction and loci
S6.1 Drawing lines and angles
S6.2 Constructing triangles
S6.3 Constructing lines and angles
S6.4 Constructing nets
N6.5 Loci
2 of 41
© Boardworks Ltd 2004
Equipment needed for constructions
Before you begin make sure you have the following
equipment:
3 of 41
A ruler marked in
cm and mm
A protractor
A compass
A sharp pencil
© Boardworks Ltd 2004
Drawing lines
To draw a line of given length use a ruler and a sharp pencil.
For example, draw line segment AB of length 56 mm.
Draw a point and label it A.
Place your ruler with 0 mm at the point A.
Mark point B at 56 mm.
Draw line segment AB.
B
A
0
4 of 41
1
2
3
4
5
6
7
© Boardworks Ltd 2004
Drawing angles
To draw a given angle use a ruler, a protractor and a sharp
pencil.
For example, construct
ABC = 68°
Start by drawing line segment AB.
C
Place a protractor so that point B
is at the centre of the small circle.
Reading the scale so that 0° is on
the line, mark point C at 68°.
A
5 of 41
B
Use a ruler to draw a line from
point B to point C.
© Boardworks Ltd 2004
Drawing reflex angles
To draw a reflex angle we
can use a 360° protractor.
To draw a reflex angle using a 180° protractor, start by
subtracting the angle from 360°.
For example, to draw an angle of 243° work out 360° – 243°.
360° – 243° = 117°.
Draw an angle of 117°.
The reflex angle will be
the required 243°.
6 of 41
117°
243°
© Boardworks Ltd 2004
Drawing lines and angles
Draw the following lines and angles as accurately as
possible using a ruler and a protractor.
38 mm
47 mm
4 cm
78°
305°
128°
54 mm
5 cm
7 of 41
62 mm
© Boardworks Ltd 2004
Contents
S6 Construction and loci
S6.1 Drawing lines and angles
S6.2 Constructing triangles
S6.3 Constructing lines and angles
S6.4 Constructing nets
N6.5 Loci
8 of 41
© Boardworks Ltd 2004
Constructing a triangle given SAS
How could we construct a triangle given the lengths
of two of its sides and the angle between them?
side
angle
side
The angle between the two sides is often called the
included angle.
We use the abbreviation SAS to stand for Side, Angle and
Side.
9 of 41
© Boardworks Ltd 2004
Constructing a triangle given SAS
For example, construct
and BC = 5 cm.
ABC with AB = 6 cm,
Start by drawing side AB
with a ruler.
B = 68°
C
5 cm
Use a protractor to mark an
angle of 68° from point B.
68°
A
6 cm
B
Use a ruler to draw a line of
5 cm from B to C.
Join A to C using a ruler to complete the triangle.
10 of 41
© Boardworks Ltd 2004
Constructing a triangle given ASA
How could we construct a triangle given two angles
and the length of the side between them?
angle
angle
side
The side between the two angles is often called the
included side.
We use the abbreviation ASA to stand for Angle, Side and
Angle.
11 of 41
© Boardworks Ltd 2004
Constructing a triangle given ASA
For example, construct
and
B = 115°.
ABC with AB = 10 cm,
A = 35°
C
Start by drawing side AB
with a ruler.
Use a protractor to mark an
angle of 35° from point A.
Use a ruler to draw a long
line from A.
Use a protractor to mark an
angle of 115° from point B.
35°
A
10 cm
115°
B
Use a ruler to draw a line from B to meet the other line at
point C.
12 of 41
© Boardworks Ltd 2004
Constructing a triangle given SSS
How could we construct a triangle
given the lengths of three sides?
side
side
side
Hint: We would need to use a compass.
We use the abbreviation SSS to stand for Side, Side, Side.
13 of 41
© Boardworks Ltd 2004
Constructing a triangle given SSS
For example, construct ABC with AB = 4 cm, BC = 3 cm
and AC = 5 cm.
C
Start by drawing side AB with a ruler.
Use a compass and stretch
5 cm
it out to a length of 5 cm.
3 cm
Put the point of the compass at
point A and draw an arc above
A
4 cm
B
line AB.
Next, stretch the compass out to a length of 3 cm.
Put the point of the compass at point B and draw an arc
crossing over the other one. This is point C.
Draw lines AC and BC to complete the triangle.
14 of 41
© Boardworks Ltd 2004
Constructing a triangle given RHS
Remember, the longest side in a right-angled triangle is
called the hypotenuse.
How could we construct a right-angled triangle given the
right angle, the length of the hypotenuse and the length of
one other side?
hypotenuse
right angle
side
We use the abbreviation RHS to stand for Right angle,
Hypotenuse and Side.
15 of 41
© Boardworks Ltd 2004
Constructing a triangle given RHS
For example, construct
and AC = 7 cm.
ABC with AB = 5 cm,
C
Start by drawing side AB
with a ruler.
Extend AB and use a
compass to construct a
perpendicular at point B.
B = 90°
7 cm
A
5 cm
B
Open the compass to 7 cm.
Place the point of the compass on A and draw an arc on the
perpendicular.
Label this point C and complete the triangle.
16 of 41
© Boardworks Ltd 2004
Constructing triangles
17 of 41
© Boardworks Ltd 2004
Contents
S6 Construction and loci
S6.1 Drawing lines and angles
S6.2 Constructing triangles
S6.3 Constructing lines and angles
S6.4 Constructing nets
N6.5 Loci
18 of 41
© Boardworks Ltd 2004
Bisecting lines
Two lines bisect each other if each line divides the other
into two equal parts.
For example, line CD bisects line AB at right angles.
C
A
B
D
We indicate equal lengths using dashes on the lines.
When two lines bisect each other at right angles we can
join the end points together to form a rhombus.
19 of 41
© Boardworks Ltd 2004
Bisecting angles
A line bisects an angle if it divides it into two equal
angles.
For example, in this diagram line BD bisects
ABC.
A
D
B
20 of 41
C
© Boardworks Ltd 2004
The perpendicular bisector of a line
We can construct the perpendicular bisector of a line
segment AB using a ruler and a compass as follows.
Place the point of a compass
at point A and open it so that
it is more than half the size of
the line.
Draw an arc.
A
B
Move the point of the
compass to point B and draw
an other arc.
Join the points where the arcs cross to form the
perpendicular bisector.
21 of 41
© Boardworks Ltd 2004
The bisector of an angle
We can construct the bisector of an angle ABC using a
ruler and a compass as follows.
A
Place the point of a compass
at point B and draw an arc
P
that cuts lines AB and BC.
R
Place the point of the
compass at point P and draw
an arc.
Repeat this with the point of
the compass at point Q.
B
Q
C
Join point B to the point where the two arcs cross to make
the angle bisector.
22 of 41
© Boardworks Ltd 2004
The perpendicular from a point to a line
We can construct the perpendicular from point P to line
segment AB using a ruler and a compass as follows.
Start by placing the point of the
compass at point P and use it to
draw an arc crossing the line
segment AB at points Q and R.
Place the point of the compass
at point Q and draw an arc
below the line.
P
Q
R
A
B
Repeat this at point R.
Join point P to the points where the arcs cross to form the
perpendicular from point P to line segment AB.
23 of 41
© Boardworks Ltd 2004
The perpendicular from a point on a line
We can construct the perpendicular from the point P on line
segment AB using a ruler and a compass as follows.
Start by placing the point of the
compass at point P and use it to
draw an arc crossing the line
segment AB at points Q and R.
Open the compass out a bit
more and place the point at Q
to draw an arc.
Q
P
R
A
B
Repeat this at point R without changing the compass.
Join point the points where the arcs cross to form the
perpendicular through point P and line segment AB.
24 of 41
© Boardworks Ltd 2004
Contents
S6 Construction and loci
S6.1 Drawing lines and angles
S6.2 Constructing triangles
S6.3 Constructing lines and angles
S6.4 Constructing nets
N6.5 Loci
25 of 41
© Boardworks Ltd 2004
Constructing nets
Before constructing an accurate net of a solid shape it is
sensible to start by making a sketch of how we expect the
completed net to look.
Remember, in maths, a sketch is a diagram that is not
drawn to scale. We should still use a ruler to do this.
Suppose we want to construct the net of a cuboid of length
4 cm, width 2 cm and height 1 cm.
We can sketch the net on squared paper as follows:
These
are tabs.
26 of 41
© Boardworks Ltd 2004
Construct a cuboid
Construct nets for the following cuboids on plain paper.
5 cm
3 cm
4 cm
2 cm
27 of 41
3 cm
1.5 cm
© Boardworks Ltd 2004
Construct the net of a tetrahedron
Construct the net of a square-based pyramid with
base 3 cm by 3 cm and sloping edges of length 4 cm.
Your sketch should look
something like this.
3 cm
3 cm
4 cm
3 cm
3 cm
28 of 41
© Boardworks Ltd 2004
Contents
S6 Construction and loci
S6.1 Drawing lines and angles
S6.2 Constructing triangles
S6.3 Constructing lines and angles
S6.4 Constructing nets
N6.5 Loci
29 of 41
© Boardworks Ltd 2004
Imagining paths
A locus is a set of points that satisfy a rule or set of rules.
The plural of locus is loci.
We can think of a locus as a path traced out by a moving
point.
For example,
Imagine the path of a golf ball
as it is driven on to the green.
The ball bounces several
times and drops into the hole.
30 of 41
© Boardworks Ltd 2004
Imagining paths
The path of the ball might look something like this:
The red dotted line shows the locus of the points traced out
by the golf ball.
31 of 41
© Boardworks Ltd 2004
Imagining paths
A helicopter takes off and rises
to a height of 30 m.
It accelerates forward and rises
to 1000 m where it levels out
then continues on its way.
Can you imagine the path traced out by the helicopter?
How could you represent the path in two dimensions?
What about in three dimensions?
32 of 41
© Boardworks Ltd 2004
Imagining paths
A nervous woman paces up and
down in one of the capsules on
the Millennium Eye as she
‘enjoys’ the view.
Can you imagine the path traced out by the woman?
How could you represent the path in two dimensions?
What about in three dimensions?
33 of 41
© Boardworks Ltd 2004
Imagining paths
A man has been out for the
evening, has locked himself out
of his flat and has to climb the
spiral fire escape.
Can you imagine the path traced out by the man?
How could you represent the path in two dimensions?
What about in three dimensions?
34 of 41
© Boardworks Ltd 2004
Imagining paths
A spider is hanging motionless
from a web.
Imagine moving your hand so
that the tip of your finger is
always 10 cm from the spider.
Can you imagine the path traced out by your finger tip?
How could you represent the path in two dimensions?
What about in three dimensions?
35 of 41
© Boardworks Ltd 2004
Walking turtle
36 of 41
© Boardworks Ltd 2004
The locus of points from a fixed point
Imagine placing counters so that their centres are always 5
cm from a fixed point P.
5 cm
P
Describe the locus made by the counters.
The locus is a circle with a radius of 5 cm and centre at point P.
37 of 41
© Boardworks Ltd 2004
The locus of points from a line segment
Imagine placing counters that their centres are always 3 cm
from a line segment AB.
A
B
Describe the locus made by the counters.
The locus is a pair of parallel lines 3 cm either side of AB. The
ends of the line AB are fixed points, so we draw semi-circles
of radius 3 cm.
38 of 41
© Boardworks Ltd 2004
The locus of points from two fixed points
Imagine placing counters so that they are always an equal
distance from two fixed points P and Q.
P
Q
Describe the locus made by the counters.
The locus is the perpendicular bisector of the line joining the
two points.
39 of 41
© Boardworks Ltd 2004
The locus of points from two lines
Imagine placing counters so that they are an equal distance
from two straight lines that meet at an angle.
Describe the locus made by the counters.
The locus is the angle bisector of the angle where the two lines
intersect.
40 of 41
© Boardworks Ltd 2004
Rolling shapes along lines
41 of 41
© Boardworks Ltd 2004