10mod_phys
... • DeBroglie required that the electron in the Bohr atom have a wavelength so that an integral number of them would fit on a Bohr Orbit: 2πrn = n λ ; n=1, 2, 3, …. • Then with λ = h/(mv) • We get: 2πrn = n h/mv • Or: mvrn = n [h/(2π)] • Which is Bohr’s Quantization Condition. ...
... • DeBroglie required that the electron in the Bohr atom have a wavelength so that an integral number of them would fit on a Bohr Orbit: 2πrn = n λ ; n=1, 2, 3, …. • Then with λ = h/(mv) • We get: 2πrn = n h/mv • Or: mvrn = n [h/(2π)] • Which is Bohr’s Quantization Condition. ...
Key Concepts for Exam #2
... If the frequency of incident light is above the threshold frequency, then as the intensity of light increases, the kinetic energy of ejected electrons remains constant and the number of electrons increases. In addition, as the frequency of light increases, the kinetic energy of ejected electrons inc ...
... If the frequency of incident light is above the threshold frequency, then as the intensity of light increases, the kinetic energy of ejected electrons remains constant and the number of electrons increases. In addition, as the frequency of light increases, the kinetic energy of ejected electrons inc ...
Probing the Orbital Energy of an Electron in an Atom
... or orbitals) rather than by instantaneous positions and velocities: an electron may be considered always to be (with appropriate probability) at all points of its distribution (which does not vary with time). ...
... or orbitals) rather than by instantaneous positions and velocities: an electron may be considered always to be (with appropriate probability) at all points of its distribution (which does not vary with time). ...
Document
... If one photon of electromagnetic energy (E = hf) strikes a metal surface, it causes one electron to be emitted from the metal surface if the photon's energy (hf) is equal to or greater than the work function of the metal, part of the photon's energy being used to enable the electron to escape. The r ...
... If one photon of electromagnetic energy (E = hf) strikes a metal surface, it causes one electron to be emitted from the metal surface if the photon's energy (hf) is equal to or greater than the work function of the metal, part of the photon's energy being used to enable the electron to escape. The r ...
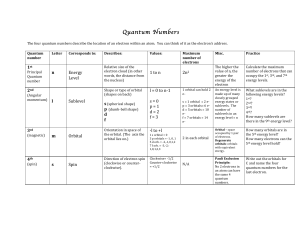
Quantum Numbers Handout File
... An!energy!level!is! made!up!of!many! closely!grouped! energy!states!or! sublevels.!!The! number!of! sublevels!in!an! energy!level!=!n! ...
... An!energy!level!is! made!up!of!many! closely!grouped! energy!states!or! sublevels.!!The! number!of! sublevels!in!an! energy!level!=!n! ...
APS104H1_20161_661461623642Lecture 2
... atom. Therefore, Heisenberg said that we shouldn't view electrons as moving in well-defined orbits about the nucleus! With Heisenberg's uncertainty principle in mind, an Austrian physicist named Erwin Schrodinger derived a set of equations or wave functions (Ψ) in 1926 for electrons. According to Sc ...
... atom. Therefore, Heisenberg said that we shouldn't view electrons as moving in well-defined orbits about the nucleus! With Heisenberg's uncertainty principle in mind, an Austrian physicist named Erwin Schrodinger derived a set of equations or wave functions (Ψ) in 1926 for electrons. According to Sc ...
Atomic units
... Electric field = e/a02 = 5.14x109 V/cm Other units: One atomic unit of magnetic field is defined for a Bohr magneton in a B field which has the energy of 13.6 eV. Or B B 13.6eV where B e / 2mc 5.788x10 5 eV / Tesla Thus 1 a.u. of magnetic field = 2.35x105 Tesla ...
... Electric field = e/a02 = 5.14x109 V/cm Other units: One atomic unit of magnetic field is defined for a Bohr magneton in a B field which has the energy of 13.6 eV. Or B B 13.6eV where B e / 2mc 5.788x10 5 eV / Tesla Thus 1 a.u. of magnetic field = 2.35x105 Tesla ...
Chapter 8 - Clayton State University
... Mechanics is a branch of physics that deals with forces and movement. Classical mechanics is based on Newton’s laws of motion. Classical mechanics deals with objects that have only particle-like properties, whose momenta and positions are completely known. Quantum mechanics deals with objects that h ...
... Mechanics is a branch of physics that deals with forces and movement. Classical mechanics is based on Newton’s laws of motion. Classical mechanics deals with objects that have only particle-like properties, whose momenta and positions are completely known. Quantum mechanics deals with objects that h ...
n-1 - KAIST
... The kinetic and potential energies are transformed into the Hamiltonian which acts upon the wavefunction to give the quantized energies of the system and the form of the wavefunction so that other properties may be calculated. The wave nature of the electron has been clearly shown in experiments lik ...
... The kinetic and potential energies are transformed into the Hamiltonian which acts upon the wavefunction to give the quantized energies of the system and the form of the wavefunction so that other properties may be calculated. The wave nature of the electron has been clearly shown in experiments lik ...
Quantum electrodynamics

In particle physics, quantum electrodynamics (QED) is the relativistic quantum field theory of electrodynamics. In essence, it describes how light and matter interact and is the first theory where full agreement between quantum mechanics and special relativity is achieved. QED mathematically describes all phenomena involving electrically charged particles interacting by means of exchange of photons and represents the quantum counterpart of classical electromagnetism giving a complete account of matter and light interaction.In technical terms, QED can be described as a perturbation theory of the electromagnetic quantum vacuum. Richard Feynman called it ""the jewel of physics"" for its extremely accurate predictions of quantities like the anomalous magnetic moment of the electron and the Lamb shift of the energy levels of hydrogen.