Math 25 — Solutions to Homework Assignment #4
... 3. A set E of real numbers is called ultra-dense if for every real numbers a < b, the interval (a, b) contains infinitely many elements of E. Prove that E is ultra-dense if and only if it is dense. Proof. Clearly, if E is ultra-dense, then it is also dense. So suppose E is dense in R. Assume there ...
... 3. A set E of real numbers is called ultra-dense if for every real numbers a < b, the interval (a, b) contains infinitely many elements of E. Prove that E is ultra-dense if and only if it is dense. Proof. Clearly, if E is ultra-dense, then it is also dense. So suppose E is dense in R. Assume there ...
Full text
... so that in this case ak+l might be in the interval (0, k + 3] ... . The proof of the theorem leads to the construction of a sequence s(N, a) with a-a and N = 0 as defined in the introduction. Now, suppose a G[0, 2] is a rational number of the form k 12m with k, m eN0. Then at is a rational number wi ...
... so that in this case ak+l might be in the interval (0, k + 3] ... . The proof of the theorem leads to the construction of a sequence s(N, a) with a-a and N = 0 as defined in the introduction. Now, suppose a G[0, 2] is a rational number of the form k 12m with k, m eN0. Then at is a rational number wi ...
Lecture 16 MATH1904 Generating Functions When faced with a
... Generating functions are power series which usually involve infinitely many terms. We would like to find simpler expressions for these series, using only a finite number of mathematical operations. These simpler expressions are called closed forms. If the terms of the sequence an are 0 from some poi ...
... Generating functions are power series which usually involve infinitely many terms. We would like to find simpler expressions for these series, using only a finite number of mathematical operations. These simpler expressions are called closed forms. If the terms of the sequence an are 0 from some poi ...
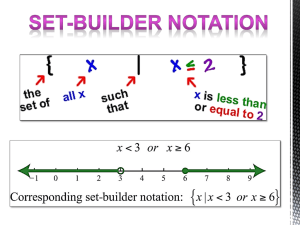
Section 1.1 The Real Number System Classify each of the numbers
... Use the number line to find the distance between the two real numbers __________________ Use an inequality symbol to represent the relationship of the two real numbers _________________ Use the formula in the box above to verify this distance ________________________________ ...
... Use the number line to find the distance between the two real numbers __________________ Use an inequality symbol to represent the relationship of the two real numbers _________________ Use the formula in the box above to verify this distance ________________________________ ...
Compactness and compactification
... to a finite number. Thus by using this compactification of the real line, we can generalise the notion of a limit, by no longer requiring that the limit has to be a real number. While there are some drawbacks to dealing with extended reals instead of the ordinary reals (for instance, one can always ...
... to a finite number. Thus by using this compactification of the real line, we can generalise the notion of a limit, by no longer requiring that the limit has to be a real number. While there are some drawbacks to dealing with extended reals instead of the ordinary reals (for instance, one can always ...
2011 U OF I FRESHMAN MATH CONTEST Solutions
... [b, c, d] = 3r 7s , where [. . . ] denotes the least common multiple). Find, with proof, a simple formula for f (r, s). Solution. The desired formula is f (r, s) = (1 + 4r + 6r2 )(1 + 4s + 6s2 ) . To prove this, note first that the four integers can have only the primes 3 and 7 in their prime factor ...
... [b, c, d] = 3r 7s , where [. . . ] denotes the least common multiple). Find, with proof, a simple formula for f (r, s). Solution. The desired formula is f (r, s) = (1 + 4r + 6r2 )(1 + 4s + 6s2 ) . To prove this, note first that the four integers can have only the primes 3 and 7 in their prime factor ...