The Musical - Year 9 – Stage 5 Good Samaritan
... To figure out the pattern we will need to look at the tonic of each scale. What is a tonic you say? I guess we need to look at scale degrees before we can solve this pattern. ...
... To figure out the pattern we will need to look at the tonic of each scale. What is a tonic you say? I guess we need to look at scale degrees before we can solve this pattern. ...
The Mathematics of Music
... Major 3rd, Minor 3rd, and Minor 6th. 12 is the smallest division of the octave that best approximates all 7 basic consonant intervals ...
... Major 3rd, Minor 3rd, and Minor 6th. 12 is the smallest division of the octave that best approximates all 7 basic consonant intervals ...
lecture16
... • Pythagorean scale • Mean-tone temperament • Scale of just intonation • Equal temperament Tuning – an adjustment of pitch in any instrument so that it corresponds to an accepted norm (scale) Temperament – a system of tuning in which the intervals deviate from acoustically pure (Pythagorean) interva ...
... • Pythagorean scale • Mean-tone temperament • Scale of just intonation • Equal temperament Tuning – an adjustment of pitch in any instrument so that it corresponds to an accepted norm (scale) Temperament – a system of tuning in which the intervals deviate from acoustically pure (Pythagorean) interva ...
lecture16
... •Pythagorean scale •Mean-tone temperament •Scale of just intonation •Equal temperament Tuning – an adjustment of pitch in any instrument so that it corresponds to an accepted norm (scale) Temperament – a system of tuning in which the intervals deviate from acoustically pure (Pythagorean) intervals I ...
... •Pythagorean scale •Mean-tone temperament •Scale of just intonation •Equal temperament Tuning – an adjustment of pitch in any instrument so that it corresponds to an accepted norm (scale) Temperament – a system of tuning in which the intervals deviate from acoustically pure (Pythagorean) intervals I ...
Musician’s Toolbox Christina Lipson ‘14 Advisor: Professor John Ridgway
... The example below charts out a Gb dim triad. The letter names must be G-B-D, so although the two m3 intervals land on notes known as A and C for the third and fifth, we must call these Bbb and Dbb. ...
... The example below charts out a Gb dim triad. The letter names must be G-B-D, so although the two m3 intervals land on notes known as A and C for the third and fifth, we must call these Bbb and Dbb. ...
Document
... Each musical note has a perceived pitch with a particular frequency (the frequency of the fundamental) Going up or down in frequency, the perceived pitch follows a pattern One cycle of pitch repetition is called an octave. ...
... Each musical note has a perceived pitch with a particular frequency (the frequency of the fundamental) Going up or down in frequency, the perceived pitch follows a pattern One cycle of pitch repetition is called an octave. ...
Tones and Semitones
... In the "C major" scale, both the first and the last notes are Cs- but how do we know what the inbetween notes are? On the piano, a C major scale uses all the white notes (so it doesn't have any sharps or flats), but on other instruments, we don't have white notes, so how do we know which notes to us ...
... In the "C major" scale, both the first and the last notes are Cs- but how do we know what the inbetween notes are? On the piano, a C major scale uses all the white notes (so it doesn't have any sharps or flats), but on other instruments, we don't have white notes, so how do we know which notes to us ...
Playing Melodically and Harmonically in Tune Michael Kimber One
... pure perfect fifth vibrates at 3/2, or 1.5, times the frequency of the lower note . Every time we tune upward a pure fifth, we multiply the frequency by 1.5. After tuning upward through four fifths (C-G, G-D, D-A, and A-E) we arrive at an E with a frequency 1.54, or 5.0625, times that of C. This dis ...
... pure perfect fifth vibrates at 3/2, or 1.5, times the frequency of the lower note . Every time we tune upward a pure fifth, we multiply the frequency by 1.5. After tuning upward through four fifths (C-G, G-D, D-A, and A-E) we arrive at an E with a frequency 1.54, or 5.0625, times that of C. This dis ...
sign lesson term definition
... natural minor scale with the 6th and 7th raised on the way up and lowered on the way down ...
... natural minor scale with the 6th and 7th raised on the way up and lowered on the way down ...
Tunings and Temperaments Powerpoint
... By extending this idea (and utilizing both black and white keys on a piano), it is possible to start at any note, go up twelve perfect Fifths, and end up at the same note from whence you started (just in a different octave) We call this the Circle of Fifths; it is an important fundamental concept th ...
... By extending this idea (and utilizing both black and white keys on a piano), it is possible to start at any note, go up twelve perfect Fifths, and end up at the same note from whence you started (just in a different octave) We call this the Circle of Fifths; it is an important fundamental concept th ...
Intervals Perfect Intervals
... Intervals An Interval is the distance between two notes. In level one we learned to name intervals by number: ...
... Intervals An Interval is the distance between two notes. In level one we learned to name intervals by number: ...
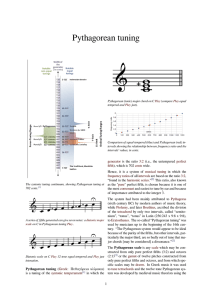
Pythagorean tuning
... As a consequence all intervals of any given type have the same size (e.g., all major thirds have the same size, all fifths have the same size, etc.). The price paid, in this case, is that none of them is justly tuned and perfectly consonant, except, of course, for the unison and the octave. By definit ...
... As a consequence all intervals of any given type have the same size (e.g., all major thirds have the same size, all fifths have the same size, etc.). The price paid, in this case, is that none of them is justly tuned and perfectly consonant, except, of course, for the unison and the octave. By definit ...
CHAPTER 1 TONAL MODULATION WITH JUST
... (rounded off to the nearest tenth of a cent in the case of the Monophonic intervals) are used for both equal tempered intervals and Monophonic intervals as a unit of comparison.6 In the column for “Cents Deviation” the difference between the two versions is calculated. From this, one can see that th ...
... (rounded off to the nearest tenth of a cent in the case of the Monophonic intervals) are used for both equal tempered intervals and Monophonic intervals as a unit of comparison.6 In the column for “Cents Deviation” the difference between the two versions is calculated. From this, one can see that th ...
Musical Acoustics Interval, Scales, Tuning and Temperament
... by 9/8 (e.g., 32 /27 x 9 /8 = 4 /3 and 4 /3 x 9 /8 = 3/2). • Across the smaller intervals, the frequency must be multiplied by 256/243. In fact, 9/8 x 256/243 = 32/27, 27/16 x 256/243 = 16/9. • 9/8 = 1.125 = change of ~12% (whole tone) – W (“full step”) • 256/243 = 1.053 = change of ~5% (semitone ...
... by 9/8 (e.g., 32 /27 x 9 /8 = 4 /3 and 4 /3 x 9 /8 = 3/2). • Across the smaller intervals, the frequency must be multiplied by 256/243. In fact, 9/8 x 256/243 = 32/27, 27/16 x 256/243 = 16/9. • 9/8 = 1.125 = change of ~12% (whole tone) – W (“full step”) • 256/243 = 1.053 = change of ~5% (semitone ...
Music 181: Inversions of Intervals, Compound Intervals
... II. Compound intervals Any interval larger than an octave (8va) is a compound interval; intervals smaller than an octave are called simple intervals. Any compound interval can be reduced to a simple interval; in most musical contexts the compound interval and its simple counterpart are functionally ...
... II. Compound intervals Any interval larger than an octave (8va) is a compound interval; intervals smaller than an octave are called simple intervals. Any compound interval can be reduced to a simple interval; in most musical contexts the compound interval and its simple counterpart are functionally ...
L 8-‐9 Musical Scales, Chords , and Intervals, The Pythagorean and
... Each musical note has a perceived pitch with a parIcular frequency (the frequency of the fundamental) Going up or down in frequency, the perceived pitch follows a paXern One cycle of pitch repeIIon is called an ...
... Each musical note has a perceived pitch with a parIcular frequency (the frequency of the fundamental) Going up or down in frequency, the perceived pitch follows a paXern One cycle of pitch repeIIon is called an ...
Hearing Math and Seeing Music: a Workshop on Pitch Perception
... A is close to perfect, but the fifth from G# to D# is far too wide. A keyboard tuned in that system will sound beautiful in the key of D but terrible in the key of G#. If a composer didn’t care about writing in keys that would use the G# to D# fifth, they wouldn’t mind using the temperament. As comp ...
... A is close to perfect, but the fifth from G# to D# is far too wide. A keyboard tuned in that system will sound beautiful in the key of D but terrible in the key of G#. If a composer didn’t care about writing in keys that would use the G# to D# fifth, they wouldn’t mind using the temperament. As comp ...
LucyTuning*LucyScaleDevelopments*LucyTuned Lullabies*Pi
... A. LucyTuning uses a better physical and mathematical model for mapping harmonic relationships. This model is a dynamic three dimensional spiral instead of the traditional two dimensional static sine wave, and shows that harmonics beat at low frequencies. Q. Are any notes tuned the same as 12tET? A. ...
... A. LucyTuning uses a better physical and mathematical model for mapping harmonic relationships. This model is a dynamic three dimensional spiral instead of the traditional two dimensional static sine wave, and shows that harmonics beat at low frequencies. Q. Are any notes tuned the same as 12tET? A. ...
Why are pianos out of tune?
... To get around these problems, a number of different scales were proposed. One was mean-tone, in which the major third was taken as the basic feature. (Notice that three major thirds of four semitones each make up an octave of twelve semitones - C to E, E to G#, and G# (or Ab) to C.) This means that ...
... To get around these problems, a number of different scales were proposed. One was mean-tone, in which the major third was taken as the basic feature. (Notice that three major thirds of four semitones each make up an octave of twelve semitones - C to E, E to G#, and G# (or Ab) to C.) This means that ...
Tuning and Temperament
... Three successive pure major thirds don’t make an octave, in fact the C we arrived at is flat by 42% of a semitone, almost half way between B and C. If we use the ratios from the harmonic series we clearly have a big problem in building a scale, we can’t even get the octaves to come out correctly. We ...
... Three successive pure major thirds don’t make an octave, in fact the C we arrived at is flat by 42% of a semitone, almost half way between B and C. If we use the ratios from the harmonic series we clearly have a big problem in building a scale, we can’t even get the octaves to come out correctly. We ...
Music of Ancient Greece (ca. 7 Century B.C.E. – 476 C.E.)
... Musical intervals and intonation (tuning) were derived from Pythagoras. Pythagoras derived scales by tuning successive perfect, or pure fifths and bringing the frequencies down within the same octave. He figured this out mathematically, and gave birth to what is called “Pythagorean Intonation.” Pyth ...
... Musical intervals and intonation (tuning) were derived from Pythagoras. Pythagoras derived scales by tuning successive perfect, or pure fifths and bringing the frequencies down within the same octave. He figured this out mathematically, and gave birth to what is called “Pythagorean Intonation.” Pyth ...
Lecture Set 07
... Recall that men and women, singing the “same tone” together, tend to sing an OCTAVE apart. Our scale now has “two” notes. A little shabby! ...
... Recall that men and women, singing the “same tone” together, tend to sing an OCTAVE apart. Our scale now has “two” notes. A little shabby! ...
Musical Intervals and Scales
... • Step 2 - bring into the range of a single octave by descending in whole octave steps ...
... • Step 2 - bring into the range of a single octave by descending in whole octave steps ...
Scales - University of Rochester
... Pythagorean tuning, as a chain of perfect fifths, but in a meantone, each fifth is narrowed in order to make the other intervals like the major third closer to their ideal or perfect just ratios. Quarter-comma meantone is the most well known type of meantone temperament, and the term meantone temper ...
... Pythagorean tuning, as a chain of perfect fifths, but in a meantone, each fifth is narrowed in order to make the other intervals like the major third closer to their ideal or perfect just ratios. Quarter-comma meantone is the most well known type of meantone temperament, and the term meantone temper ...