Music 11, 7/10/06 Scales/Intervals We already know half steps and
... We already know half steps and whole steps (semitones and tones). We call these “seconds.” Adjacent pitch names are always called seconds, but because the space between adjacent pitch names can vary, there are different types of second: Major second (M2) = whole step = whole tone Minor second (m2) = ...
... We already know half steps and whole steps (semitones and tones). We call these “seconds.” Adjacent pitch names are always called seconds, but because the space between adjacent pitch names can vary, there are different types of second: Major second (M2) = whole step = whole tone Minor second (m2) = ...
notes and equations
... An interval is a ratio between two frequencies. The interval between two musical tones is the ratio between their fundamental frequencies. A perfect interval is the ratio between two small integers (typically below 6). Commonly used perfect intervals are: name unison octave minor third major third f ...
... An interval is a ratio between two frequencies. The interval between two musical tones is the ratio between their fundamental frequencies. A perfect interval is the ratio between two small integers (typically below 6). Commonly used perfect intervals are: name unison octave minor third major third f ...
intervals and scales
... key and an adjacent black piano key. You’ll also notice that there is no black note between E and F or between B and C, so the interval between those notes is also a semitone. A whole tone is two semitones: examples are C to D, D to E, F to G, G to A and A to B (there is a black note between each of ...
... key and an adjacent black piano key. You’ll also notice that there is no black note between E and F or between B and C, so the interval between those notes is also a semitone. A whole tone is two semitones: examples are C to D, D to E, F to G, G to A and A to B (there is a black note between each of ...
`frequency`. - Programma LLP
... second ‘dissonant’? Notice how in the first graphic there is a repeating pattern: every 3rd wave of the G matches up with every 2nd wave of the C (and in the second graphic how there is no pattern). This is the secret for creating pleasing sounding note combinations: Frequencies that match up at reg ...
... second ‘dissonant’? Notice how in the first graphic there is a repeating pattern: every 3rd wave of the G matches up with every 2nd wave of the C (and in the second graphic how there is no pattern). This is the secret for creating pleasing sounding note combinations: Frequencies that match up at reg ...
Music 181: Structure of the Major Scale
... Half Step; Half Tone; Semitone: Used generically for any interval that can be represented by two adjacent keys on the piano. Whole Tone; Whole Step: Used generically for any interval made up of two half steps. Whole tones are separated by one key on piano. ...
... Half Step; Half Tone; Semitone: Used generically for any interval that can be represented by two adjacent keys on the piano. Whole Tone; Whole Step: Used generically for any interval made up of two half steps. Whole tones are separated by one key on piano. ...
Modern Western Tuning System - Digital Commons @ Kent State
... perfect fifth, while 2:1 or 1:2 represent an ascending or descending octave. In order to create a 12-tone chromatic scale Pythagoras had to omit the Gb (which is supposed to be the same note as F#, however this tuning produces two different frequency rations for these notes) only using the 12 remain ...
... perfect fifth, while 2:1 or 1:2 represent an ascending or descending octave. In order to create a 12-tone chromatic scale Pythagoras had to omit the Gb (which is supposed to be the same note as F#, however this tuning produces two different frequency rations for these notes) only using the 12 remain ...
MSP_lecture3
... Construct as a geometric series - successive multiplication by 1.5 How many intervals to create – e.g., how to divide up the octave? Answer = 12 and still holds true today (for western music anyway) Interesting that we don’t use his system anymore but standardized on 12 ...
... Construct as a geometric series - successive multiplication by 1.5 How many intervals to create – e.g., how to divide up the octave? Answer = 12 and still holds true today (for western music anyway) Interesting that we don’t use his system anymore but standardized on 12 ...
Musical Interval and Ratio
... ‘The distance between two notes, measured as the ratio of their pitches, is called an interval. If the interval between two notes is a ratio of small integers (such as 2/1,3/2, or 4/3), they sound good together - they are consonant rather than dissonant. The pure intervals smaller than or equal to a ...
... ‘The distance between two notes, measured as the ratio of their pitches, is called an interval. If the interval between two notes is a ratio of small integers (such as 2/1,3/2, or 4/3), they sound good together - they are consonant rather than dissonant. The pure intervals smaller than or equal to a ...
Perfect Intervals
... the distance of an interval is one part of its name, but there’s more: every interval has another quality to it, which we’ll call inflection. inflection is a bit harder to understand, partly because some theorists use it depends on the type of interval. so let’s start by the term quality for looking ...
... the distance of an interval is one part of its name, but there’s more: every interval has another quality to it, which we’ll call inflection. inflection is a bit harder to understand, partly because some theorists use it depends on the type of interval. so let’s start by the term quality for looking ...
Chapter 15 - SFA Physics and Astronomy
... tones (even in dead rooms) so long as the tones are sounded close in time. Setting intervals for pure sinusoids (no partials) is difficult if the loudness is small enough to avoid exciting room modes. At high loudness levels there are enough harmonics generated in the room and ear to permit good ...
... tones (even in dead rooms) so long as the tones are sounded close in time. Setting intervals for pure sinusoids (no partials) is difficult if the loudness is small enough to avoid exciting room modes. At high loudness levels there are enough harmonics generated in the room and ear to permit good ...
Lecture 14a: Additional Remarks on Tuning Systems In previous
... Similarly, one can base a 31-note scale on approximating the meantone fifth 5^(1/4). 2. Expanding Just Intonation Another route that leads to an increased number of notes in the octave is to allow rational ratios involving prime factors greater than 5. (Recall that just intonation involves multiples ...
... Similarly, one can base a 31-note scale on approximating the meantone fifth 5^(1/4). 2. Expanding Just Intonation Another route that leads to an increased number of notes in the octave is to allow rational ratios involving prime factors greater than 5. (Recall that just intonation involves multiples ...
Music Fundamentals – Quiz 1 Review Pitch and Intervals Identify the
... the treble clef and the bottom space for those in the bass clef; the first example is completed for you. ...
... the treble clef and the bottom space for those in the bass clef; the first example is completed for you. ...
The Pythagorean Comma The Spiral of Fifths and Equal Temperament
... Counting up by seven octaves (ratios of 2/1) from C 32.7 Hz winds up at C 4185.6 Hz but counting up by twelve fifths (ratios of 3/2) yields C 4242.7 Hz. This discrepancy is known as the Pythagorean Comma and has been a powerful challenge for instrument makers and tuners. Fixed note instruments like ...
... Counting up by seven octaves (ratios of 2/1) from C 32.7 Hz winds up at C 4185.6 Hz but counting up by twelve fifths (ratios of 3/2) yields C 4242.7 Hz. This discrepancy is known as the Pythagorean Comma and has been a powerful challenge for instrument makers and tuners. Fixed note instruments like ...
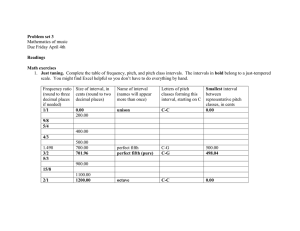
hw3
... a. Label the lines on the scale generation template attached with fractions representing the frequency ratios in just tuning. b. Which interval is worst approximated (in cents) by an equally tempered interval? Other than the octave, which is best approximated? c. How many pure fifths are there in th ...
... a. Label the lines on the scale generation template attached with fractions representing the frequency ratios in just tuning. b. Which interval is worst approximated (in cents) by an equally tempered interval? Other than the octave, which is best approximated? c. How many pure fifths are there in th ...
On Ben Johnston`s Notation and the Performance
... and thirds. In his book he uses the conventional note-names to represent a series of perfect fifths. So, for example, the common open strings are written conventionally as C - G - D - A - E. To make a simple consonant interval with C and G (thereby completing a triad tuned in the proportion 4:5:6) E ...
... and thirds. In his book he uses the conventional note-names to represent a series of perfect fifths. So, for example, the common open strings are written conventionally as C - G - D - A - E. To make a simple consonant interval with C and G (thereby completing a triad tuned in the proportion 4:5:6) E ...
“Tuning and temperament” by Rudolph Rasch Know who and where
... ¶1 Now you can see why Glarean used 24 × 36 for his full string: it makes it easy to find several Pythagorean (3:2) fifths. ¶2 “Sharps do not have a place . . . .”: In Pythagorean tuning, enharmonic spelling makes a big difference. Find the number corresponding to B on Glarean's chart. Use some math ...
... ¶1 Now you can see why Glarean used 24 × 36 for his full string: it makes it easy to find several Pythagorean (3:2) fifths. ¶2 “Sharps do not have a place . . . .”: In Pythagorean tuning, enharmonic spelling makes a big difference. Find the number corresponding to B on Glarean's chart. Use some math ...
Higher Music Literacy Unit 4 – Intervals
... To calculate the size of an interval whether visually or aurally, treat the lower note a ‘1’ and go up by step until the upper note is reached. ...
... To calculate the size of an interval whether visually or aurally, treat the lower note a ‘1’ and go up by step until the upper note is reached. ...
Music 170 Homework problem set 6 (due Nov. 3) 1. Two pipes, both
... successive harmonics (first an octave, then a fifth, and so on.) Which is the first of these intervals that is less than a tempered whole tone? A tempered semitone? 4. In the just scale (Rossing page 179), C to E is a perfect major third and E to G is a perfect minor third. What other intervals aris ...
... successive harmonics (first an octave, then a fifth, and so on.) Which is the first of these intervals that is less than a tempered whole tone? A tempered semitone? 4. In the just scale (Rossing page 179), C to E is a perfect major third and E to G is a perfect minor third. What other intervals aris ...
cents
... A major diatonic scale has (the 8th would be an The intervals are not all semitones some are whole tone is about a factor of (1.06)2 = 1.12 ...
... A major diatonic scale has (the 8th would be an The intervals are not all semitones some are whole tone is about a factor of (1.06)2 = 1.12 ...
presentation source
... • equal musical intervals - equal frequency ratio • 44on a “multiplicative” number line (=log scale) equal ratios are equidistant • advantage: in graphs below equal intervals have same length ...
... • equal musical intervals - equal frequency ratio • 44on a “multiplicative” number line (=log scale) equal ratios are equidistant • advantage: in graphs below equal intervals have same length ...
MSP_lecture10
... Transitional attempt to create a transposable scale based on simple integer ratios ...
... Transitional attempt to create a transposable scale based on simple integer ratios ...
Scales, Voice
... Octave interval is simple ratio Fifth is a simple ratio Fourth is a simple ratio Major third is a simple ratio Minor third is a simple ratio ...
... Octave interval is simple ratio Fifth is a simple ratio Fourth is a simple ratio Major third is a simple ratio Minor third is a simple ratio ...
Music Theory 171 Questions on Chapters 3A, 3B and 3C 3A
... 2. What does this say about the relationship between the fifth, the fourth and the octave? 3. What is created between the fifth and the fourth, and what is its ratio? 4. The notes of the major, minor, Phrygian and Middle Eastern tetrachords and listed on this page. Transpose them to the key of D and ...
... 2. What does this say about the relationship between the fifth, the fourth and the octave? 3. What is created between the fifth and the fourth, and what is its ratio? 4. The notes of the major, minor, Phrygian and Middle Eastern tetrachords and listed on this page. Transpose them to the key of D and ...