documentation dates
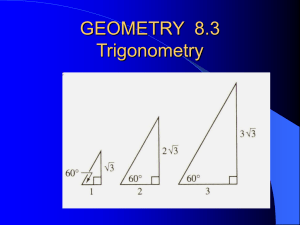
... problems and to prove relationships in geometric figures. [G-SRT5] Use trigonometric ratios and the Pythagorean Theorem to solve right triangles in applied problems. [G-SRT8] Apply geometric methods to solve design problems (e.g., designing an object or structure to satisfy physical constraints or m ...
... problems and to prove relationships in geometric figures. [G-SRT5] Use trigonometric ratios and the Pythagorean Theorem to solve right triangles in applied problems. [G-SRT8] Apply geometric methods to solve design problems (e.g., designing an object or structure to satisfy physical constraints or m ...
Heron`s Formula for Triangular Area
... If AHBO is a quadrilateral with diagonals AB and OH, then if ∠ HOB and ∠HAB are right angles (as shown), then a circle can be drawn passing through the vertices A, O, B, and H. ...
... If AHBO is a quadrilateral with diagonals AB and OH, then if ∠ HOB and ∠HAB are right angles (as shown), then a circle can be drawn passing through the vertices A, O, B, and H. ...
Geometry Pre-AP
... A geometry student concluded the statement shown. Supplementary angles form a linear pair. Which diagram can be used as a counterexample to this student’s conclusion? ...
... A geometry student concluded the statement shown. Supplementary angles form a linear pair. Which diagram can be used as a counterexample to this student’s conclusion? ...
2D Geometry Points, Distances, and Directions
... Rotations are another fundamental concept of 2D computational geometry. The good news is that only one rotation, the left rotation by 90 degrees, needs to be used very often. Nevertheless, understanding rotations is the easy way to understand other concepts such as the scalar product of vectors defin ...
... Rotations are another fundamental concept of 2D computational geometry. The good news is that only one rotation, the left rotation by 90 degrees, needs to be used very often. Nevertheless, understanding rotations is the easy way to understand other concepts such as the scalar product of vectors defin ...
Analytic geometry
In classical mathematics, analytic geometry, also known as coordinate geometry, or Cartesian geometry, is the study of geometry using a coordinate system. This contrasts with synthetic geometry.Analytic geometry is widely used in physics and engineering, and is the foundation of most modern fields of geometry, including algebraic, differential, discrete and computational geometry.Usually the Cartesian coordinate system is applied to manipulate equations for planes, straight lines, and squares, often in two and sometimes in three dimensions. Geometrically, one studies the Euclidean plane (two dimensions) and Euclidean space (three dimensions). As taught in school books, analytic geometry can be explained more simply: it is concerned with defining and representing geometrical shapes in a numerical way and extracting numerical information from shapes' numerical definitions and representations. The numerical output, however, might also be a vector or a shape. That the algebra of the real numbers can be employed to yield results about the linear continuum of geometry relies on the Cantor–Dedekind axiom.