Download Study Guide - Quadrilaterals

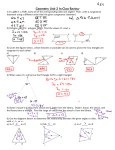
Study Guide - Quadrilaterals
Our minimal definition of square states that “square is a quadrilateral with 4 congruent sides and one
right angle”. Clearly explain (or prove) that this definition implies that all angles have to be right angles.
Construction of quadrilaterals
You should be able to construct quadrilaterals (kite, trapezoid, isosceles trapezoid, parallelogram,
rhombus, rectangle, square) given their minimal definitions (you do not have to memorize the
definitions, they will be provided). Make sure your object is not over- or under- constrained.
Properties of Quadrilaterals
You should be able to discuss properties of quadrilaterals (see the chart). Keep in mind that these
properties must hold for ALL shapes included in the category. If a property does not hold for a given
quadrilateral, make sure you provide a counterexample. If it holds, briefly justify your answer by only
assuming things that are to the left of the box you are working on. On the test you will be told what you
can or cannot assume.
Below are examples of possible questions. Make sure you are comfortable with all properties we
discussed in class.
1. Kite: a quadrilateral with two distinct pairs of adjacent congruent sides.
a. Our minimal definition of a kite involves the word distinct (“distinct pairs of adjacent
congruent sides”). Explain why it is necessary there.
b. Q: Are the diagonals always perpendicular? (You may assume that one diagonal bisects the
other.)
c. Q2: Are the diagonals bisecting each other? Is one bisected by the other? (You may
assume that “2 pairs of adjacent sides are congruent”, and “1 pair of opposite
angles are congruent”.)
b. Justify the formula for the area of a kite (diagonals are known).
2. Trapezoid: a quadrilateral with at least one pair of parallel sides.
a. We talked about two different definitions of a trapezoid (we referred to them as “modern”
and “traditional”). Discuss the differences and explain why the “modern” definition is
becoming a preferred way to define a trapezoid.
b. Q: Certain pairs of adjacent angles have a special property. What is the property and which
angles does it apply to? Label the angles to be able to refer to them in your answer.
c. Q2: Diagonals split a trapezoid into 4 non-overlapping triangles. Among those 4 triangles,
there is one pair of similar triangles. Identify the two and explain why they are similar. The
other two triangles also share a certain property. What is it and why does it hold? Label the
triangles to be able to refer to them in your answer.
d. Justify the formula for the area of a trapezoid by knowing the triangle area formula.
d. Explain how can the following picture be used to derive the formula
of a trapezoid.
 Explain why it is possible to arrange two copies
of a trapezoid like this (hint – look for
supplementary angles).
 Explain how this arrangement helps derive the
3.
4.
5.
6.
7.
area formula.
Isosceles trapezoid: a trapezoid with one pair of congruent base angles.
a. Prove that diagonals are congruent. You may assume that the legs of isosceles trapezoid
are congruent and angles in the definition are congruent.
b. Prove that among 4 non-overlapping triangles created by diagonals, there is one pair of
similar and one pair of congruent triangles. You may assume that diagonals are
congruent, the legs of isosceles trapezoid are congruent and angles in the definition are
congruent.
Parallelogram: a quadrilateral with two pairs of parallel sides.
a. Q: Are the diagonals congruent? (Do not assume the diagonals are perpendicular to each
other nor that they bisect one another.)
b. Q2: Are the diagonals perpendicular to each other?
c. Q3: Are the diagonals bisecting each other?
d. Q4: Is there another property of diagonals worth mentioning?
e. Justify the formula for the area of a parallelogram.
Rhombus: a quadrilateral with four congruent sides.
a. Q: Are the diagonals congruent? (Do not assume the diagonals are perpendicular to each
other nor that they bisect one another.)
b. Q2: Are the diagonals perpendicular to each other? (You may assume diagonals are
congruent and bisect each other).
c. Q3: Are the diagonals bisecting each other? (Do not assume the diagonals are perpendicular
to each other.)
d. Q4: Diagonals split the rhombus into 4 triangles. They all share certain properties. Name and
justify at least one such property.
e. Prove that a rhombus is a parallelogram. Use only triangle congruence theorems, Isosceles
Triangle Theorem and theorems about angles created by two parallel lines cut by a
transversal.
Rectangle: a quadrilateral with three right angles.
a. Q: Specify two properties of the diagonals and prove them.
Square: a quadrilateral with four congruent sides and one right angle.
a. Q: What might be an alternate formula for the area of a square that does not involve the
side(s) of the square? (See if square is a kite.)
8. Randomly select a few boxes and provide a justification in a similar manner.
9. Find the sum of the measures of all interior angles of a quadrilateral
10. Areas of figures. You should be able to find the areas of shapes that can be broken
down into known quadrilaterals and triangles. In the pictures below, do not assume
that a shape is a trapezoid or square (etc.) just because it looks like one. Make sure
that you have convincing arguments why you are considering the given shape a
trapezoid or square (etc.)
(Bold lines indicate line segments to which the measures refer. “Double arrow”
indicates parallel sides.)
Hierarchy of Quadrilaterals. You should be able to generate the hierarchy and use it
to answer the following questions:
11. Does the area formula for a kite work for a rhombus? (Alternative wording: can you
use the formula
(where d1 and d2 are the lengths of diagonals) to calculate
the area of a rhombus?
12. A student says: “The formula for the area of a rectangle is just a special case of the
formula for the area of a trapezoid.” . Is the student right? Explain.
13. We know that the diagonals of a kite are perpendicular to each other. Knowing this,
can we say anything about the diagonals of a square?