An Introduction to Crystal Physics
... with a tensor which establishes the relation existing between measurable physical tensor quantities. Every scalar is a zero-rank, and every vector a first-rank tensor. Generally in crystal physics a set of 3 r quantities with r indices transforming under transition from the old coordinates to the ne ...
... with a tensor which establishes the relation existing between measurable physical tensor quantities. Every scalar is a zero-rank, and every vector a first-rank tensor. Generally in crystal physics a set of 3 r quantities with r indices transforming under transition from the old coordinates to the ne ...
43.1 Vector Fields and their properties
... Limit and continuity of vector-fields behave in a fashion similar to that of scalar fields (see theorem 29.2.1). We shall assume (without proof) that vector- fields also have similar properties. We can also define differentiability and existence of partial derivatives for vector fields via their com ...
... Limit and continuity of vector-fields behave in a fashion similar to that of scalar fields (see theorem 29.2.1). We shall assume (without proof) that vector- fields also have similar properties. We can also define differentiability and existence of partial derivatives for vector fields via their com ...
Lecture 1 Linear Superalgebra
... Definition 5.2. If M is an A-module, then GL(M) is defined as the group of automorphisms of M and we call it the super general linear group of automorphisms of M. If M = Ap|q the free A-module generated by p even and q odd variables, then we write GL(M) = GLp|q (A). We may also use the notation GLp| ...
... Definition 5.2. If M is an A-module, then GL(M) is defined as the group of automorphisms of M and we call it the super general linear group of automorphisms of M. If M = Ap|q the free A-module generated by p even and q odd variables, then we write GL(M) = GLp|q (A). We may also use the notation GLp| ...
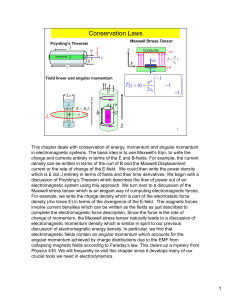
This chapter deals with conservation of energy, momentum and
... points in the phi-hat direction. We then form the cross product of E and B to get a Poynting vector which points in the –s-hat direction. This is a bit surprising since one would naively think the power flows into the ends rather than into the resistor through the cylinder walls. We next compute the ...
... points in the phi-hat direction. We then form the cross product of E and B to get a Poynting vector which points in the –s-hat direction. This is a bit surprising since one would naively think the power flows into the ends rather than into the resistor through the cylinder walls. We next compute the ...
calculusreview3
... KAAP686 Mathematics and Signal Processing for Biomechanics Calculus review 3 Vectors in space 1. Vectors Magnitude & direction Examples: pos., veloc., accel., force, Scalar: a number, with no directionality; a one-dimensional vector. Special unit direction vectors i, j, k point in positive direction ...
... KAAP686 Mathematics and Signal Processing for Biomechanics Calculus review 3 Vectors in space 1. Vectors Magnitude & direction Examples: pos., veloc., accel., force, Scalar: a number, with no directionality; a one-dimensional vector. Special unit direction vectors i, j, k point in positive direction ...