Semiclassical calculation of electron spectra in atoms through two
... Coulomb potential leads to the lift of the degeneracy in the orbital momentum l . It has been shown in [1], that the corresponding splitting E nl E nl E n 0 quadratically depends on the orbital momentum l 1/ 2 (here n is a principal quantum number). In addition an analysis of the energy l ...
... Coulomb potential leads to the lift of the degeneracy in the orbital momentum l . It has been shown in [1], that the corresponding splitting E nl E nl E n 0 quadratically depends on the orbital momentum l 1/ 2 (here n is a principal quantum number). In addition an analysis of the energy l ...
Statistical Thermodynamics
... • The most “disordered” macrostate is the state with the highest probability. • The macrostate with the highest thermodynamic probability will be the observed equilibrium state of the system. • The statistical model suggests that systems tend to change spontaneously from states with low thermodynam ...
... • The most “disordered” macrostate is the state with the highest probability. • The macrostate with the highest thermodynamic probability will be the observed equilibrium state of the system. • The statistical model suggests that systems tend to change spontaneously from states with low thermodynam ...
Quantum Mechanics
... Some folks think “measurement” means “a conscious observer observes”, but QM is NOT precise about what a measurement is. If measurement requires a conscious observer, you get odd things, like Schroedinger’s Cat. There are almost no restrictions on what an arbitrary wavefunction looks like. (Must be ...
... Some folks think “measurement” means “a conscious observer observes”, but QM is NOT precise about what a measurement is. If measurement requires a conscious observer, you get odd things, like Schroedinger’s Cat. There are almost no restrictions on what an arbitrary wavefunction looks like. (Must be ...
Chapter 8 - Bakersfield College
... A. The Niels Bohr model of the atom, proposed in 1913, suggested that an electron in an atom possesses a specific energy level that is dependent on the orbit it is in. An electron in the innermost orbit has the least energy. B. Electron orbits are identified by a quantum number n, and each orbit cor ...
... A. The Niels Bohr model of the atom, proposed in 1913, suggested that an electron in an atom possesses a specific energy level that is dependent on the orbit it is in. An electron in the innermost orbit has the least energy. B. Electron orbits are identified by a quantum number n, and each orbit cor ...
l - Evergreen
... * write down boundary conditions (BC) * think about what form of y(x) will fit the potential * find the wavenumbers kn=2 / * find the allowed energies En * sub k into y(x) and normalize to find the amplitude A * Now you know everything about a QM system in this potential, and you can calculate for ...
... * write down boundary conditions (BC) * think about what form of y(x) will fit the potential * find the wavenumbers kn=2 / * find the allowed energies En * sub k into y(x) and normalize to find the amplitude A * Now you know everything about a QM system in this potential, and you can calculate for ...
Quantum Theory
... Wave theory of light said that any frequency of light should have worked This led to the concept of light as a particle ...
... Wave theory of light said that any frequency of light should have worked This led to the concept of light as a particle ...
Problem set 6
... 1. Consider a free non-relativistic particle of mass m. In the lecture we assumed the time evolution of each Fourier component of a matter wave ψ(x, t) was given by ei(kx−ω(k)t) corresponding to a right moving wave if k, ω(k) were of the same sign. We could equally well have considered the time evol ...
... 1. Consider a free non-relativistic particle of mass m. In the lecture we assumed the time evolution of each Fourier component of a matter wave ψ(x, t) was given by ei(kx−ω(k)t) corresponding to a right moving wave if k, ω(k) were of the same sign. We could equally well have considered the time evol ...
Section 13.2 - CPO Science
... • In the current model of the atom, we think of the electrons in an atom as moving around the nucleus in an area called an electron cloud. • The energy levels occur because electrons in the cloud are at different average distances from the nucleus. ...
... • In the current model of the atom, we think of the electrons in an atom as moving around the nucleus in an area called an electron cloud. • The energy levels occur because electrons in the cloud are at different average distances from the nucleus. ...
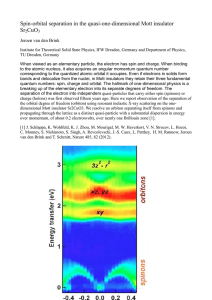
Spin-orbital separation in the quasi-one
... When viewed as an elementary particle, the electron has spin and charge. When binding to the atomic nucleus, it also acquires an angular momentum quantum number corresponding to the quantized atomic orbital it occupies. Even if electrons in solids form bands and delocalize from the nuclei, in Mott i ...
... When viewed as an elementary particle, the electron has spin and charge. When binding to the atomic nucleus, it also acquires an angular momentum quantum number corresponding to the quantized atomic orbital it occupies. Even if electrons in solids form bands and delocalize from the nuclei, in Mott i ...
PX408: Relativistic Quantum Mechanics Tim Gershon ()
... • PX148 Classical Mechanics & Relativity • PX262 Quantum Mechanics and its Applications Additional experience in quantum physics would be useful, for example from the following modules: • PX101 Quantum Phenomena • PX382 Quantum Physics of Atoms Basic (PX147, PX274) or more advanced (PX395, PX445) kn ...
... • PX148 Classical Mechanics & Relativity • PX262 Quantum Mechanics and its Applications Additional experience in quantum physics would be useful, for example from the following modules: • PX101 Quantum Phenomena • PX382 Quantum Physics of Atoms Basic (PX147, PX274) or more advanced (PX395, PX445) kn ...
Particle in a box

In quantum mechanics, the particle in a box model (also known as the infinite potential well or the infinite square well) describes a particle free to move in a small space surrounded by impenetrable barriers. The model is mainly used as a hypothetical example to illustrate the differences between classical and quantum systems. In classical systems, for example a ball trapped inside a large box, the particle can move at any speed within the box and it is no more likely to be found at one position than another. However, when the well becomes very narrow (on the scale of a few nanometers), quantum effects become important. The particle may only occupy certain positive energy levels. Likewise, it can never have zero energy, meaning that the particle can never ""sit still"". Additionally, it is more likely to be found at certain positions than at others, depending on its energy level. The particle may never be detected at certain positions, known as spatial nodes.The particle in a box model provides one of the very few problems in quantum mechanics which can be solved analytically, without approximations. This means that the observable properties of the particle (such as its energy and position) are related to the mass of the particle and the width of the well by simple mathematical expressions. Due to its simplicity, the model allows insight into quantum effects without the need for complicated mathematics. It is one of the first quantum mechanics problems taught in undergraduate physics courses, and it is commonly used as an approximation for more complicated quantum systems.