The world of Atoms - University of California, Irvine
... - electron orbits around the nucleus like a wave - orbit is described by wavefunction - wavefunction is discrete solution of wave equation - only certain orbits are allowed - orbits correspond to energy levels of atom Niels Bohr (1885-1962) ...
... - electron orbits around the nucleus like a wave - orbit is described by wavefunction - wavefunction is discrete solution of wave equation - only certain orbits are allowed - orbits correspond to energy levels of atom Niels Bohr (1885-1962) ...
Solved Problems on Quantum Mechanics in One
... Eq. (44) are equations for the allowed values of k. The equation with the positive sign yields values of θ in the first quadrant. The equation with the negative sign yields values of θ in the third quadrant. Solving Eq. (44) numerically for an electron in a well with U = 5 eV and L = 100 pm yields t ...
... Eq. (44) are equations for the allowed values of k. The equation with the positive sign yields values of θ in the first quadrant. The equation with the negative sign yields values of θ in the third quadrant. Solving Eq. (44) numerically for an electron in a well with U = 5 eV and L = 100 pm yields t ...
Lecture 13: Heisenberg and Uncertainty
... Quantum Mechanics The observer is not objective and passive The act of observation changes the physical system irrevocably This is known as subjective reality ...
... Quantum Mechanics The observer is not objective and passive The act of observation changes the physical system irrevocably This is known as subjective reality ...
Quantum Numbers
... • Ground state: An atom’s lowest energy state • Excited state: Higher potential energy than ground state. • Photon: A particle of electromagnetic radiation having zero mass and carrying a quantum of energy (i.e., packet of light) • Only certain wavelengths of light are emitted by hydrogen atoms when ...
... • Ground state: An atom’s lowest energy state • Excited state: Higher potential energy than ground state. • Photon: A particle of electromagnetic radiation having zero mass and carrying a quantum of energy (i.e., packet of light) • Only certain wavelengths of light are emitted by hydrogen atoms when ...
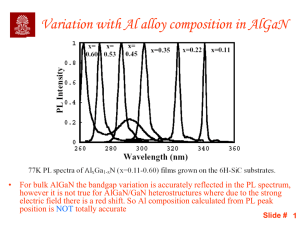
Slide 1
... • For bulk AlGaN the bandgap variation is accurately reflected in the PL spectrum, however it is not true for AlGaN/GaN heterostructures where due to the strong electric field there is a red shift. So Al composition calculated from PL peak position is NOT totally accurate ...
... • For bulk AlGaN the bandgap variation is accurately reflected in the PL spectrum, however it is not true for AlGaN/GaN heterostructures where due to the strong electric field there is a red shift. So Al composition calculated from PL peak position is NOT totally accurate ...
WAVE MECHANICS (Schrödinger, 1926)
... * The energy depends only on the principal quantum number, as in the Bohr model: En = -2.179 X 10-18J /n2 * The orbitals are named by giving the n value followed by a letter symbol for l: l= 0,1, 2, 3, 4, 5, ... s p d f g h ... * All orbitals with the same n are called a “shell”. All orbitals with t ...
... * The energy depends only on the principal quantum number, as in the Bohr model: En = -2.179 X 10-18J /n2 * The orbitals are named by giving the n value followed by a letter symbol for l: l= 0,1, 2, 3, 4, 5, ... s p d f g h ... * All orbitals with the same n are called a “shell”. All orbitals with t ...
|ket> and notation
... to one composed of wavefunctions. Instead of describing a physical system with coordinates and momenta, x and p (Dirac called them c-numbers), the quantum mechanical description is based on operators x and p (q-numbers) that operate on a wavefunction ψ. The wave function can be a function of coordin ...
... to one composed of wavefunctions. Instead of describing a physical system with coordinates and momenta, x and p (Dirac called them c-numbers), the quantum mechanical description is based on operators x and p (q-numbers) that operate on a wavefunction ψ. The wave function can be a function of coordin ...
Specialization: 010600/52 Program: Applied Mathematics and Physics Program director: prof. S.L. Yakovlev
... problem itself. The aim of the present work is to explore deal.II and to evaluate its efficiency, stability and accuracy for quantum mechanical problems. The helium atom with zero total angular momentum has been chosen as a benchmark of the three-body Coulomb problem. Both the exact threedimensional ...
... problem itself. The aim of the present work is to explore deal.II and to evaluate its efficiency, stability and accuracy for quantum mechanical problems. The helium atom with zero total angular momentum has been chosen as a benchmark of the three-body Coulomb problem. Both the exact threedimensional ...
Lecture 9
... = - ħ2 ∫ (2/L)1/2 sin(nπx/L) exp(iωt)
× (2/L)1/2 (d2/dx2) sin(nπx/L) exp(-iωt) dx
= - ħ2 (2/L) ∫ sin(nπx/L) (d2/dx2) sin(nπx/L) dx
= ħ2 (2/L) (nπ/L)2 ∫0L sin2(nπx/L) dx
= ħ2 (2/L) (nπ/L)2 (L/2)
= (ħ n π / L)2.
This may appear to be paradoxical at first: how can the average
momentum be zero, but ...
...
to the wave function
... • The probability to find the particle in the volume element d = dr dt located at r at time t is given by (r, t)(r, t) d . – Born interpretation ...
... • The probability to find the particle in the volume element d = dr dt located at r at time t is given by (r, t)(r, t) d . – Born interpretation ...
November 18
... Thurs 11/18 Review for Test Chapter 4 Know your E/M spectrum, from long wavelength/low frequency to short wavelength. High frequency 2 formulas C(speed of light 3x 108 m/s)=(lambda[wavelength in meters])(frequency in Hertz) Energy in Joules = h (plank’s constant 6.6 x 10-34) x frequency Example prob ...
... Thurs 11/18 Review for Test Chapter 4 Know your E/M spectrum, from long wavelength/low frequency to short wavelength. High frequency 2 formulas C(speed of light 3x 108 m/s)=(lambda[wavelength in meters])(frequency in Hertz) Energy in Joules = h (plank’s constant 6.6 x 10-34) x frequency Example prob ...
Does the Everyday World Really Obey Quantum Mechanics?
... PB or C = PB + PC + 2ABAC Suppose AC = ±AB, at random. Then average of PB or C is av. of AB AC PB or C = PB + PC + 2ABAC but ABAC = av. of +A2B and -A2B = 0 so PB or C =PB + PC “COMMON SENSE” RESULT, i.e.“as if” each system chose path B or path C WHEN AB AND AC SIMULTANEOUSLY “EXIST”, NEITHER B N ...
... PB or C = PB + PC + 2ABAC Suppose AC = ±AB, at random. Then average of PB or C is av. of AB AC PB or C = PB + PC + 2ABAC but ABAC = av. of +A2B and -A2B = 0 so PB or C =PB + PC “COMMON SENSE” RESULT, i.e.“as if” each system chose path B or path C WHEN AB AND AC SIMULTANEOUSLY “EXIST”, NEITHER B N ...
Particle in a box

In quantum mechanics, the particle in a box model (also known as the infinite potential well or the infinite square well) describes a particle free to move in a small space surrounded by impenetrable barriers. The model is mainly used as a hypothetical example to illustrate the differences between classical and quantum systems. In classical systems, for example a ball trapped inside a large box, the particle can move at any speed within the box and it is no more likely to be found at one position than another. However, when the well becomes very narrow (on the scale of a few nanometers), quantum effects become important. The particle may only occupy certain positive energy levels. Likewise, it can never have zero energy, meaning that the particle can never ""sit still"". Additionally, it is more likely to be found at certain positions than at others, depending on its energy level. The particle may never be detected at certain positions, known as spatial nodes.The particle in a box model provides one of the very few problems in quantum mechanics which can be solved analytically, without approximations. This means that the observable properties of the particle (such as its energy and position) are related to the mass of the particle and the width of the well by simple mathematical expressions. Due to its simplicity, the model allows insight into quantum effects without the need for complicated mathematics. It is one of the first quantum mechanics problems taught in undergraduate physics courses, and it is commonly used as an approximation for more complicated quantum systems.