S. Mayboroda:
... permeates acoustics, quantum physics, elasticity, to name just a few. Localization on fractal domains was used for noise abatement walls which up to date hold world efficiency record. Anderson localization of quantum states of electrons has become one of the prominent subjects in quantum physics, ha ...
... permeates acoustics, quantum physics, elasticity, to name just a few. Localization on fractal domains was used for noise abatement walls which up to date hold world efficiency record. Anderson localization of quantum states of electrons has become one of the prominent subjects in quantum physics, ha ...
Schrödinger`s equation
... Above is the 1-dimensional Schrödinger equation (for 3-dimension replace ∂ 2 /∂x2 by ∇2 and x by ~x). The Schrödinger equation (1) is a postulate of quantum mechanics. We can arrive at Schrödinger equation from a few reasonable assumptions, 1. the quantum mechanical wave equation must be consiste ...
... Above is the 1-dimensional Schrödinger equation (for 3-dimension replace ∂ 2 /∂x2 by ∇2 and x by ~x). The Schrödinger equation (1) is a postulate of quantum mechanics. We can arrive at Schrödinger equation from a few reasonable assumptions, 1. the quantum mechanical wave equation must be consiste ...
Objective A - TuHS Physics Homepage
... closest approach brings it to within 47 femtometers of a Gold nucleus. What is 2. An Alpha particle’s its energy in eV (Atomic number is 79, mass of an alpha is 6.644x10−27 kg, look up femto in your data packet) (4.8 MeV) 3. Chapter 27: 73(4.7E-14 m) Objective K: The Bohr Atom Problems: Chapter 2 ...
... closest approach brings it to within 47 femtometers of a Gold nucleus. What is 2. An Alpha particle’s its energy in eV (Atomic number is 79, mass of an alpha is 6.644x10−27 kg, look up femto in your data packet) (4.8 MeV) 3. Chapter 27: 73(4.7E-14 m) Objective K: The Bohr Atom Problems: Chapter 2 ...
Hybrid_Quantu_Classic_Dynamics!!
... Strengths of Hybrid Approach • Electronic and nuclear quantum effects included • Motion of complete solvated enzyme included • Enables calculation of rates and KIEs • Elucidates fundamental nature of nuclear quantum effects • Provides thermally averaged, equilibrium information • Provides real-time ...
... Strengths of Hybrid Approach • Electronic and nuclear quantum effects included • Motion of complete solvated enzyme included • Enables calculation of rates and KIEs • Elucidates fundamental nature of nuclear quantum effects • Provides thermally averaged, equilibrium information • Provides real-time ...
Tunneling Effect and Its Applications Quantum
... If we take derivative of the phase we get ...or we get another derivative of the phase as ...which can be rewritten using the concepts of energy and momentum ...
... If we take derivative of the phase we get ...or we get another derivative of the phase as ...which can be rewritten using the concepts of energy and momentum ...
Winterschool Obergurgl 2017
... theoretical models and in emerging experimental settings. The goal of this interdisciplinary school is to foster interaction between these communities. The school is aimed at PhD students and Postdocs who work in classical networks, quantum physics, quantum communication and quantum information; ...
... theoretical models and in emerging experimental settings. The goal of this interdisciplinary school is to foster interaction between these communities. The school is aimed at PhD students and Postdocs who work in classical networks, quantum physics, quantum communication and quantum information; ...
Atomic and Molecular Physics for Physicists Ben-Gurion University of the Negev
... angular momentum J, and as JZ=LZ+SZ, and as, when calculating the distances and therefore the forces one has to take into account that g for the orbital motion is gL=1 while for the spin is gS=2, we will have the following forces acting on the atoms: F(LZ=+1, SZ=+1/2), F(LZ=+0, SZ=+1/2), F(LZ=-1, SZ ...
... angular momentum J, and as JZ=LZ+SZ, and as, when calculating the distances and therefore the forces one has to take into account that g for the orbital motion is gL=1 while for the spin is gS=2, we will have the following forces acting on the atoms: F(LZ=+1, SZ=+1/2), F(LZ=+0, SZ=+1/2), F(LZ=-1, SZ ...
x - Piazza
... Time-Independent Schrödinger Wave Equation The potential in many cases will not depend explicitly on time: V = V(x). The Schrödinger equation’s dependence on time and position can then be separated. Let: ...
... Time-Independent Schrödinger Wave Equation The potential in many cases will not depend explicitly on time: V = V(x). The Schrödinger equation’s dependence on time and position can then be separated. Let: ...
particles - Prof.Dr.Ümit Demir
... depends on the space available for them. Thus, the properties of a material are characterized by a specific “length scale”, usually on the nm dimension. If the physical size of the material is reduced below this length scale, its properties change and become sensitive to size and shape. ...
... depends on the space available for them. Thus, the properties of a material are characterized by a specific “length scale”, usually on the nm dimension. If the physical size of the material is reduced below this length scale, its properties change and become sensitive to size and shape. ...
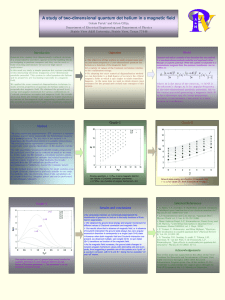
Exact diagonalization analysis of quantum dot helium for
... The exact numerical diagonalization (ED) method is a standard technique used to solve numerically the Schrödinger equation for a quantum system. The key idea of the method is to diagonalize the Hamiltonian matrix in a suitable chosen basis. The resulting matrix eigenvalues correspond to the numerica ...
... The exact numerical diagonalization (ED) method is a standard technique used to solve numerically the Schrödinger equation for a quantum system. The key idea of the method is to diagonalize the Hamiltonian matrix in a suitable chosen basis. The resulting matrix eigenvalues correspond to the numerica ...
Particle in a box

In quantum mechanics, the particle in a box model (also known as the infinite potential well or the infinite square well) describes a particle free to move in a small space surrounded by impenetrable barriers. The model is mainly used as a hypothetical example to illustrate the differences between classical and quantum systems. In classical systems, for example a ball trapped inside a large box, the particle can move at any speed within the box and it is no more likely to be found at one position than another. However, when the well becomes very narrow (on the scale of a few nanometers), quantum effects become important. The particle may only occupy certain positive energy levels. Likewise, it can never have zero energy, meaning that the particle can never ""sit still"". Additionally, it is more likely to be found at certain positions than at others, depending on its energy level. The particle may never be detected at certain positions, known as spatial nodes.The particle in a box model provides one of the very few problems in quantum mechanics which can be solved analytically, without approximations. This means that the observable properties of the particle (such as its energy and position) are related to the mass of the particle and the width of the well by simple mathematical expressions. Due to its simplicity, the model allows insight into quantum effects without the need for complicated mathematics. It is one of the first quantum mechanics problems taught in undergraduate physics courses, and it is commonly used as an approximation for more complicated quantum systems.