Midterm solutions - Bryn Mawr College
... (D) be essentially unaffected, since its main function--producing ordered work--is not dependent on disordered heat. Answer: (A) lose its ability to turn thermal energy into work. Why: As a heat engine, the car engine can only produce work out of heat by letting heat flow from hot to cold. If you sp ...
... (D) be essentially unaffected, since its main function--producing ordered work--is not dependent on disordered heat. Answer: (A) lose its ability to turn thermal energy into work. Why: As a heat engine, the car engine can only produce work out of heat by letting heat flow from hot to cold. If you sp ...
question 2 - Larbert High School
... change in momentum, average force exerted and time of contact. c) Apply the theory used above to explain why it is compulsory to wear a helmet when riding on a motorcycle. ...
... change in momentum, average force exerted and time of contact. c) Apply the theory used above to explain why it is compulsory to wear a helmet when riding on a motorcycle. ...
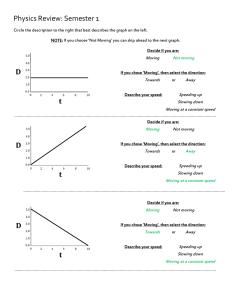
Motion in Two Dimensions
... Question: The graph below (not drawn to scale) shows the motion of tennis ball that was thrown vertically upwards from an open window some distance from the ground. It takes the ball 0,2 s to reach its highest point before falling back to the ground. Study the graph given and calculate 1. how high t ...
... Question: The graph below (not drawn to scale) shows the motion of tennis ball that was thrown vertically upwards from an open window some distance from the ground. It takes the ball 0,2 s to reach its highest point before falling back to the ground. Study the graph given and calculate 1. how high t ...
Physics I - Rose
... Solve: Only spring 2 touches the mass, so the net force on the mass is Fm F2 on m. Newton’s third law tells us that F2 on m Fm on 2 and that F2 on 1 F1 on 2. From Fnet ma, the net force on a massless spring is zero. Thus Fw on 1 F2 on 1 k1x1 and Fm on 2 F1 on 2 k2x2. Combining thes ...
... Solve: Only spring 2 touches the mass, so the net force on the mass is Fm F2 on m. Newton’s third law tells us that F2 on m Fm on 2 and that F2 on 1 F1 on 2. From Fnet ma, the net force on a massless spring is zero. Thus Fw on 1 F2 on 1 k1x1 and Fm on 2 F1 on 2 k2x2. Combining thes ...
Introduction to Classical Mechanics 1 HISTORY
... After the publication of Principia, Newton was the most renowned scientist in the world. His achievement was fully recognized during his lifetime. Today scientists and engineers still use Newton’s theory of mechanics. In the 20th century some limitations of Newtonian mechanics were discovered: Class ...
... After the publication of Principia, Newton was the most renowned scientist in the world. His achievement was fully recognized during his lifetime. Today scientists and engineers still use Newton’s theory of mechanics. In the 20th century some limitations of Newtonian mechanics were discovered: Class ...
Work and Energy combined
... Well, the law of conservation of energy always works – it is the law, after all. What happens is that the energy of the ball is transformed into energy forms that do not contribute to the bounce height. We call these transformations energy losses. They are not really energy losses, however, in the ...
... Well, the law of conservation of energy always works – it is the law, after all. What happens is that the energy of the ball is transformed into energy forms that do not contribute to the bounce height. We call these transformations energy losses. They are not really energy losses, however, in the ...
On the Theory of Quanta Louis-Victor de Broglie (1892-1987) P ARIS
... leads us to consider admitting that energy is entirely concentrated in small regions of space, if not even condensed at singularities. The principle of inertia of energy attributes to every body a proper mass (that is a mass as measured by an observer at rest with respect to it) of m0 and a proper e ...
... leads us to consider admitting that energy is entirely concentrated in small regions of space, if not even condensed at singularities. The principle of inertia of energy attributes to every body a proper mass (that is a mass as measured by an observer at rest with respect to it) of m0 and a proper e ...
Thin Rod Flexural Acoustic Wave Devices
... The basic arrangement for exciting and receiving thin rod flexural acoustic waves is shown in Fig.2. A 10.5 J.UI1 radius gold wire is fixed at two posts by adhesive tape. A piezoelectric longitudinal ultrasonic transducer is bonded at the end of a silica glass horn. The small displacements of the ul ...
... The basic arrangement for exciting and receiving thin rod flexural acoustic waves is shown in Fig.2. A 10.5 J.UI1 radius gold wire is fixed at two posts by adhesive tape. A piezoelectric longitudinal ultrasonic transducer is bonded at the end of a silica glass horn. The small displacements of the ul ...
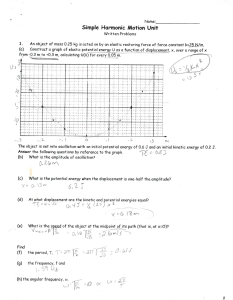
Simple harmonic Motion Answers
... A solid disk/of radius R = 12 em oscillates as a physical pendulum abaut an axis perpendicular to the plane of the disk at a distance r from its center. Calculate the period of oscillation when (a) r = R/2 and ...
... A solid disk/of radius R = 12 em oscillates as a physical pendulum abaut an axis perpendicular to the plane of the disk at a distance r from its center. Calculate the period of oscillation when (a) r = R/2 and ...