Vibration Dynamics
... in which, x is a column array of describing coordinates of the system, and f is a column array of the associated applied forces. The square matrices [m], [c], [k] are the mass, damping, and stiffness matrices. Example 30 (The one, two, and three DOF model of vehicles) The one, two, and three DOF mod ...
... in which, x is a column array of describing coordinates of the system, and f is a column array of the associated applied forces. The square matrices [m], [c], [k] are the mass, damping, and stiffness matrices. Example 30 (The one, two, and three DOF model of vehicles) The one, two, and three DOF mod ...
Gravity
... Until the time of Galileo, everyone accepted the Aristotelian concepts of physics. Aristotle taught that everything tries to seek its “proper place.” In Aristotle’s time it was thought that matter was made of four elements: air, fire, earth and water. Accordingly, he thought lighter objects fall mor ...
... Until the time of Galileo, everyone accepted the Aristotelian concepts of physics. Aristotle taught that everything tries to seek its “proper place.” In Aristotle’s time it was thought that matter was made of four elements: air, fire, earth and water. Accordingly, he thought lighter objects fall mor ...
Getting mathematical - Teaching Advanced Physics
... We need to get to a point where we can develop the equation F = - kx to a = -2x, where a is the acceleration and is the angular velocity associated with the SHM. To do this, we develop the graphical representation of SHM. Consider first the tethered trolley at its maximum displacement. Its veloci ...
... We need to get to a point where we can develop the equation F = - kx to a = -2x, where a is the acceleration and is the angular velocity associated with the SHM. To do this, we develop the graphical representation of SHM. Consider first the tethered trolley at its maximum displacement. Its veloci ...
S14 HPhys - cloudfront.net
... the velocities are the same. d. The more massive object will have less momentum if the velocities are the same. 25. The change in an object’s momentum is equal to a. the product of the mass of the object and the time interval. b. the product of the force applied to the object and the time interval. ...
... the velocities are the same. d. The more massive object will have less momentum if the velocities are the same. 25. The change in an object’s momentum is equal to a. the product of the mass of the object and the time interval. b. the product of the force applied to the object and the time interval. ...
Word version of Episode 302
... We need to get to a point where we can develop the equation F = - kx to a = -2x, where a is the acceleration and is the angular velocity associated with the SHM. To do this, we develop the graphical representation of SHM. Consider first the tethered trolley at its maximum displacement. Its veloci ...
... We need to get to a point where we can develop the equation F = - kx to a = -2x, where a is the acceleration and is the angular velocity associated with the SHM. To do this, we develop the graphical representation of SHM. Consider first the tethered trolley at its maximum displacement. Its veloci ...
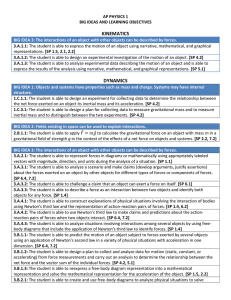
KINEMATICS DYNAMICS
... 2.B.1.1: The student is able to apply ⃗ ⃗ to calculate the gravitational force on an object with mass m in a gravitational field of strength g in the context of the effects of a net force on objects and systems. [SP 2.2, 7.2] BIG IDEA 3: The interactions of an object with other objects can be descri ...
... 2.B.1.1: The student is able to apply ⃗ ⃗ to calculate the gravitational force on an object with mass m in a gravitational field of strength g in the context of the effects of a net force on objects and systems. [SP 2.2, 7.2] BIG IDEA 3: The interactions of an object with other objects can be descri ...
Powerpoint
... General Force Model Newton 0th Law Objects are dumb - They have no memory of the past and cannot predict the future. Objects only know what is acting directly on them right now Newton's 1st Law An object that is at rest will remain at rest and an object that is moving will continue to move in a str ...
... General Force Model Newton 0th Law Objects are dumb - They have no memory of the past and cannot predict the future. Objects only know what is acting directly on them right now Newton's 1st Law An object that is at rest will remain at rest and an object that is moving will continue to move in a str ...
Nat 5 Physics Dynamics and space
... Calculating Distance Travelled from a Velocity-Time Graph If an object is accelerating it is often not possible to easily find its average speed. This in turn prevents the use of the equation distance = average speed x time to find the distance travelled. Thankfully there is another way we can use ...
... Calculating Distance Travelled from a Velocity-Time Graph If an object is accelerating it is often not possible to easily find its average speed. This in turn prevents the use of the equation distance = average speed x time to find the distance travelled. Thankfully there is another way we can use ...