notes5 Potential Energy Conservation
... This indicates that the potential energy change from position 1 to position 2 (i.e., the gain) ΔU=U2-U1 is equal to negative of the work done by the gravitational force W1-2 to move the mass from position 1 to position. For the mass to gain gravitational potential energy (i.e., ΔU=U2-U1>0), gravita ...
... This indicates that the potential energy change from position 1 to position 2 (i.e., the gain) ΔU=U2-U1 is equal to negative of the work done by the gravitational force W1-2 to move the mass from position 1 to position. For the mass to gain gravitational potential energy (i.e., ΔU=U2-U1>0), gravita ...
Chapter 6 Momentum and Impulse
... always true of kinetic energy. If the kinetic energy of the bodies involved in a collision is the same before and after impact, the collision is said to be a perfectly elastic collision. If the bodies stick together after impact, the collision is said to be completely inelastic. These represent the ...
... always true of kinetic energy. If the kinetic energy of the bodies involved in a collision is the same before and after impact, the collision is said to be a perfectly elastic collision. If the bodies stick together after impact, the collision is said to be completely inelastic. These represent the ...
Newton`s Laws - Petoskey Public Schools
... Newton’s three laws describe how things move and how this motion can be changed by other forces/objects Newton’s laws lead to the formulas that lets us express motion with math ...
... Newton’s three laws describe how things move and how this motion can be changed by other forces/objects Newton’s laws lead to the formulas that lets us express motion with math ...
Problem Set 6 - Cabrillo College
... divide by the denominator—the total mass will certainly be positive and will not affect the sign of the answer. So we could have done a simple mental calculation of the numerator (82 3 110 2) to figure out which football players ―wins.‖ P9.55: Most geologists believe that the dinosaurs became ...
... divide by the denominator—the total mass will certainly be positive and will not affect the sign of the answer. So we could have done a simple mental calculation of the numerator (82 3 110 2) to figure out which football players ―wins.‖ P9.55: Most geologists believe that the dinosaurs became ...
Dynamics - Bergen.org
... If you are told that mechanical energy is conserved, then you know it was a perfectly elastic collision. That allows you to use what we learned about conservation of energy in solving the problem. It turns out in this case that a very important general result can be obtained for perfectly elastic co ...
... If you are told that mechanical energy is conserved, then you know it was a perfectly elastic collision. That allows you to use what we learned about conservation of energy in solving the problem. It turns out in this case that a very important general result can be obtained for perfectly elastic co ...
Physics - Kalkaska Public Schools
... P3.1d Identify the basic forces in everyday interactions. P3.2A Identify the magnitude and direction of everyday forces (e.g., wind, tension in ropes, pushes and pulls, weight). P3.2B Compare work done in different situations. P3.2C Calculate the net force acting on an object. P3.2d Calculate all th ...
... P3.1d Identify the basic forces in everyday interactions. P3.2A Identify the magnitude and direction of everyday forces (e.g., wind, tension in ropes, pushes and pulls, weight). P3.2B Compare work done in different situations. P3.2C Calculate the net force acting on an object. P3.2d Calculate all th ...
Lab #5: The Work – Kinetic Energy Theorem
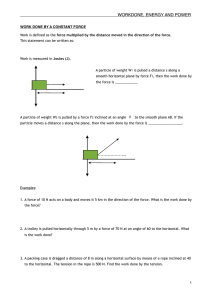
... subscript is “net”, for example, then the equation describes the Net (or Total) Work done on the object. It is important to clarify exactly which force, and therefore, work, is being described, because most objects are acted upon by more than one force simultaneously. The Total Work done on an obje ...
... subscript is “net”, for example, then the equation describes the Net (or Total) Work done on the object. It is important to clarify exactly which force, and therefore, work, is being described, because most objects are acted upon by more than one force simultaneously. The Total Work done on an obje ...
Ch 5 Work and Energy
... Heat is energy exchanged between objects because of a temperature difference. Heat originates in the internal energy of a substance. Internal energy is the sum of all the kinetic and potential energies associated with the molecules of the substance. For gases, internal energy is directly proportio ...
... Heat is energy exchanged between objects because of a temperature difference. Heat originates in the internal energy of a substance. Internal energy is the sum of all the kinetic and potential energies associated with the molecules of the substance. For gases, internal energy is directly proportio ...
Over head 2
... the card to accelerate horizontally. • Why did this happen? The force was applied to the card only – Inertia kept the coin from moving. • Do you think it would be different if you pulled it slowly? It should go with the card everytime. ...
... the card to accelerate horizontally. • Why did this happen? The force was applied to the card only – Inertia kept the coin from moving. • Do you think it would be different if you pulled it slowly? It should go with the card everytime. ...