normal force
... accelerates in the direction of the net force. The acceleration is directly proportional to the net force and inversely proportional to the object’s mass. The system has an ACCELERATION because the ...
... accelerates in the direction of the net force. The acceleration is directly proportional to the net force and inversely proportional to the object’s mass. The system has an ACCELERATION because the ...
Physics - Calderglen High School
... 7. A box slides down a smooth slope with an acceleration of 4 m s-2. The velocity of the box at a time t = 0 is 3 m s-1 down the slope. Using a = dv show by integration that the velocity, v, of the box is given by dt v = 3 + 4t. 8. The equation for the velocity, v, of a moving trolley is v = 2 + 6t. ...
... 7. A box slides down a smooth slope with an acceleration of 4 m s-2. The velocity of the box at a time t = 0 is 3 m s-1 down the slope. Using a = dv show by integration that the velocity, v, of the box is given by dt v = 3 + 4t. 8. The equation for the velocity, v, of a moving trolley is v = 2 + 6t. ...
Motion in one and two dimensions
... All motions are relative.The motion (velocity) of an object depends on which frame of reference is used to measure it. We say the measured velocity is relative to the chosen frame of reference. Usually the ground is the preferred choice as the reference frame and very often it is not specifically me ...
... All motions are relative.The motion (velocity) of an object depends on which frame of reference is used to measure it. We say the measured velocity is relative to the chosen frame of reference. Usually the ground is the preferred choice as the reference frame and very often it is not specifically me ...
F - Cloudfront.net
... Ex. #5: In a baseball game, the catcher stops a 90-mph pitch. What can you say about the work done by the catcher on the ball? 1) catcher has done positive work on the ball ...
... Ex. #5: In a baseball game, the catcher stops a 90-mph pitch. What can you say about the work done by the catcher on the ball? 1) catcher has done positive work on the ball ...
HNRS 227 Lecture #2 Chapters 2 and 3
... Questions for Thought An insect inside a bus flies from the back toward the front at 5.0 miles/hour. The bus is moving in a straight line at 50 miles/hour. What is the speed of the insect? The speed of the insect relative to the ground is the 50.0 mi/hr of the bus plus the 5.0 mi/hr of the insect ...
... Questions for Thought An insect inside a bus flies from the back toward the front at 5.0 miles/hour. The bus is moving in a straight line at 50 miles/hour. What is the speed of the insect? The speed of the insect relative to the ground is the 50.0 mi/hr of the bus plus the 5.0 mi/hr of the insect ...
Work, Power, and Energy
... Introduction • The explanations for the causes of motion described in this chapter do not rely on Newton's laws of motion but rather on the relationship between work, energy, and power • Some analyses and explanations are easier if based on work and energy relationships rather than Newtonian mechan ...
... Introduction • The explanations for the causes of motion described in this chapter do not rely on Newton's laws of motion but rather on the relationship between work, energy, and power • Some analyses and explanations are easier if based on work and energy relationships rather than Newtonian mechan ...
Chapter 6
... A change in momentum requires force and time. It requires more force to stop an object with a greater momentum than to stop an object with a smaller momentum. When Newton first expressed his second law, he wrote: F = ∆p ∆t force = change in momentum time interval ...
... A change in momentum requires force and time. It requires more force to stop an object with a greater momentum than to stop an object with a smaller momentum. When Newton first expressed his second law, he wrote: F = ∆p ∆t force = change in momentum time interval ...
MOMENTUM ! - Urbana School District #116
... Angular momentum depends on linear momentum and the distance from a particular point. It is a vector quantity with symbol L. If r and v are then the magnitude of angular momentum w/ resp. to point Q is given by L = rp = mvr. In this case L points out of the page. If the mass were moving in the opp ...
... Angular momentum depends on linear momentum and the distance from a particular point. It is a vector quantity with symbol L. If r and v are then the magnitude of angular momentum w/ resp. to point Q is given by L = rp = mvr. In this case L points out of the page. If the mass were moving in the opp ...
Chapter 8 Rotational Dynamics continued
... 1. Select the object to which the equations for equilibrium are to be applied. 2. Draw a free-body diagram that shows all of the external forces acting on the object. 3. Choose a convenient set of x, y axes and resolve all forces into components that lie along these axes. 4. Apply the equations t ...
... 1. Select the object to which the equations for equilibrium are to be applied. 2. Draw a free-body diagram that shows all of the external forces acting on the object. 3. Choose a convenient set of x, y axes and resolve all forces into components that lie along these axes. 4. Apply the equations t ...
MOMENTUM!
... Angular momentum depends on linear momentum and the distance from a particular point. It is a vector quantity with symbol L. If r and v are then the magnitude of angular momentum w/ resp. to point Q is given by L = r p = m v r. In this case L points out of the page. If the mass were moving in the op ...
... Angular momentum depends on linear momentum and the distance from a particular point. It is a vector quantity with symbol L. If r and v are then the magnitude of angular momentum w/ resp. to point Q is given by L = r p = m v r. In this case L points out of the page. If the mass were moving in the op ...
further questions
... 7. A box slides down a smooth slope with an acceleration of 4 m s-2. The velocity of the box at a time t = 0 is 3 m s-1 down the slope. Using a = dv show by integration that the velocity, v, of the box is given by dt v = 3 + 4t. 8. The equation for the velocity, v, of a moving trolley is v = 2 + 6t. ...
... 7. A box slides down a smooth slope with an acceleration of 4 m s-2. The velocity of the box at a time t = 0 is 3 m s-1 down the slope. Using a = dv show by integration that the velocity, v, of the box is given by dt v = 3 + 4t. 8. The equation for the velocity, v, of a moving trolley is v = 2 + 6t. ...
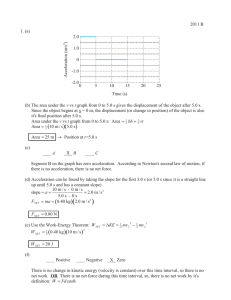
2011 B 1. (a) 2.0 0
... (b) Using the chalk, mark a starting line on the track. Using a tape metric measure or a meter stick, measure 10 m distances (marked by a chalk-line) up to, and including, 100 m (which is the finish line). Position one student, who has the starter's pistol, at the starting line. The ten other studen ...
... (b) Using the chalk, mark a starting line on the track. Using a tape metric measure or a meter stick, measure 10 m distances (marked by a chalk-line) up to, and including, 100 m (which is the finish line). Position one student, who has the starter's pistol, at the starting line. The ten other studen ...