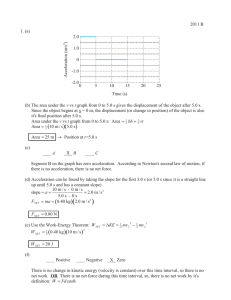
2011 B 1. (a) 2.0 0
... (b) Using the chalk, mark a starting line on the track. Using a tape metric measure or a meter stick, measure 10 m distances (marked by a chalk-line) up to, and including, 100 m (which is the finish line). Position one student, who has the starter's pistol, at the starting line. The ten other studen ...
... (b) Using the chalk, mark a starting line on the track. Using a tape metric measure or a meter stick, measure 10 m distances (marked by a chalk-line) up to, and including, 100 m (which is the finish line). Position one student, who has the starter's pistol, at the starting line. The ten other studen ...
Chapter 4 Forces and Newton’s Laws of Motion continued
... acceleration vector can be calculated. B) If the acceleration vector and mass of an object are known, then the Net Force acting on the object can be calculated. It may surprise you! C) If the acceleration vector and mass of an object are known, but the calculated Net Force and the identified forces ...
... acceleration vector can be calculated. B) If the acceleration vector and mass of an object are known, then the Net Force acting on the object can be calculated. It may surprise you! C) If the acceleration vector and mass of an object are known, but the calculated Net Force and the identified forces ...
Newton`s Laws
... Example – Angled Atwood’s Machine Masses m1 = 4.00 kg and m2 = 9.00 kg are connected by a light string that passes over a frictionless pulley. As shown in the diagram, m1 is held at rest on the floor and m2 rests on a fixed incline of angle 40 degrees. The masses are released from rest, and m2 slid ...
... Example – Angled Atwood’s Machine Masses m1 = 4.00 kg and m2 = 9.00 kg are connected by a light string that passes over a frictionless pulley. As shown in the diagram, m1 is held at rest on the floor and m2 rests on a fixed incline of angle 40 degrees. The masses are released from rest, and m2 slid ...
Full-text
... plate (5) gives 20% error. That’s because drag and lift coefficients are used. They show how much real force differs from calculated with (5). Some examples of drag coefficients for several basic shapes are shown below. So, it’s not important to use the “1/2”coefficient or not, but one must remember ...
... plate (5) gives 20% error. That’s because drag and lift coefficients are used. They show how much real force differs from calculated with (5). Some examples of drag coefficients for several basic shapes are shown below. So, it’s not important to use the “1/2”coefficient or not, but one must remember ...
Momentum and Impulse
... Change In Momentum The change in momentum is the difference in momentum from when the object is moving at its initial speed until it reaches its final speed. The unit of change in momentum is kg ms-1. ...
... Change In Momentum The change in momentum is the difference in momentum from when the object is moving at its initial speed until it reaches its final speed. The unit of change in momentum is kg ms-1. ...
The Nature of Force
... Mass is the amount of matter in an object. SI unit is the kilogram. The amount of inertia an object has depends on its mass. The greater the mass the greater the inertia. ...
... Mass is the amount of matter in an object. SI unit is the kilogram. The amount of inertia an object has depends on its mass. The greater the mass the greater the inertia. ...
What is energy?
... travels through space in the form of waves. Visible light and X-rays are examples. ...
... travels through space in the form of waves. Visible light and X-rays are examples. ...