Why did Einstein`s Programme supersede Lorentz`s? (II)
... disturbance propagates itself with velocity c independently of its source; the field may act back on the particles, thereby modifying their motion. Fields and particles are therefore ontologically on a par. One way of resolving this duaHsm is to explain the behaviour of the field in terms of the mec ...
... disturbance propagates itself with velocity c independently of its source; the field may act back on the particles, thereby modifying their motion. Fields and particles are therefore ontologically on a par. One way of resolving this duaHsm is to explain the behaviour of the field in terms of the mec ...
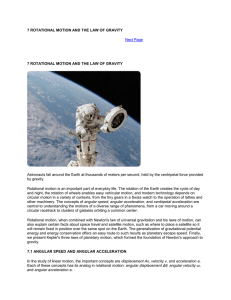
Chapter 8 Accelerated Circular Motion
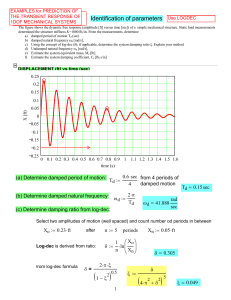
... 1. Make a drawing. 2. Decide which directions are to be called positive (+) and negative (–). 3. Write down the values that are given for any of the five kinematic variables. 4. Verify that the information contains values for at least three of the five kinematic variables. Select the appropriate equ ...
... 1. Make a drawing. 2. Decide which directions are to be called positive (+) and negative (–). 3. Write down the values that are given for any of the five kinematic variables. 4. Verify that the information contains values for at least three of the five kinematic variables. Select the appropriate equ ...
Table of Contents
... In order to have forces cancel out; they have to be different forces. An example of this would be if we had two horses hitched to the same wagon pulling in opposite directions. The forces the horses exert would then cancel out and the wagon wouldn’t move. These would be two separate forces that do c ...
... In order to have forces cancel out; they have to be different forces. An example of this would be if we had two horses hitched to the same wagon pulling in opposite directions. The forces the horses exert would then cancel out and the wagon wouldn’t move. These would be two separate forces that do c ...
CHAPTER 9 ROTATIONAL DYNAMICS
... the forces, as well as the vector sum of all the torques, that act on the system must be zero. The figure below shows a free body diagram for the boom. Since the boom is assumed to be uniform, its weight W B is located at its center of gravity, which coincides with its geometrical center. There is a ...
... the forces, as well as the vector sum of all the torques, that act on the system must be zero. The figure below shows a free body diagram for the boom. Since the boom is assumed to be uniform, its weight W B is located at its center of gravity, which coincides with its geometrical center. There is a ...
chapter 1 introduction and basic concepts
... Pound-mass lbm is the mass unit in English system whereas pound-force lbf is the force unit in the English system. One pound-force is the force required to accelerate a mass of 32.174 lbm by 1 ft/s2. In other words, the weight of a 1-lbm mass at sea level on earth is 1 lbf. Discussion ...
... Pound-mass lbm is the mass unit in English system whereas pound-force lbf is the force unit in the English system. One pound-force is the force required to accelerate a mass of 32.174 lbm by 1 ft/s2. In other words, the weight of a 1-lbm mass at sea level on earth is 1 lbf. Discussion ...