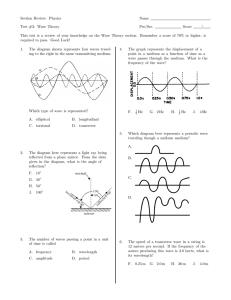
Chapter – 12 Simple Harmonic Motion
... Q 13. A spring stores 5J of energy when stretched by 25 cm. It is kept vertical with the lower end fixed. A block fastened to its other end is made to undergo small oscillations. If the block makes 5 oscillations each second, what is the mass of the block ? Q 14. A small block of mass m is kept on a ...
... Q 13. A spring stores 5J of energy when stretched by 25 cm. It is kept vertical with the lower end fixed. A block fastened to its other end is made to undergo small oscillations. If the block makes 5 oscillations each second, what is the mass of the block ? Q 14. A small block of mass m is kept on a ...
forces - U of M Physics
... spring-object system in a consistent manner. Decide how many measurements you will need to make a reliable determination of the spring constant. Method #2: Secure one end of the spring safely to the metal rod and select a mass that gives a regular oscillation without excessive wobbling to the hangin ...
... spring-object system in a consistent manner. Decide how many measurements you will need to make a reliable determination of the spring constant. Method #2: Secure one end of the spring safely to the metal rod and select a mass that gives a regular oscillation without excessive wobbling to the hangin ...
CONTENTS - teko classes bhopal
... To locate the position of object we need a frame of reference. A convenient way to set up a frame of reference is to choose three mutually perpendicular axis and name them x-y-z axis. The coordinates (x, y, z) of the particle then specify the position of object w.r.t. that frame. If any one o more c ...
... To locate the position of object we need a frame of reference. A convenient way to set up a frame of reference is to choose three mutually perpendicular axis and name them x-y-z axis. The coordinates (x, y, z) of the particle then specify the position of object w.r.t. that frame. If any one o more c ...
ENERGY AND WORK
... process is lost when the object is brought the rest. Assess: Kinetic energy does not change if an object has the same velocity at the beginning and end of a process. ...
... process is lost when the object is brought the rest. Assess: Kinetic energy does not change if an object has the same velocity at the beginning and end of a process. ...
Physics 207: Lecture 2 Notes
... Consider the following two cases (a falling ball and ball on table), Compare and contrast Free Body Diagram and Action-Reaction Force Pair sketch ...
... Consider the following two cases (a falling ball and ball on table), Compare and contrast Free Body Diagram and Action-Reaction Force Pair sketch ...
Grade 9 Physics - Hammonton Public Schools
... principles, including fundamental ideas about matter, energy, and motion, are powerful conceptual tools for making sense of phenomena in physical, living, and Earth systems science. E. Forces and Motion : It takes energy to change the motion of objects. The energy change is understood in terms of fo ...
... principles, including fundamental ideas about matter, energy, and motion, are powerful conceptual tools for making sense of phenomena in physical, living, and Earth systems science. E. Forces and Motion : It takes energy to change the motion of objects. The energy change is understood in terms of fo ...
TEST-Chapters 2-4-Clayton Answer Section
... ____ 14. According to Newton's second law of motion, ____. a. F = m a c. F = p a b. F = m v d. F = p v ____ 15. For any object, the greater the force that's applied to it, the greater its ____ will be. a. acceleration c. inertia b. gravity d. velocity ____ 16. When a force is exerted on a bo ...
... ____ 14. According to Newton's second law of motion, ____. a. F = m a c. F = p a b. F = m v d. F = p v ____ 15. For any object, the greater the force that's applied to it, the greater its ____ will be. a. acceleration c. inertia b. gravity d. velocity ____ 16. When a force is exerted on a bo ...
Rotational Motion
... For a table of corresponding relationships Translational:Rotational see table 10.3 on page 261 Herriman High AP Physics C ...
... For a table of corresponding relationships Translational:Rotational see table 10.3 on page 261 Herriman High AP Physics C ...
canim-11 - The University of Texas at Dallas
... • In practice, our simple implementation of the particle system will guarantee conservation of momentum, due to the way we formulated it • It will not, however guarantee the conservation of energy, and in practice, we might see a gradual increase or decrease in system energy over time • A gradual de ...
... • In practice, our simple implementation of the particle system will guarantee conservation of momentum, due to the way we formulated it • It will not, however guarantee the conservation of energy, and in practice, we might see a gradual increase or decrease in system energy over time • A gradual de ...
8.5 Collisions 8 Momentum
... 8.4 Conservation of Momentum The force or impulse that changes momentum must be exerted on the object by something outside the object. • Molecular forces within a basketball have no effect on the momentum of the basketball. • A push against the dashboard from inside does not affect the momentum of a ...
... 8.4 Conservation of Momentum The force or impulse that changes momentum must be exerted on the object by something outside the object. • Molecular forces within a basketball have no effect on the momentum of the basketball. • A push against the dashboard from inside does not affect the momentum of a ...
Devil physics The baddest class on campus IB Physics
... introduction to the topic reminds us that not all oscillations are isochronous. However, the simple harmonic oscillator is of great importance to physicists because all periodic oscillations can be described through the mathematics of simple harmonic motion. ...
... introduction to the topic reminds us that not all oscillations are isochronous. However, the simple harmonic oscillator is of great importance to physicists because all periodic oscillations can be described through the mathematics of simple harmonic motion. ...
Newton`s Laws
... 1.) There are two ways to deal with Newton's Second Law problems. a.) The first is the formal, technically kosher way to proceed. It has specific steps and works on even the most convoluted force/acceleration problems. These include situations in which forces do not act in the same direction as the ...
... 1.) There are two ways to deal with Newton's Second Law problems. a.) The first is the formal, technically kosher way to proceed. It has specific steps and works on even the most convoluted force/acceleration problems. These include situations in which forces do not act in the same direction as the ...
laws of motion - WordPress.com
... A 200-N wagon is to be pulled up a 308 incline at constant speed. How large a force parallel to the incline is needed if friction eects are negligible? The situation is shown in Fig. 3-10(a). Because the wagon moves at a constant speed along a straight line, its velocity vector is constant. Therefo ...
... A 200-N wagon is to be pulled up a 308 incline at constant speed. How large a force parallel to the incline is needed if friction eects are negligible? The situation is shown in Fig. 3-10(a). Because the wagon moves at a constant speed along a straight line, its velocity vector is constant. Therefo ...
Friction Intro - HRSBSTAFF Home Page
... Rough surface means more friction (ie, larger coefficient of friction) Magnitude of forces pressing surfaces together (mass) More mass means more friction ...
... Rough surface means more friction (ie, larger coefficient of friction) Magnitude of forces pressing surfaces together (mass) More mass means more friction ...