Document
... A solid cylinder and a hoop roll down an incline. Both are the same mass and radius. Which reaches the bottom of the incline first? 1. The cylinder 2. The hoop 3. Both at same time "An object's moment of inertia determines how much it resists rotational motion. The cylinder has a smaller moment of ...
... A solid cylinder and a hoop roll down an incline. Both are the same mass and radius. Which reaches the bottom of the incline first? 1. The cylinder 2. The hoop 3. Both at same time "An object's moment of inertia determines how much it resists rotational motion. The cylinder has a smaller moment of ...
Lab Writeup Moment of Inertia
... If we apply a single, unbalanced force, F, to an object, the object will undergo linear acceleration, a, which is determined by the force and the mass, m, of the object. The mass is a measure of the object’s resistance to changing velocity, its inertia. This relationship is written F ma . If we ...
... If we apply a single, unbalanced force, F, to an object, the object will undergo linear acceleration, a, which is determined by the force and the mass, m, of the object. The mass is a measure of the object’s resistance to changing velocity, its inertia. This relationship is written F ma . If we ...
+ Rotational motion about its CM
... and two identical bullets hit into it symmetrically. The angular velocity of system will ________ A. increase; B. decrease; C. remain constant Solution: Total angular momentum of the system is conserved ...
... and two identical bullets hit into it symmetrically. The angular velocity of system will ________ A. increase; B. decrease; C. remain constant Solution: Total angular momentum of the system is conserved ...
Unit 1 - Edexcel
... because it could be beaten to make large flat objects, such as shields, as well as being drawn into wires which could be used decoratively. Name and define the property of copper that makes it suitable for this method of making shields and the property that makes it suitable for making wires. ...
... because it could be beaten to make large flat objects, such as shields, as well as being drawn into wires which could be used decoratively. Name and define the property of copper that makes it suitable for this method of making shields and the property that makes it suitable for making wires. ...
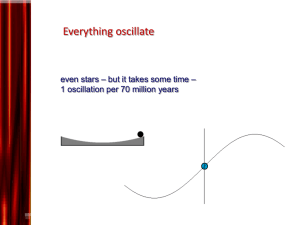
Oscillations (PPT) - Uplift North Hills Prep
... fix a “damper” to the springs. If placed on the strings in the correct position, this has the effect of producing critically damped oscillations and as a result the struck tennis racquet moves smoothly back to equilibrium. In addition, vibrations caused by the impact of the ball with the strings of ...
... fix a “damper” to the springs. If placed on the strings in the correct position, this has the effect of producing critically damped oscillations and as a result the struck tennis racquet moves smoothly back to equilibrium. In addition, vibrations caused by the impact of the ball with the strings of ...
Newton’s Laws of Motion - U
... • The tendency of an object’s motion to remain constant, or , put another way… • The tendency of an object to resist a change in it’s motion (either speed or direction) • We may measure inertia as mass (kg) • Can you think of some low inertia objects??? • Some very high inertia objects? ...
... • The tendency of an object’s motion to remain constant, or , put another way… • The tendency of an object to resist a change in it’s motion (either speed or direction) • We may measure inertia as mass (kg) • Can you think of some low inertia objects??? • Some very high inertia objects? ...
SPH3U Exam Solutions Lisa Di Lorenzo - ped4126-2010
... addressing the expectations of B2.7 to solve problems involving uniform linear motion in two dimensions. From B2.6, it is evident that students have some knowledge of vector diagrams and components and using them to solve problems in uniform acceleration equations. I allotted half a mark for the ini ...
... addressing the expectations of B2.7 to solve problems involving uniform linear motion in two dimensions. From B2.6, it is evident that students have some knowledge of vector diagrams and components and using them to solve problems in uniform acceleration equations. I allotted half a mark for the ini ...