Wk9Dy1 - Elimination StudentHandout SofEq
... equation is introduced to form a system of two linear equations. When asked to graph x + 2y = 8 and 4x – y = 5, a student in Mrs. Reed’s class produced the results found in page 3.1 Note: to graph these equations this student first solved each equation for y so that they could be graphed as function ...
... equation is introduced to form a system of two linear equations. When asked to graph x + 2y = 8 and 4x – y = 5, a student in Mrs. Reed’s class produced the results found in page 3.1 Note: to graph these equations this student first solved each equation for y so that they could be graphed as function ...
Worked solution of problem similar to M1 3X – 5y = 13 4X + 8y = 7
... So 44y = -31 (Then divide both sides of the equation by 44) So y =-31/44 = 0.704545 (exactly or 0.70 if the answer is to an engineering question that might only requires accuracy of about +/- 1%. In this case none of the numbers in the problem are expressed to more than 2 significant figures so it i ...
... So 44y = -31 (Then divide both sides of the equation by 44) So y =-31/44 = 0.704545 (exactly or 0.70 if the answer is to an engineering question that might only requires accuracy of about +/- 1%. In this case none of the numbers in the problem are expressed to more than 2 significant figures so it i ...
MM405A : Differential Equations
... Uniqueness of solutions, Lipschitz condition, Picard-Lindelof existence and uniqueness theorem for ...
... Uniqueness of solutions, Lipschitz condition, Picard-Lindelof existence and uniqueness theorem for ...
File
... We can think of equations as input-output machines. The x-values being the “inputs” and the y-values being the “outputs.” Choosing any value for input and plugging it into the equation, we solve for the output. ...
... We can think of equations as input-output machines. The x-values being the “inputs” and the y-values being the “outputs.” Choosing any value for input and plugging it into the equation, we solve for the output. ...
How to Graph a Line – Chapter 3
... A. Multiply one (or both) equation by some number which will make the coefficient of one of the variables the SAME NUMBER WITH DIFFERENT SIGNS (hint, look for different signs in front of the variable, otherwise you will need to multiply by a negative number) B. Add the equations to eliminate one of ...
... A. Multiply one (or both) equation by some number which will make the coefficient of one of the variables the SAME NUMBER WITH DIFFERENT SIGNS (hint, look for different signs in front of the variable, otherwise you will need to multiply by a negative number) B. Add the equations to eliminate one of ...
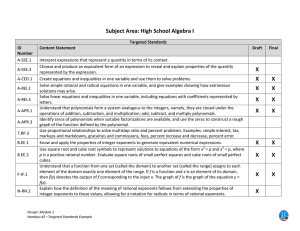
August 22, 2008 page 1 Self-Assessment: Algebra 1 On a scale of 5
... A1.7.A Sketch the graph for an exponential function of the form y = abn where n is an integer, describe the effects that changes in the parameters a and b have on the graph, and answer questions that arise in situations modeled by exponential functions. A1.7.B Find and approximate solutions to expon ...
... A1.7.A Sketch the graph for an exponential function of the form y = abn where n is an integer, describe the effects that changes in the parameters a and b have on the graph, and answer questions that arise in situations modeled by exponential functions. A1.7.B Find and approximate solutions to expon ...
3.6 - Bryan City Schools
... Systems of three equations with three variables are often called 3-by-3 systems. In general, to find a single solution to any system of equations, you need as many equations as you have variables. Recall from Lesson 3-5 that the graph of a linear equation in three variables is a plane. When you grap ...
... Systems of three equations with three variables are often called 3-by-3 systems. In general, to find a single solution to any system of equations, you need as many equations as you have variables. Recall from Lesson 3-5 that the graph of a linear equation in three variables is a plane. When you grap ...