Download 3.6 - Bryan City Schools

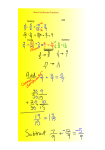
Systems of three equations with three variables are often called
3-by-3 systems. In general, to find a single solution to any
system of equations, you need as many equations as you have
variables.
Recall from Lesson 3-5
that the graph of a linear
equation in three variables
is a plane. When you
graph a system of three
linear equations in three
dimensions, the result is
three planes that may or
may not intersect. The
solution to the system is
the set of points where all
three planes intersect.
These systems may have
one, infinitely many, or no
solution.
Identifying the exact solution from a graph of a 3-by-3 system can
be very difficult. However, you can use the methods of elimination
and substitution to reduce a 3-by-3 system to a 2-by-2 system and
then use the methods that you learned in Lesson 3-2.
Ex 1: Use elimination to solve the system of equations.
5x – 2y – 3z = –7
1
2x – 3y + z = –16
2
3x + 4y – 2z = 7
3
Step 1 Eliminate one variable.
In this system, z is a reasonable choice to eliminate first
because the coefficient of z in the second equation is 1 and z is
easy to eliminate from the other equations.
1
2
5x – 2y – 3z = –7
3(2x –3y + z = –16)
Use equations
in x and y.
3
5x – 2y – 3z = –7 Multiply equation
-2 by 3, and add
6x – 9y + 3z = –48 to equation 1 .
11x – 11y
= –55 4
and 2 to create a second equation
1
3
2
Multiply equation
-2 by 2, and add
to equation 3 .
3x + 4y – 2z = 7
3x + 4y – 2z = 7
2(2x –3y + z = –16) 4x – 6y + 2z = –32
7x – 2y
= –25
5
You now have a 2-by-2 system.
11x – 11y = –55
7x – 2y = –25
4
5
Step 2 Eliminate another variable. Then solve for the remaining
variable.
You can eliminate y by using methods from Lesson 3-2.
4
5
–2(11x – 11y = –55)
11(7x – 2y = –25)
–22x + 22y = 110
77x – 22y = –275
55x
Multiply equation
-4 by –2, and
equation -5 by 11
1 and add.
= –165
x =1–3
Step 3 Use one of the equations in your 2-by-2 system to solve for
y.
4
11x – 11y = –55
11(–3) – 11y = –55
y=2
Step 4 Substitute for x and y in one of the original equations to
solve for z.
2
2x – 3y + z = –16
2(–3) – 3(2) + z = –16
z = –4
1
The solution is (–3, 2, –4).
1
You can also use substitution to solve a 3-by-3 system. Again, the
first step is to reduce the 3-by-3 system to a 2-by-2 system.
Ex 2: The table shows the number of each type of ticket sold and
the total sales amount for each night of the school play.
Find the price of each type of ticket.
Orchestra
Mezzanine
Balcony
Total Sales
Fri
200
30
40
$1470
Sat
250
60
50
$1950
Sun
150
30
0
$1050
Step 1 Let x represent the price of an orchestra seat, y represent
the price of a mezzanine seat, and z represent the present of a
balcony seat.
Write a system of equations to represent the data in the table.
200x + 30y + 40z = 1470
1
250x + 60y + 50z = 1950
2
Saturday’s sales.
150x + 30y = 1050
3
Sunday’s sales.
Friday’s sales.
A variable is “missing” in the last equation; however, the same solution
methods apply. Elimination is a good choice because eliminating z is
straightforward.
Step 2 Eliminate z.
Multiply equation 1 by 5 and equation 2 by –4 and add.
1
5(200x + 30y + 40z = 1470)
2
–4(250x + 60y + 50z = 1950)
1000x + 150y + 200z = 7350
–1000x – 240y – 200z = –7800
y
=5
1
By eliminating z, due to the coefficients of x, you also eliminated x
providing a solution for y.
Step 3 Use equation
to solve for x.
3
150x + 30y = 1050
150x + 30(5) = 1050
x=6
3
Step 4 Use equations
to solve for z.
1
1
or
2
200x + 30y + 40z = 1470
200(6) + 30(5) + 40z = 1470
z=3
The solution to the system is (6, 5, 3). So, the cost of an orchestra seat is
$6, the cost of a mezzanine seat is $5, and the cost of a balcony seat is $3.
Ex 3: Classify the system as consistent or inconsistent, and
determine the number of solutions.
2x – 6y + 4z = 2
–3x + 9y – 6z = –3
5x – 15y + 10z = 5
1
2
3
The elimination method is convenient because the numbers you
need to multiply the equations are small.
First, eliminate x.
Multiply equation
1
by 3 and equation 2 by 2 and add.
1
3(2x – 6y + 4z = 2)
6x – 18y + 12z = 6
2
2(–3x + 9y – 6z = –3)
–6x + 18y – 12z = –6
0=0

1
3
Multiply equation 1 by 5 and equation 3 by –2
and add.
10x – 30y + 20z = 10
5(2x – 6y + 4z = 2)
–10x + 30y – 20z = –10
–2(5x – 15y + 10z = 5)
0 = 0 
Because 0 is always equal to 0, the equation is
an identity. Therefore, the system is consistent,
dependent and has an infinite number of solutions.