Download How to Graph a Line – Chapter 3

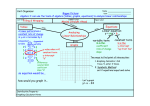
How to Graph a Line
I. Always label the x and y axis
II. Method for graphing linear equations ax+by=c – Do A or B
A. Substitution Chart (x-y table)
1. Substitute ANY value of one of the variables in the chart. Solve for the other
variable using that value
a. OPTIONAL: Substitute x=0 to get the y-intercept (point is (0,y))
b. OPTIONAL: Substitute y=0 to get the x-intercept (point is (x,0))
2. Create at least 3 points (2 are necessary, 1 is a check)
3. Plot these points on the graph
B. Slope, y-intercept method (y=mx+b form)
1. Solve the equation for y [THIS IS THE HARD PART]
2. Plot b on the y-axis [this is the y-intercept because if you let x=0, you get y=b AND
the point is (0,b)]
3. Use the fraction form of slope (m is the coefficient of x) to move up/down and
left/right to create more points for your line – SLOPE = RISE/RUN
III. Make a line through the points and beyond
IV. Put arrows at the end of this line to show infinity
V. Write the original equation on the line to label it
Other Useful Facts about Lines - Intercepts
I. To find the x-intercept, set y=0
II. To find the x-intercept, set y=0
Other Useful Facts about Lines - Slopes
I. Finding the slope when given two (x,y) coordinates.
Substitute the coordinate values in the formula: m 
y1  y2
x1  x2
II. Y = # is a Horizontal line.
Slope of a HORIZONTAL line is ZERO;
III. X = # is a Vertical line.
Slope of a VERTICAL line is UNDEFINED
Solving a System of (Two Linear) Equations
Nice Solutions:
 Intersecting Lines have ONE SOLUTION
o The 2 lines have different slopes
o The Solution (x,y) must check in
BOTH equations
o Perpendicular lines have slopes
that are negative reciprocals
Naughty Solutions:
 Parallel Lines have NO SOLUTIONS
o INCONSISTENT
o Same Slope
o Different y-intercept
o Results in FALSE statements
 Same Lines have INFINITE SOLUTIONS
o DEPENDENT
o All points are equal on both lines
o Same Slope
o Same y-intercept
o Results in TRUE statements
Solving a System of Equations
I. Solve by Graphing
A. Graph Equation A (this is a line – see chapter 3 notes above)
B. Graph Equation B on the same axis (this is a line too)
C. Read the intersection point (x,y)
D. Check it in equation A AND equation B
II. Solve by Elimination
A. Multiply one (or both) equation by some number which will make the coefficient of one of
the variables the SAME NUMBER WITH DIFFERENT SIGNS (hint, look for different
signs in front of the variable, otherwise you will need to multiply by a negative number)
B. Add the equations to eliminate one of the variable and get an equation in one variable
C. Solve for this variable
D. Go back to either equation to find the value of the other variable by substituting what you
got in step C. The solution is (x,y)
E. Check x and y values in both equations
III. Solve by Substitution
A. Solve one equation for either variable (hint, look for a coefficient of 1, otherwise you will have
to divide and may end up with fractions)
B. Substitute that expression into the OTHER EQUATION to make an equation which has one
variable
C. Solve for this variable
D. Go back to either equation to find the value of the other variable by substituting what you got
in step C. The solution is (x,y)
E. Check x and y values in both equations