Logistic Regression - Virgil Zeigler-Hill
... than two categories It (basically) works in the same way as binary logistic regression The analysis breaks the outcome variable down into a series of comparisons between two categories. – Example: if you have three outcome categories (A, B, and C), ...
... than two categories It (basically) works in the same way as binary logistic regression The analysis breaks the outcome variable down into a series of comparisons between two categories. – Example: if you have three outcome categories (A, B, and C), ...
chapter14
... Many researchers have examined factors that are believed to contribute to the risk of heart attacks. One study found that hip-to-waist ratio was a better predictor of heart attacks than body-mass index. A plot of data from this study of a measure heart-attack risk (y) versus hip-to-waist ratio (x) ...
... Many researchers have examined factors that are believed to contribute to the risk of heart attacks. One study found that hip-to-waist ratio was a better predictor of heart attacks than body-mass index. A plot of data from this study of a measure heart-attack risk (y) versus hip-to-waist ratio (x) ...
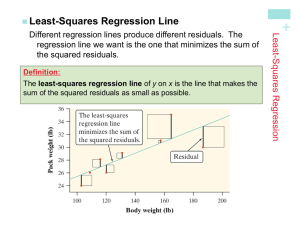
Correlation and Simple Linear Regression
... Correlation and Simple Linear Regression We are often interested in studying the relationship among variables to determine whether they are associated with one another. When we think that changes in a variable x explain, or maybe even cause, changes in a second variable y, we call x an explanatory v ...
... Correlation and Simple Linear Regression We are often interested in studying the relationship among variables to determine whether they are associated with one another. When we think that changes in a variable x explain, or maybe even cause, changes in a second variable y, we call x an explanatory v ...
Exploration A
... Exploration 13A: Revenue and Demand Functions File “C13 Exploration A.xls” contains weekly sales and revenue information for two different companies. The first worksheet, labeled “Company 1” shows the quantities of two complementary commodities that are sold by this company. These items are X and Y. ...
... Exploration 13A: Revenue and Demand Functions File “C13 Exploration A.xls” contains weekly sales and revenue information for two different companies. The first worksheet, labeled “Company 1” shows the quantities of two complementary commodities that are sold by this company. These items are X and Y. ...
Logistic regression models were developed to examine the
... Consensus guidelines and expert opinion were followed to implement propensity score matching with the greatest validity and precision. Logistic regression modelling was used to generate the probability of EMS interval within 60 minutes. A non-parsimonious modelling strategy was utilised including al ...
... Consensus guidelines and expert opinion were followed to implement propensity score matching with the greatest validity and precision. Logistic regression modelling was used to generate the probability of EMS interval within 60 minutes. A non-parsimonious modelling strategy was utilised including al ...
Regression Basics
... • How close are our estimates to the true population values of the slope and intercept? • We can never know for sure, but we can construct a range of values such that we are confident, at some definite level of probability, that the true value will fall within this range. • This is called a “confide ...
... • How close are our estimates to the true population values of the slope and intercept? • We can never know for sure, but we can construct a range of values such that we are confident, at some definite level of probability, that the true value will fall within this range. • This is called a “confide ...
Document
... The Division of Engineering is offering a part-time teaching position in Summer 2017 and is looking for candidates with a minimum of a Master’s degree, with a PhD or industrial experience preferred. EGNE 2309 - Probability and Statistics for Engineers Class period: July 5 – August 23, 2017 Lecture: ...
... The Division of Engineering is offering a part-time teaching position in Summer 2017 and is looking for candidates with a minimum of a Master’s degree, with a PhD or industrial experience preferred. EGNE 2309 - Probability and Statistics for Engineers Class period: July 5 – August 23, 2017 Lecture: ...
Linear regression
In statistics, linear regression is an approach for modeling the relationship between a scalar dependent variable y and one or more explanatory variables (or independent variables) denoted X. The case of one explanatory variable is called simple linear regression. For more than one explanatory variable, the process is called multiple linear regression. (This term should be distinguished from multivariate linear regression, where multiple correlated dependent variables are predicted, rather than a single scalar variable.)In linear regression, data are modeled using linear predictor functions, and unknown model parameters are estimated from the data. Such models are called linear models. Most commonly, linear regression refers to a model in which the conditional mean of y given the value of X is an affine function of X. Less commonly, linear regression could refer to a model in which the median, or some other quantile of the conditional distribution of y given X is expressed as a linear function of X. Like all forms of regression analysis, linear regression focuses on the conditional probability distribution of y given X, rather than on the joint probability distribution of y and X, which is the domain of multivariate analysis.Linear regression was the first type of regression analysis to be studied rigorously, and to be used extensively in practical applications. This is because models which depend linearly on their unknown parameters are easier to fit than models which are non-linearly related to their parameters and because the statistical properties of the resulting estimators are easier to determine.Linear regression has many practical uses. Most applications fall into one of the following two broad categories: If the goal is prediction, or forecasting, or error reduction, linear regression can be used to fit a predictive model to an observed data set of y and X values. After developing such a model, if an additional value of X is then given without its accompanying value of y, the fitted model can be used to make a prediction of the value of y. Given a variable y and a number of variables X1, ..., Xp that may be related to y, linear regression analysis can be applied to quantify the strength of the relationship between y and the Xj, to assess which Xj may have no relationship with y at all, and to identify which subsets of the Xj contain redundant information about y.Linear regression models are often fitted using the least squares approach, but they may also be fitted in other ways, such as by minimizing the ""lack of fit"" in some other norm (as with least absolute deviations regression), or by minimizing a penalized version of the least squares loss function as in ridge regression (L2-norm penalty) and lasso (L1-norm penalty). Conversely, the least squares approach can be used to fit models that are not linear models. Thus, although the terms ""least squares"" and ""linear model"" are closely linked, they are not synonymous.