lecture31
... numbers also result in small energy differences • Pauli exclusion principle: no two electrons in the same atom can be in the same quantum state • Electrons are grouped into shells and subshells • Periodic table reflects shell structure •Atoms with the same number of electrons in their outer shells h ...
... numbers also result in small energy differences • Pauli exclusion principle: no two electrons in the same atom can be in the same quantum state • Electrons are grouped into shells and subshells • Periodic table reflects shell structure •Atoms with the same number of electrons in their outer shells h ...
lecture31
... There are four different quantum numbers needed to specify the state of an electron in an atom: 1) Principal quantum number n gives the total energy: ...
... There are four different quantum numbers needed to specify the state of an electron in an atom: 1) Principal quantum number n gives the total energy: ...
Electrons!
... The first quantum number, the principal quantum number, n, can have positive integral values of 1, 2, 3, etc. As n increases, the orbital becomes larger and the electron is farther from the nucleus. An increase in n also means that the electron has a higher energy and is less tightly bound to th ...
... The first quantum number, the principal quantum number, n, can have positive integral values of 1, 2, 3, etc. As n increases, the orbital becomes larger and the electron is farther from the nucleus. An increase in n also means that the electron has a higher energy and is less tightly bound to th ...
Solid State Physics
... Consider two different atoms, such as Ga and As joined by a covalent bond. The functions come from different orbitals. The C constants would be different. The wave function still spreads between the atoms, but the probability is that the shared electron will be nearer to one atom than another. Ato ...
... Consider two different atoms, such as Ga and As joined by a covalent bond. The functions come from different orbitals. The C constants would be different. The wave function still spreads between the atoms, but the probability is that the shared electron will be nearer to one atom than another. Ato ...
Chapter 7, 8, and 9 Exam 2014 Name I. 50% of your grade will come
... Chapter 7, 8, and 9 Exam 2016 ...
... Chapter 7, 8, and 9 Exam 2016 ...
Double-Slit Experiment
... Curved (accelerated) motion means that electron should do what? = ASSUMPTIONS BASED IN CLASSICAL PHYSICS!!! Quantum physics: ...
... Curved (accelerated) motion means that electron should do what? = ASSUMPTIONS BASED IN CLASSICAL PHYSICS!!! Quantum physics: ...
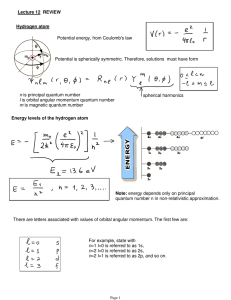
Lecture 12: Review.
... 1. Make sure that you know, understand and can use all formulas and concepts from this lecture and previous lecture notes. 2. Make sure that you can solve on your own and without looking into any notes any problem done in class in Lectures or from homeworks (if integrals are complicated, use Maple, ...
... 1. Make sure that you know, understand and can use all formulas and concepts from this lecture and previous lecture notes. 2. Make sure that you can solve on your own and without looking into any notes any problem done in class in Lectures or from homeworks (if integrals are complicated, use Maple, ...
Chemistry Electrons in Atoms Outline
... 1. we cannot tell the position and the momentum of an electron simultaneously (at the same time) 2. by observing an electron with light we actually change the electron’s position or its momentum C. Schrodinger Wave Equation 1. this equation describes mathematically the wave properties of electrons a ...
... 1. we cannot tell the position and the momentum of an electron simultaneously (at the same time) 2. by observing an electron with light we actually change the electron’s position or its momentum C. Schrodinger Wave Equation 1. this equation describes mathematically the wave properties of electrons a ...
4.2_The_Quantum_Model_of_the_Atom1
... The Schrödinger Wave Equation • In 1926, Austrian physicist Erwin Schrödinger developed an equation that treated electrons in atoms as waves. • Together with the Heisenberg uncertainty principle, the Schrödinger wave equation laid the foundation for modern quantum theory. • Quantum theory describes ...
... The Schrödinger Wave Equation • In 1926, Austrian physicist Erwin Schrödinger developed an equation that treated electrons in atoms as waves. • Together with the Heisenberg uncertainty principle, the Schrödinger wave equation laid the foundation for modern quantum theory. • Quantum theory describes ...
LOYOLA COLLEGE (AUTONOMOUS), CHENNAI – 600 034
... b. If the bond length of C-C is 1.48 Ǻ and C=C is 1.34 Ǻ, calculate the penetration effect. ...
... b. If the bond length of C-C is 1.48 Ǻ and C=C is 1.34 Ǻ, calculate the penetration effect. ...
Document
... • An electron is characterized by quantum numbers. These can be measured without uncertainty. • The quantum number n labels the energy level En . • The lowest energy level with n = 1 is sharp (E= 0), because an atom is stable. One can take an infinite time (t = ) to determine its energy and there ...
... • An electron is characterized by quantum numbers. These can be measured without uncertainty. • The quantum number n labels the energy level En . • The lowest energy level with n = 1 is sharp (E= 0), because an atom is stable. One can take an infinite time (t = ) to determine its energy and there ...
unit 7 hw packet File
... A. Analyze the relationship between energy, frequency, and wavelength of light (both qualitatively and quantitatively). B. Compare and contrast different regions of the electromagnetic spectrum. C. Distinguish between ground state and excited state electrons. D. Explain how spectral lines can be use ...
... A. Analyze the relationship between energy, frequency, and wavelength of light (both qualitatively and quantitatively). B. Compare and contrast different regions of the electromagnetic spectrum. C. Distinguish between ground state and excited state electrons. D. Explain how spectral lines can be use ...
Electrons in Atoms
... quantized energy levels. Unlike Bohr, the quantum mechanical model does not define an exact pathway for electrons. • The quantum mechanical model is concerned with the probability of finding an electron. • At this point, electrons can be explained in terms of waves, particles and beyond. ...
... quantized energy levels. Unlike Bohr, the quantum mechanical model does not define an exact pathway for electrons. • The quantum mechanical model is concerned with the probability of finding an electron. • At this point, electrons can be explained in terms of waves, particles and beyond. ...
Fall 2011 CHEM 760: Introductory Quantum Chemistry Homework 9
... Lˆ z ,total Lˆ z1 Lˆ z 2 and S z ,total Sˆ z1 S z 2 What are the eigenvalues? 4. Why is distinguishing the two electrons in a helium atom impossible, but distinguishing the two electrons in separate hydrogen atoms possible? Do you think the electrons are distinguishable in the diatomic H2 hy ...
... Lˆ z ,total Lˆ z1 Lˆ z 2 and S z ,total Sˆ z1 S z 2 What are the eigenvalues? 4. Why is distinguishing the two electrons in a helium atom impossible, but distinguishing the two electrons in separate hydrogen atoms possible? Do you think the electrons are distinguishable in the diatomic H2 hy ...
electrons - Portal UniMAP
... space because the volume of the nucleus and the electrons outside the nucleus are extremely small compared to the overall volume of the atom. ...
... space because the volume of the nucleus and the electrons outside the nucleus are extremely small compared to the overall volume of the atom. ...
Atomic orbital
An atomic orbital is a mathematical function that describes the wave-like behavior of either one electron or a pair of electrons in an atom. This function can be used to calculate the probability of finding any electron of an atom in any specific region around the atom's nucleus. The term may also refer to the physical region or space where the electron can be calculated to be present, as defined by the particular mathematical form of the orbital.Each orbital in an atom is characterized by a unique set of values of the three quantum numbers n, ℓ, and m, which respectively correspond to the electron's energy, angular momentum, and an angular momentum vector component (the magnetic quantum number). Any orbital can be occupied by a maximum of two electrons, each with its own spin quantum number. The simple names s orbital, p orbital, d orbital and f orbital refer to orbitals with angular momentum quantum number ℓ = 0, 1, 2 and 3 respectively. These names, together with the value of n, are used to describe the electron configurations of atoms. They are derived from the description by early spectroscopists of certain series of alkali metal spectroscopic lines as sharp, principal, diffuse, and fundamental. Orbitals for ℓ > 3 continue alphabetically, omitting j (g, h, i, k, …).Atomic orbitals are the basic building blocks of the atomic orbital model (alternatively known as the electron cloud or wave mechanics model), a modern framework for visualizing the submicroscopic behavior of electrons in matter. In this model the electron cloud of a multi-electron atom may be seen as being built up (in approximation) in an electron configuration that is a product of simpler hydrogen-like atomic orbitals. The repeating periodicity of the blocks of 2, 6, 10, and 14 elements within sections of the periodic table arises naturally from the total number of electrons that occupy a complete set of s, p, d and f atomic orbitals, respectively.