Lecture Trends in the Periodic Table - NGHS
... degenerate when they have the same energy. The energy of an orbital depends on both its size and its shape because the electron spends more of its time further from the nucleus of the atom as the orbital becomes larger or the shape becomes more complex. In an isolated atom, however, the energy of an ...
... degenerate when they have the same energy. The energy of an orbital depends on both its size and its shape because the electron spends more of its time further from the nucleus of the atom as the orbital becomes larger or the shape becomes more complex. In an isolated atom, however, the energy of an ...
AS Physics
... “Force experienced by hadrons (baryons and mesons)” Weak Force “Force experienced by leptons and hadrons, responsible for changes to quark composition” Electromagnetic Force “Force experienced by charged particles” Gravity “Force experienced by all particles with mass” ...
... “Force experienced by hadrons (baryons and mesons)” Weak Force “Force experienced by leptons and hadrons, responsible for changes to quark composition” Electromagnetic Force “Force experienced by charged particles” Gravity “Force experienced by all particles with mass” ...
05 Chemistry Basics with Flips 2011
... Two atoms can share more than one pair of electrons double bonds (2 pairs of electrons) triple bonds (3 pairs of electrons) ...
... Two atoms can share more than one pair of electrons double bonds (2 pairs of electrons) triple bonds (3 pairs of electrons) ...
Quantum Mechanics: PHL555 Tutorial 2
... Now using center of mass and relative co-ordinate write down the Hamiltonian of the problem in these two coordinates and their conjugate momentum (c) Show that the above problem gets effectively reduced to an one body problem in which an electron is moving around a massive immobile nucleus? Is this ...
... Now using center of mass and relative co-ordinate write down the Hamiltonian of the problem in these two coordinates and their conjugate momentum (c) Show that the above problem gets effectively reduced to an one body problem in which an electron is moving around a massive immobile nucleus? Is this ...
27-3 A Photoelectric Effect Example
... (e) This wavelength is 329 nm, less than the 400 nm (violet) wavelength that marks the lower bound of the visible spectrum. This light is beyond violet, in the ultraviolet. Related End-of-Chapter Exercises: 13 – 16, 43, 44. Essential Question 27.3: With a particular metal plate, shining a beam of re ...
... (e) This wavelength is 329 nm, less than the 400 nm (violet) wavelength that marks the lower bound of the visible spectrum. This light is beyond violet, in the ultraviolet. Related End-of-Chapter Exercises: 13 – 16, 43, 44. Essential Question 27.3: With a particular metal plate, shining a beam of re ...
CHAPTER 1 Practice Exercises 1.1 12.3 g Cd 1.3 26.9814 u 1.5
... Conservation of mass derives from the postulate that atoms are not destroyed in chemical reactions. The Law of Definite Proportions derives from the notion that compounds are always composed of the same types and numbers of atoms of the various elements in the compound. ...
... Conservation of mass derives from the postulate that atoms are not destroyed in chemical reactions. The Law of Definite Proportions derives from the notion that compounds are always composed of the same types and numbers of atoms of the various elements in the compound. ...
2 is
... • Predicts available energy states agreeing with Bohr. • Don’t have definite electron position, only a probability function. • Each orbital can have 0 angular momentum! • Each electron state labeled by 4 numbers: n = principal quantum number (1, 2, 3, …) l = angular momentum (0, 1, 2, … n-1) ml = co ...
... • Predicts available energy states agreeing with Bohr. • Don’t have definite electron position, only a probability function. • Each orbital can have 0 angular momentum! • Each electron state labeled by 4 numbers: n = principal quantum number (1, 2, 3, …) l = angular momentum (0, 1, 2, … n-1) ml = co ...
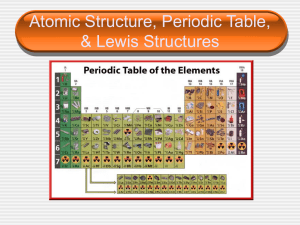
Periodic Table
... All atoms of a given element are ____________ , having the same size, mass, and chemical properties. Atoms of a specific element are ____________ from other elements Atoms cannot be ____________ , ____________ , or ...
... All atoms of a given element are ____________ , having the same size, mass, and chemical properties. Atoms of a specific element are ____________ from other elements Atoms cannot be ____________ , ____________ , or ...
Pretest for Uncertainty Principle Part 1
... 3. Suppose at time t=0, the position space wavefunction for a particle is not given explicitly but its momentum space wavefunction is given. Is it possible to determine the uncertainty in the position of the particle at time t=0 without knowing the Hamiltonian of the system? Explain. ...
... 3. Suppose at time t=0, the position space wavefunction for a particle is not given explicitly but its momentum space wavefunction is given. Is it possible to determine the uncertainty in the position of the particle at time t=0 without knowing the Hamiltonian of the system? Explain. ...
2 - Physics at Oregon State University
... “state” the particle has • Does interact with magnetic fields like L, but not continuous! • NOT a physical rotation • INTRINSIC property – like charge and rest mass! We have no model for what “makes it up/causes it” for fundamental particles • Shows up most simply in Pauli exclusion principle ...
... “state” the particle has • Does interact with magnetic fields like L, but not continuous! • NOT a physical rotation • INTRINSIC property – like charge and rest mass! We have no model for what “makes it up/causes it” for fundamental particles • Shows up most simply in Pauli exclusion principle ...
Review II
... B. Dalton (early 1800's) 1. Each element is composed of tiny indestructible particles called atoms 2. All atoms of a given element have the same mass and other properties that distinguish them from atoms of other elements 3. Atoms combine in simple, whole-number ratios to form compounds -Law of cons ...
... B. Dalton (early 1800's) 1. Each element is composed of tiny indestructible particles called atoms 2. All atoms of a given element have the same mass and other properties that distinguish them from atoms of other elements 3. Atoms combine in simple, whole-number ratios to form compounds -Law of cons ...
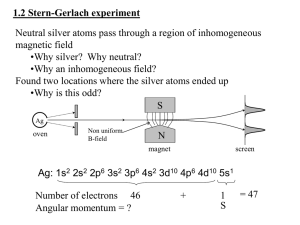
Spectra and atomic structure
... If we look at the spectrum of atomic hydrogen we can see that it is made up of series of lines. This arrangement of lines is unique to hydrogen, other monatomic gases have a line spectrum but no other element shows the same spectrum as hydrogen and it is sensible to suppose that the spectrum somehow ...
... If we look at the spectrum of atomic hydrogen we can see that it is made up of series of lines. This arrangement of lines is unique to hydrogen, other monatomic gases have a line spectrum but no other element shows the same spectrum as hydrogen and it is sensible to suppose that the spectrum somehow ...
Additional Chemistry
... 1. Increase the temperature and it will try to lower it by using the endothermic reaction and visa versa. 2. Increase the pressure and it will make less molecules in order to decrease the pressure again and visa versa. 3. If you add more of anything in the equilibrium it will move the other way to g ...
... 1. Increase the temperature and it will try to lower it by using the endothermic reaction and visa versa. 2. Increase the pressure and it will make less molecules in order to decrease the pressure again and visa versa. 3. If you add more of anything in the equilibrium it will move the other way to g ...
Chem700 MO
... • each orbital sees the average distribution of all the other electrons • finding a many electron wavefunction is reduced to finding a series of one electron orbitals ...
... • each orbital sees the average distribution of all the other electrons • finding a many electron wavefunction is reduced to finding a series of one electron orbitals ...
3.2 Conserved Properties/Constants of Motion
... 2. the operator Lz and ~ being the spin operator. 3. the operator Sz , with S The state of an Hydrogen atom is thus completely defined by the quantum numbers H ...
... 2. the operator Lz and ~ being the spin operator. 3. the operator Sz , with S The state of an Hydrogen atom is thus completely defined by the quantum numbers H ...
Atomic orbital
An atomic orbital is a mathematical function that describes the wave-like behavior of either one electron or a pair of electrons in an atom. This function can be used to calculate the probability of finding any electron of an atom in any specific region around the atom's nucleus. The term may also refer to the physical region or space where the electron can be calculated to be present, as defined by the particular mathematical form of the orbital.Each orbital in an atom is characterized by a unique set of values of the three quantum numbers n, ℓ, and m, which respectively correspond to the electron's energy, angular momentum, and an angular momentum vector component (the magnetic quantum number). Any orbital can be occupied by a maximum of two electrons, each with its own spin quantum number. The simple names s orbital, p orbital, d orbital and f orbital refer to orbitals with angular momentum quantum number ℓ = 0, 1, 2 and 3 respectively. These names, together with the value of n, are used to describe the electron configurations of atoms. They are derived from the description by early spectroscopists of certain series of alkali metal spectroscopic lines as sharp, principal, diffuse, and fundamental. Orbitals for ℓ > 3 continue alphabetically, omitting j (g, h, i, k, …).Atomic orbitals are the basic building blocks of the atomic orbital model (alternatively known as the electron cloud or wave mechanics model), a modern framework for visualizing the submicroscopic behavior of electrons in matter. In this model the electron cloud of a multi-electron atom may be seen as being built up (in approximation) in an electron configuration that is a product of simpler hydrogen-like atomic orbitals. The repeating periodicity of the blocks of 2, 6, 10, and 14 elements within sections of the periodic table arises naturally from the total number of electrons that occupy a complete set of s, p, d and f atomic orbitals, respectively.