* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Spectra and atomic structure
Bremsstrahlung wikipedia , lookup
Atomic orbital wikipedia , lookup
Franck–Condon principle wikipedia , lookup
Wave–particle duality wikipedia , lookup
Particle in a box wikipedia , lookup
Auger electron spectroscopy wikipedia , lookup
Electron configuration wikipedia , lookup
Tight binding wikipedia , lookup
Mössbauer spectroscopy wikipedia , lookup
Rutherford backscattering spectrometry wikipedia , lookup
Theoretical and experimental justification for the Schrödinger equation wikipedia , lookup
X-ray photoelectron spectroscopy wikipedia , lookup
X-ray fluorescence wikipedia , lookup
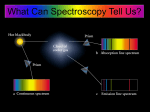
SPECTRA OF THE ELEMENTS So far we have thought about the radiation emitted by hot solids but we are now going to broaden it by considering gases. Looking at light emitted by a source through a prism or a diffraction grating can tell us a great deal, not only what the substance is but also much about its atomic structure! Emission spectra You should have a look at various spectra (some of which are shown in the photographs). You will see that they fall into roughly three groups. (i) Line spectra - these are emitted from hot monatomic gases - the atoms are not linked to each other in any way. (ii) Band spectra - these are emitted by gases as well but from ones with more than one atom per molecule. (iii) Continuous spectra - these are emitted from hot solids - the intensity /wavelength distribution depending on the temperature of the solid. Absorption spectrum This type of spectrum is formed by the passage of light through a cooler vapour. The vapour then absorbs those regions of the spectrum which it would have emitted had it been in an excited state. In the cooler gas most of the atoms are in the ground state (the lowest possible energy state). Absorption occurs when the electrons in the atoms absorb energy from the incoming radiation and then reradiate it in all directions. In 1814 Fraunhofer discovered that the spectrum of the Sun’s radiation was crossed by hundreds of absorption lines which are called Fraunhofer lines. These are due to the absorption of light from the centre of the Sun by the outer and cooler layers. Study of these lines gives the astronomers a way of determining the composition of the Sun. One of the simplest of spectra to explain is that of hydrogen and it is what we will consider next 1 SPECTRA - THE KEY TO ATOMIC STRUCTURE If we look at the spectrum of atomic hydrogen we can see that it is made up of series of lines. This arrangement of lines is unique to hydrogen, other monatomic gases have a line spectrum but no other element shows the same spectrum as hydrogen and it is sensible to suppose that the spectrum somehow reflects the atomic structure of the atom that produced it. Now in 1913 Neils Bohr suggested that the energy of an electron in a hydrogen atom is quantised - that is the energy can only have certain values. Each level is given a quantum number. When energy is given to the atom an electron can jump up from one level to a higher level. This transition will only take place if the energy provided is equal to the difference in energy between the two levels. Energy level Electron transition Energy may be supplied as either: (a) radiation (b) electrical (c) a particle beam or (d) heat When an electron drops from one level to another a quantum of radiant energy is emitted and this gives a line in the hydrogen spectrum. The energy of this quantum is given by the formula: Quantum energy: E = hf where h is Planck’s constant and f is the frequency The bigger the energy difference the greater the energy of the emitted quantum and therefore the higher its frequency. Bohr actually derived a formula giving the energy of these levels and using it we can calculate the values for the hydrogen atom shown in the diagram and the following table. Bohr’s formula was: Energy of level n = 13.6/n2 eV. n 1 2 3 4 5 6 Energy (eV) -13.6 -3.4 -1.51 -0.85 -0.54 -0.38 Energy (J) -21.8x10-19 -5.44x10-19 -2.42x10-19 -1.36x10-19 -0.87x10-19 -0.60x10-19 The energy level for n = 1 is called the ground state. Energy levels with n = 2 and above are called excited states and the level with n = ∞ is known as the ionisation state. Notice that all the energies are negative compared with the ionisation state which has zero energy. This means that an electron in any of the other levels has to gain a certain amount of energy to reach the ionisation level and so escape from the atom. 2