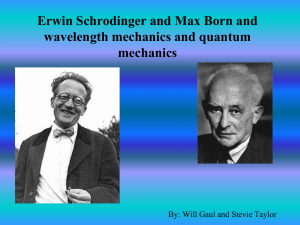Quantum Mechanics II, Ex 4730
... Submitted by: Roee Steiner 034744821 Given a spherical shell with radius R and a particle with mass M and charge e. Notice that the standard variables which show the particle are (θ, φ, Lx, Ly, Lz) In this question we have to assume that the particle can be excited from ground state to first energy ...
... Submitted by: Roee Steiner 034744821 Given a spherical shell with radius R and a particle with mass M and charge e. Notice that the standard variables which show the particle are (θ, φ, Lx, Ly, Lz) In this question we have to assume that the particle can be excited from ground state to first energy ...
Atomic Structure and Quantum Theory
... the energy is not continuous but rather quantized… quantum mechanics was born ...
... the energy is not continuous but rather quantized… quantum mechanics was born ...
Problem statement: Solution: Let`s note that is not a solution. That
... Substituting in the original equation we see that this solution satisfies the conditions given. Special thanks to AOPS member obi1kenobi for helping solve this problem. ...
... Substituting in the original equation we see that this solution satisfies the conditions given. Special thanks to AOPS member obi1kenobi for helping solve this problem. ...
CCR 29: Reduced Mass
... mass (CM) of the system moves at constant velocity and, without any loss of generality, we can locate the coordinate origin at the center of mass (see Figure RM-1). That allows us to write m 1r1 + m 2r2 = 0 ...
... mass (CM) of the system moves at constant velocity and, without any loss of generality, we can locate the coordinate origin at the center of mass (see Figure RM-1). That allows us to write m 1r1 + m 2r2 = 0 ...
Bohr`s equation for the hydrogen atom Bohr derived an equation to
... Every electron within an atom is considered to have four quantum numbers: (a) the principal quantum number (n), representing the energy level; (b) the orbital quantum number (L), which may have any integral value between 0 and n -1; (c) the magnetic quantum number (m), which may have any integral va ...
... Every electron within an atom is considered to have four quantum numbers: (a) the principal quantum number (n), representing the energy level; (b) the orbital quantum number (L), which may have any integral value between 0 and n -1; (c) the magnetic quantum number (m), which may have any integral va ...
Lecture 8 1 Planck-Einstein Relation E = hν 2 Time evolution of real
... This relation was first proposed by Planck in 1900 to explain the properties of black body radiation. The interpretation was that matter energy levels are quantized. At the time this appeared compatible with the notion that matter is composed of particles that oscillate. The discovery that the energ ...
... This relation was first proposed by Planck in 1900 to explain the properties of black body radiation. The interpretation was that matter energy levels are quantized. At the time this appeared compatible with the notion that matter is composed of particles that oscillate. The discovery that the energ ...
Lecture.1.part1
... Charge (Q) is a quantity we have defined in order to describe how certain particles (with this charge) interact. If the particles don’t interact in the prescribed way, they don’t have charge. The force, F, between two charges (and the classical mathematical model, Coulomb’s Law, kQ1Q2/r2), was deriv ...
... Charge (Q) is a quantity we have defined in order to describe how certain particles (with this charge) interact. If the particles don’t interact in the prescribed way, they don’t have charge. The force, F, between two charges (and the classical mathematical model, Coulomb’s Law, kQ1Q2/r2), was deriv ...
Particle on a Sphere
... Spherical Polar Coordinates = most efficient way to describe position of particle on sphere ...
... Spherical Polar Coordinates = most efficient way to describe position of particle on sphere ...
pdf
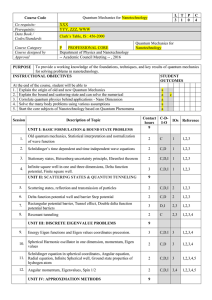
... 1. Explain the origin of old and new Quantum Mechanics a 2. Explain the bound and scattering state and can solve the numerical a c 3. Correlate quantum physics behind applications - Nano Dimension a 4. Solve the many body problems using various assumptions a 5. Start the core subjects of Nanotechnol ...
... 1. Explain the origin of old and new Quantum Mechanics a 2. Explain the bound and scattering state and can solve the numerical a c 3. Correlate quantum physics behind applications - Nano Dimension a 4. Solve the many body problems using various assumptions a 5. Start the core subjects of Nanotechnol ...