Final Exam Review
... 43. What is in the nucleus of an atom? 44. Write the orbital diagram & electron configurations for the following elements: K, Ar, H, He, Br 45. Define precision and accuracy. 46. What determines an element’s order on the periodic table? 47. What happens to the temperature of a substance as it is cha ...
... 43. What is in the nucleus of an atom? 44. Write the orbital diagram & electron configurations for the following elements: K, Ar, H, He, Br 45. Define precision and accuracy. 46. What determines an element’s order on the periodic table? 47. What happens to the temperature of a substance as it is cha ...
Quantum Numbers (6.5-9)
... The magnetic quantum number, ml, defines the orientation of the orbital in which the electron inhabits. The number of ml values is called the degeneracy, or the number of orbitals in the atom that are at the same energy level. Note that to have the same energy, the orbitals must be on the same energ ...
... The magnetic quantum number, ml, defines the orientation of the orbital in which the electron inhabits. The number of ml values is called the degeneracy, or the number of orbitals in the atom that are at the same energy level. Note that to have the same energy, the orbitals must be on the same energ ...
Quantum Numbers
... The magnetic quantum number, ml, defines the orientation of the orbital in which the electron inhabits. The number of ml values is called the degeneracy, or the number of orbitals in the atom that are at the same energy level. Note that to have the same energy, the orbitals must be on the same energ ...
... The magnetic quantum number, ml, defines the orientation of the orbital in which the electron inhabits. The number of ml values is called the degeneracy, or the number of orbitals in the atom that are at the same energy level. Note that to have the same energy, the orbitals must be on the same energ ...
Chapter 2 - Speedway High School
... protons but may differ in number of neutrons • some are radioactive ...
... protons but may differ in number of neutrons • some are radioactive ...
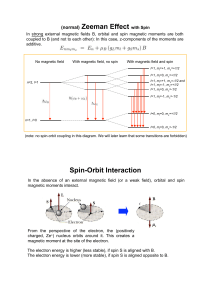
(normal) Zeeman Effect with Spin Spin
... 2s+1 : “Spin Multiplicity” " total number of spin states [e.g. 2s+1=2 (up and down) for s=1/2]. ...
... 2s+1 : “Spin Multiplicity” " total number of spin states [e.g. 2s+1=2 (up and down) for s=1/2]. ...
Chapter 7(Hill/Petrucci/McCreary/Perry Introduction to Atomic
... λ = (h/mv) for particle of mass = m and speed = v, where h = 6.626 x 10-34 J s Ordinary objects have wavelengths too short to be observed … e.g. a 98 mph baseball …only 1.1 x 10-25 nm. We use small particles like electrons and neutrons instead of visible light when we want to look at very small obje ...
... λ = (h/mv) for particle of mass = m and speed = v, where h = 6.626 x 10-34 J s Ordinary objects have wavelengths too short to be observed … e.g. a 98 mph baseball …only 1.1 x 10-25 nm. We use small particles like electrons and neutrons instead of visible light when we want to look at very small obje ...
7.4 The Quantum-Mechanical Model of the Atom
... • The solutions for the wavefunction, Ψ, in the H atom are called atomic orbitals • Born’s interpretation of the wavefunction – the probability to find the electron at a certain point (x, y, z) in space is proportional to the square of the wave function, Ψ2, in this point • Electron density diagrams ...
... • The solutions for the wavefunction, Ψ, in the H atom are called atomic orbitals • Born’s interpretation of the wavefunction – the probability to find the electron at a certain point (x, y, z) in space is proportional to the square of the wave function, Ψ2, in this point • Electron density diagrams ...
The Bohr Model of the Hydrogen Atom
... at one radius, however; electrons can make a “jump” from one orbit to another essentially instantaneously. The electrons are forced to jump to a higher orbit if it absorbs just the right amount of energy (in the form of light) to raise its energy up to equal that necessary to orbit in the next level ...
... at one radius, however; electrons can make a “jump” from one orbit to another essentially instantaneously. The electrons are forced to jump to a higher orbit if it absorbs just the right amount of energy (in the form of light) to raise its energy up to equal that necessary to orbit in the next level ...
Chemistry Week 04 - nchsdduncanchem1
... No two electrons in an atom have the same set of four quantum numbers. Hund's Rule: Electrons will enter empty orbitals of equal energy, when they are available. Quantum Chemistry: Describes the way atoms combine to form molecules and the way molecules interact with one another, using the rules of q ...
... No two electrons in an atom have the same set of four quantum numbers. Hund's Rule: Electrons will enter empty orbitals of equal energy, when they are available. Quantum Chemistry: Describes the way atoms combine to form molecules and the way molecules interact with one another, using the rules of q ...
Part One: Light Waves, Photons, and Bohr Theory A. The Wave
... Bohr Frequency Rule: The atom can only absorb or emit light having just the right energy (and thus frequency or wavelength) to move the e- between these energy levels. ...
... Bohr Frequency Rule: The atom can only absorb or emit light having just the right energy (and thus frequency or wavelength) to move the e- between these energy levels. ...
Light and Energy AP Style
... Only for hydrogen atoms and other monoelectronic species. Why the negative sign? To increase the energy of the electron you make it further to the nucleus. the maximum energy an electron can have is zero, at an infinite distance. ...
... Only for hydrogen atoms and other monoelectronic species. Why the negative sign? To increase the energy of the electron you make it further to the nucleus. the maximum energy an electron can have is zero, at an infinite distance. ...
MSE 221 Quantum Physics of Materials
... MSE 221 Quantum Physics of Materials Elementary quantum concepts, wave mechanics, energy states, bonding, transitions, electronic properties Prerequisite: PHYS 151 14 weeks, lectures (3 times a week), recitation (once a week) Introduction Old Quantum Theory, Bohr model, De Broglie, duality Interfere ...
... MSE 221 Quantum Physics of Materials Elementary quantum concepts, wave mechanics, energy states, bonding, transitions, electronic properties Prerequisite: PHYS 151 14 weeks, lectures (3 times a week), recitation (once a week) Introduction Old Quantum Theory, Bohr model, De Broglie, duality Interfere ...
Bohr`s model of atom- postulates The electron in an atom moves
... 1.The wavelength range of the visible spectrum extends from violet (400 nm) to red (750 nm). Express these wavelengths in frequencies (Hz). (1nm = 10–9 m) 2.Calculate energy of one mole of photons of radiation whose frequency is 5x1014 Hz. 3.What are the frequency and wavelength of a photon emitted ...
... 1.The wavelength range of the visible spectrum extends from violet (400 nm) to red (750 nm). Express these wavelengths in frequencies (Hz). (1nm = 10–9 m) 2.Calculate energy of one mole of photons of radiation whose frequency is 5x1014 Hz. 3.What are the frequency and wavelength of a photon emitted ...
The Vibrating String
... white light is viewed through a diffraction grating, a continuous spectrum will be produced. ► It looks like this ...
... white light is viewed through a diffraction grating, a continuous spectrum will be produced. ► It looks like this ...
atom
... 5. Four quantum numbers (n, l, ml, ms) ---determine the state of an electron. (1) Principle quantum number n(n=1,2,)--determine the energy of the atom system. (2) azimuthal l(l=0,1,2,,n-1)---determine the magnitude of orbital angular momentum of an electron. (3) magnetic ml(ml=0,1,2,,l) ...
... 5. Four quantum numbers (n, l, ml, ms) ---determine the state of an electron. (1) Principle quantum number n(n=1,2,)--determine the energy of the atom system. (2) azimuthal l(l=0,1,2,,n-1)---determine the magnitude of orbital angular momentum of an electron. (3) magnetic ml(ml=0,1,2,,l) ...
Dr. Vikram Panchal Institute Of Chemistry CH-2 Worksheet: -2
... photon detector receives a total of 3.15 x 10-18 J from the radiations of 600 nm. Calculate the number of photons received by the detectors. 8. Given this set of quantum numbers for a multi-electron atom 2, 0, 0,1/2 and 2,0,0,-1/2. What is the next highest allowed set of ‘n’ and ‘l’quantum numbers f ...
... photon detector receives a total of 3.15 x 10-18 J from the radiations of 600 nm. Calculate the number of photons received by the detectors. 8. Given this set of quantum numbers for a multi-electron atom 2, 0, 0,1/2 and 2,0,0,-1/2. What is the next highest allowed set of ‘n’ and ‘l’quantum numbers f ...
ARRANGEMENT OF ELECTRONS IN ATOMS
... - The distance between any 2 corresponding points on one of these water waves, such as from crest to crest, is the wave’s ________________________________, . We can measure the waves’ frequency, v, by observing how often the ___________________________________rises and falls at a given point, such ...
... - The distance between any 2 corresponding points on one of these water waves, such as from crest to crest, is the wave’s ________________________________, . We can measure the waves’ frequency, v, by observing how often the ___________________________________rises and falls at a given point, such ...
Midterm Exam 2
... Section 1- Concepts and Definitions (50% 5 points each) 1) Give two examples of a hydrogenic atom other than hydrogen (H): ...
... Section 1- Concepts and Definitions (50% 5 points each) 1) Give two examples of a hydrogenic atom other than hydrogen (H): ...
4. - period2chem
... Hydrogen atoms have specific energy levels. Therefore, the atoms can only gain or lose certain amounts of energy. When atoms lose energy, they emit photons which correspond to the lines in the emission spectrum. The more energy lost, the more energy the photon has. Bohr’s model stated that electrons ...
... Hydrogen atoms have specific energy levels. Therefore, the atoms can only gain or lose certain amounts of energy. When atoms lose energy, they emit photons which correspond to the lines in the emission spectrum. The more energy lost, the more energy the photon has. Bohr’s model stated that electrons ...
Bohr model
In atomic physics, the Rutherford–Bohr model or Bohr model, introduced by Niels Bohr in 1913, depicts the atom as a small, positively charged nucleus surrounded by electrons that travel in circular orbits around the nucleus—similar in structure to the solar system, but with attraction provided by electrostatic forces rather than gravity. After the cubic model (1902), the plum-pudding model (1904), the Saturnian model (1904), and the Rutherford model (1911) came the Rutherford–Bohr model or just Bohr model for short (1913). The improvement to the Rutherford model is mostly a quantum physical interpretation of it. The Bohr model has been superseded, but the quantum theory remains sound.The model's key success lay in explaining the Rydberg formula for the spectral emission lines of atomic hydrogen. While the Rydberg formula had been known experimentally, it did not gain a theoretical underpinning until the Bohr model was introduced. Not only did the Bohr model explain the reason for the structure of the Rydberg formula, it also provided a justification for its empirical results in terms of fundamental physical constants.The Bohr model is a relatively primitive model of the hydrogen atom, compared to the valence shell atom. As a theory, it can be derived as a first-order approximation of the hydrogen atom using the broader and much more accurate quantum mechanics and thus may be considered to be an obsolete scientific theory. However, because of its simplicity, and its correct results for selected systems (see below for application), the Bohr model is still commonly taught to introduce students to quantum mechanics or energy level diagrams before moving on to the more accurate, but more complex, valence shell atom. A related model was originally proposed by Arthur Erich Haas in 1910, but was rejected. The quantum theory of the period between Planck's discovery of the quantum (1900) and the advent of a full-blown quantum mechanics (1925) is often referred to as the old quantum theory.