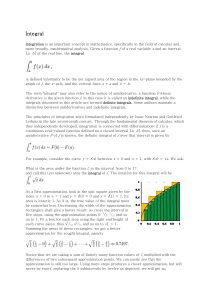
Quantum mechanics of a free particle from properties of the Dirac
... of a sequence of functions). The delta function is a distribution, that is, a linear continuous functional defined on the space of “good” functions.16 Even though this definition might not be very appealing at first sight, it leads to consistent and fruitful mathematics.16 The theory of distribution ...
... of a sequence of functions). The delta function is a distribution, that is, a linear continuous functional defined on the space of “good” functions.16 Even though this definition might not be very appealing at first sight, it leads to consistent and fruitful mathematics.16 The theory of distribution ...
4 Time evolution - McMaster Physics and Astronomy
... On the LHS I put the time dependence together with as a way to remember that this state depends on time. On the RHS I only made the coefficient time dependent, because the eigenstates of the ẑ-spin operator, namely |"z i and |#z i do not depend on time. So really what we are after is to understand ...
... On the LHS I put the time dependence together with as a way to remember that this state depends on time. On the RHS I only made the coefficient time dependent, because the eigenstates of the ẑ-spin operator, namely |"z i and |#z i do not depend on time. So really what we are after is to understand ...
There are 4 quantum numbers. - 12S7F-note
... The angular momentum number [l] is the orbital of the electron i.e. the s-orbital is represented by 0, the p-orbital by 1, the d-orbital by 2 and so on. The magnetic quantum number [ml] is the sub-orbital or cloud of the electron. It ranges from –l to l. The spin projection quantum number [ms] is th ...
... The angular momentum number [l] is the orbital of the electron i.e. the s-orbital is represented by 0, the p-orbital by 1, the d-orbital by 2 and so on. The magnetic quantum number [ml] is the sub-orbital or cloud of the electron. It ranges from –l to l. The spin projection quantum number [ms] is th ...
Document
... Equation and Quantum Numbers There are four different quantum numbers needed to specify the state of an electron in an atom. 1. The principal quantum number n gives the total energy. 2. The orbital quantum number gives the angular momentum; can take on integer values from 0 to n - 1. ...
... Equation and Quantum Numbers There are four different quantum numbers needed to specify the state of an electron in an atom. 1. The principal quantum number n gives the total energy. 2. The orbital quantum number gives the angular momentum; can take on integer values from 0 to n - 1. ...
Igor Volovich
... Liouville equation for the distribution function of particles in a finite volume, derive a chain of equations for the distribution functions, pass to the infinite-volume, infinite number of particles limit, postulate that the initial correlations between the particles were weaker in the remote past, ...
... Liouville equation for the distribution function of particles in a finite volume, derive a chain of equations for the distribution functions, pass to the infinite-volume, infinite number of particles limit, postulate that the initial correlations between the particles were weaker in the remote past, ...
Introduction: what is quantum field theory ?
... annihilated) - the particle number is not conserved. This fact is demonstrated at a daily basis in CERN and other accelerators. It is a direct consequence of the combination of quantum mechanics and special relativity. Particles are not indestructible objects, made at the beginning of the universe a ...
... annihilated) - the particle number is not conserved. This fact is demonstrated at a daily basis in CERN and other accelerators. It is a direct consequence of the combination of quantum mechanics and special relativity. Particles are not indestructible objects, made at the beginning of the universe a ...
The statistical interpretation of quantum mechanics
... in the limiting case where the numbers of the stationary states, the so-called quantum numbers, are very large (that is to say, far to the right and to the lower part in the above array) and the energy changes relatively little from place to place, in fact practically continuously. Theoretical physi ...
... in the limiting case where the numbers of the stationary states, the so-called quantum numbers, are very large (that is to say, far to the right and to the lower part in the above array) and the energy changes relatively little from place to place, in fact practically continuously. Theoretical physi ...
Relativity Problem Set 9
... state energy E0 , find the constant B. (b) Find the constant A by imposing the normalization of the wave function. ...
... state energy E0 , find the constant B. (b) Find the constant A by imposing the normalization of the wave function. ...
Quantum Mechanics: Vibration and Rotation of Molecules
... integer or zero. There are sets of polynomials such that the product of any two different ones, multiplied by a function w(x) called a weight function and integrated over a certain interval, vanishes. Such a set is called a set of orthogonal polynomials. Among other things, this makes it possible to ...
... integer or zero. There are sets of polynomials such that the product of any two different ones, multiplied by a function w(x) called a weight function and integrated over a certain interval, vanishes. Such a set is called a set of orthogonal polynomials. Among other things, this makes it possible to ...
Effective Hamiltonians and quantum states
... In §2, I derive two elementary identities connecting the quantities u, σ, s and a as above. These formulas record by how much the quantum state ψ fails to minimize the classical action. ...
... In §2, I derive two elementary identities connecting the quantities u, σ, s and a as above. These formulas record by how much the quantum state ψ fails to minimize the classical action. ...