Download An even degree function with

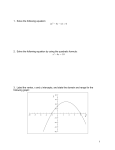
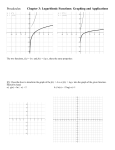
Advanced Functions
3.2 Graphing Polynomial Functions
Name____________________ Date ______
A polynomial function is a function of the form:
f(x) = anxn + an−1xn−1 + . . . + a1x + a0
What are an , an−1 ,
...,
a1 , a0 ? _______________
What are n, n-1, n-2, … ? ________________
Note: all coefficients must be real numbers and all exponents of variables must be whole numbers!!
3
2
Example: 2x  5x  4x  7
Name the leading coefficient________, the constant_________, and the degree_________,
the linear term __________, the quadratic term __________.
Give an example of each type of quadratic:
Degree
Type
Constant
Linear
Quadratic
Cubic
Quartic
Standard Form
Some graphing fun.
Sketch (general shape . . . .) each function:
f(x) = 2x
f(x) = x3
f(x) = 2x3 + 1
f(x) = 4x5+7x4 –5x3–9x2+x+4
f(x) = −x3
f(x) = −2x3 + 1
f(x) = -4x5+7x4 –5x3–9x2+x+4
Now, repeat:
f(x) = −2x
What happened to the leading coefficient? What happened to the graph?
Sketch again:
f(x) = 2x2
f(x) = x2 + 3
f(x) = x4
f(x) = 2x4 + 1
f(x) = −x2 + 3
f(x) = −x4
f(x) = −2x4 + 1
Now, repeat:
f(x) = −2x2
What happened to the leading coefficient? What happened to the graph?
Now, to organize your findings, provide a sketch for each description.
An odd degree function with
an > 0
an < 0
An even degree function with
an > 0
an < 0
We have to be more technical with these descriptions.
First, definitions:
x → +∞
x approaches positive infinity (x gets large)
x → −∞
x approaches negative infinity (x gets small)
Odd degree function
an> 0
an< 0
x → −∞
x → +∞
f(x) → −∞
f(x) → +∞
f(x) → +∞
f(x) → −∞
Even degree function
an> 0
an< 0
x → −∞
x → +∞
f(x) → +∞
f(x) → +∞
f(x) → −∞
f(x) → −∞
What if you didn’t have a calculator to graph?
Graph f(x) = 2x4 + 1
x
1st- What are your end behaviors?
2nd – Make an x/y chart and fill in some values
3rd – Plot the graph
y
Review:
1) Write the slope-intercept form of the equation of the line passing through
4,  4 and 5,  10 .


2) Graph the following:


f ( x)  x  5  2
3) Identify the interval over which the graph of
f (x) is increasing.