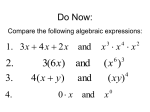* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download the exponent laws
Survey
Document related concepts
Transcript
MPM2D WORKING WITH EXPONENTS Exponents are a simpler way of showing a repeated multiplication. Powers are products of equal factors. They can be written in expanded form or exponential form. 3 x 3 x 3 x 3 x 3 x 3 x 3 x 3 can also be written as 38 the entire expression is called a POWER 38 the number 8 is the EXPONENT, it tells us the number of times the base has been repeated the number 3 is the BASE, it tells us the number that is being multiplied by itself THE EXPONENT LAWS Example 1: Multiply (4)3 (4)2 if we expand (4)3(4)2 Notice - the bases are the same it means (4 x 4 x 4) (4 x 4) = 45 Example 2: Multiply (x)4 (x)2 if we expand = (x)(x)(x)(x) (x)(x) Example 3: Multiply (x2y3)(x3y4) if we expand = (x)(x)(y)(y)(y) = (x)6 (x)(x)(x)(y)(y)(y)(y) = (x)5(y)7 LAW #1: MULTIPLICATION OF POWERS To multiply powers with the same base, add the exponents and keep the base the same (x)m (x)n = x m+n Example 4: Divide (4)5 ÷ (4)2 Example 5: Divide (x4) ÷ (x)2 (4)( 4)( 4)( 4)( 4) (4)( 4) if we expand = reduce = (4)3 = ( x)( x)( x)( x) ( x)( x) = (x)2 Example 6: Divide (x3y4) ÷ (x2y2) if we expand = reduce = xy2 ( x)( x)( x)( y )( y )( y )( y ) ( x)( x)( y )( y ) LAW #2: DIVISION OF POWERS To divide powers, subtract the exponents and keep the base (x)m ÷ (x)n = x m-n Example 7: Expand (53)2 If we expand = (53)(53) = (x2y3)(x2y3)(x2y3) simplify = 56 = x6y9 Example 8: Expand (x2y3)3 3 Example 9: Expand If we expand simplify x2 2 y x 2 x 2 = 2 2 y y x6 = 6 y x 2 2 y POWER OF A QUOTIENT LAW POWER OF A POWER LAW To apply a power to a power, multiply the exponents and keep the base the same (xm)n = xmn To apply a power to a quotient, multiply the exponents in both the numerator and the denominator, keep the base the same. xm m y n x mn mn y ZERO AND NEGATIVE EXPONENTS We can use the patterns and the basic laws of exponents to understand the meaning of zero and negative exponents. 43 ÷ 4 3 Example 1: Simplify 43 ÷ 43 4 4 4 = 4 4 4 =1 43 ÷ 43 but also = 4 3-3 = 40 therefore, 40 = 1 Example 2: Simplify 42 ÷ 45 42 ÷ 45 42 ÷ 45 but also 4 4 4 4 4 4 4 1 = 4 4 4 1 = 3 4 = 4 2-5 = therefore, 4-3 = = 4 –3 1 43 NEGATIVE EXPONENTS Any power with a negative exponent can be expressed in an equivalent fraction form with a positive exponent 1 n x5-B-2 n x **Exponents change their sign if they move from numerator to denominator OR from denominator to numerator! Always try to express answers with positive exponents only!** Eg. 1 = 43 4 3 and x 2 y 3 5 6 = x y EXPONENT WORKSHEET Use the exponent laws we’ve learned to find the following: 1) State the following numbers as powers of 2 a) 16 _______ b) 2 d) (28)(27) _________ _______ c) 32 e) 2 x 29 ________ f) _________ 28 _________ 24 g) 4 x 32 _________ (hint: change to same base) h) 4 x 8 _________ 2) State the following numbers as powers of 3 a) 27 d) 34 _______ 35 x _________ b) 243 _________ c) 38 x 3 __________ 35 e) 2 3 32 f) 5 3 ________ __________ g) 27 x 81 _________ 3) Simplify the following expressions a) (3x ) 3 3 d) f) _________ 710 712 7 6 7 3 9 2 n 2 4 n1 8n b) 3x 6 4x ____________ 3 x2 c) 4 y __________ ( x m n )( x 2 m ) e) xn 3 ________ _____________ ____________ (hint: change to the same base) 4) Simplify the following expressions 2 x y 8 x y x y 2 a) 4 3 2 5 2 3 __________ b) 2 xy 4 15 x 2 y 3 3x 2 y 2 12 x 4 y 2 _____________ c) 2 n 4 n 1 8 3n 2 16 2 n 1 (HINT: express each with a base of 2) 5) State the following using only positive exponents a) x 8 ________ b) x 2 y 2 1 2 1 ________ e) g) 3 2 ________ h) (-3 x 2 y 2 )( 4 x 2 y 2 ) _________ d) 1 3 1 _________ _________ c) a 3 b 4 ________ 1 2 3 ________ f) 6) Evaluate the following a) 50 _______ 1 d) 2 3 4 f) 0 3 8 (express with same base) h) 5-1 + 5-2 (careful!) c) (3-2)-2 ________ 2 3 2 2 27 2 g) 2-1 + 3-1 b) 4-2 _________ _________ e) 2 5 __________