Download 2. 4. 4 Sample size estimation for a comparison of two means

Topic 2. Distributions, hypothesis testing, and sample size
determination
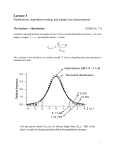
The Student - t distribution (ST&D pg 56 and 77)
Consider a repeated drawing of samples of size n = 5 from a normal distribution.
For each sample compute Y , s, sY , and another statistic, t:
t (n-1)= ( Y - )/ s
Y
(Remember Z = ( Y - )/  Y )
The t statistics is the number of standard error that separate Y and its hypothesized
mean µ.
df=n-1=4
Critical values for |t|>|Z| -> less sensitivity.
This is the price we pay for being
uncertain about the population variance
Fig. 1. Distribution of t (df=4) compared to Z. The t distribution is symmetric, but wider
and flatter than the Z distribution, lying under it at the center and above it in the tails.
1
When N increases the t distribution tend towards the N distribution
2
2. 2. Confidence limits based on sample statistics (ST&D p.77)
The general formula for any parameter  is:
Estimated   Critical value * Standard error of the estimated 
So, for a population mean estimated via a sample mean:
  Y  t
2
, n 1
 sY
The statistic Y is distributed about  according to the t distribution so it satisfies
P{ Y - t /2, n-1
sY
   Y + t /2, n-1 s }= 1- 
Y
For a confidence interval of size 1-, use a t value corresponding to  /2.
Therefore the confidence interval is
Y-
t /2, n-1
sY
   Y + t /2, n-1
sY
These two terms represent the lower and upper 1-  confidence limits of the
mean. The interval between these terms is called confidence interval (CI).
Example: Data Set 1 of Hordeum 14 malt extraction values
Y = 75.94 sY = 1.23 /
14 = 0.3279 A table gives the t0.025,13 value of 2.16
95% CI for  = 75.94 ± 2.160 * 0.3279  [75.23- 76.65]
If we repeatedly obtained samples of size 14 from the population and constructed
these limits for each, we expect 95% of the intervals to contain the true mean.
True mean
Fig. 2 Twenty 95% confidence intervals. One out of 20 intervals does not include
the true mean.
3
2. 3. Hypothesis testing and power of the test (ST&D 94).
Example Barley data. Y = 75.94, sY = s 2 / n = 0.3279, t0.025,13 = 2.160, CI: [75.23- 76.65]
1) Choose a null hypothesis: Test Ho  = 78 against the H1   78.
2) Choose a significance level: Assign  = 0.05
3) Calculate the test statistic t:
Y   75.94  78.00
t
sY

0.3279
 6.28
(interpretation: the sample mean is 6.3 SE from the hypothetical mean of 78. Too far!).
4) Compare the absolute value of the test statistic to the critical statistic:
| - 6.28 | > 2.16
5) Since the absolute value of the test statistic is larger, we reject H0.
This is equivalent to calculate a 95% confidence interval for the mean.
Since o (78) is not within the CI [75.23- 76.65] we reject Ho.
is called the significance level of the test (<0.05): probability of incorrectly
rejecting a true Ho, a Type I error.
is the Type II error: to incorrectly accept Ho when it is false 
Accepted
Null hypothesis
Rejected
True Correct decision
Type I error= 
False Type II error=
Correct decision= Power= 1-
Null hypothesis
Power of the test: 1- is the power of the test, and represents the probability of
correctly rejecting a false null hypothesis. It is a measure of the ability of the test
to detect an alternative mean or a significant difference when it is real
Note that for a given Y and s, if 2 of the 3 quantities , , and n are specified then
the third one can be determined.
Choose the right number of replications to keep Type I error  and Type II error
 under the desired limits (e.g.  <0.05 & <0.20).
4
Power of a test (ST&D pg 118-119)
Power  1    P( Z  Z  / 2 
1   0
Y
) or P(t  t / 2 
1   0
sY
)
 between 2
means in SE
units
What is the power of a test for Ho: = 74.88 in the barley data set against H1:  =
75.94. Since  = 0.05, n = 14 (t 0.025,13 = 2.160), and sY = 0.32795.
Power  1    P(t  2.160 
75.94  74.88
0.32795
)  P(t  1.072)  0.85
The probability of the Type II error  we are looking for is the shaded area to the
left of the lower curve.
/2
Ho is true
Fig. 3. Type I and Type II
errors in the Barley
data set.
Ho is false

Acceptance
1-
Rejection
The area 1- in the
rejection region = the
probability that > 75.588 under H1 = power =
P(t>(75.588-75.94)/0.32795)= P(t>-1.072)=0.85 same as above!
The magnitude of 
1. The Type I error rate 
2. The distance between the two means under consideration
3. The number of observations (n)  sY 
s
n
5
When the distance between the two means is reduced, 
Variation of power as a function of the distance between the
alternative hypotheses (Biometry Sokal and Rohlf)
n=35
SE=0.7
n=5
SE=1.7
6
2.3.2. Power of the test for the difference between the means of two samples
Two types of alternative hypothesis
H0: 1 - 2=0 versus H1: 1 - 2  0 (two tail test) -> (t value: top t Table)
H1: 1 - 2 >0 (one tail test) -> (t value: bottom t Table)
The general power formula for both equal and unequal sample sizes reads as:
Power  P(t  t  
2
| 1   2 |
|   2 |
)  P(t  t   1
)
2
sY 1Y 2
s pooled ,
2
N
where s 2pooled is a weighted variance given by: s 2pooled 
and N 
(n1  1) s12  (n2  1) s 22
(n1  1)  (n2  1)
n1 n2
.
n1  n2
When n1 = n2 = n (equal sample sizes) that the formulas reduce to:
s
2
pooled
(n1  1) s12  (n2  1) s 22 (n  1)( s12  s 22 ) s12  s 22



(n1  1)  (n2  1)
2(n  1)
2
n1 n2
n2 n
N


n1  n2 2n 2
Power  P(t  t  
2
| 1   2 |
|   2 |
)  P(t  t   1
)
2
sY 1Y 2
2
s
2
pooled
n
The variance of the difference between two random variables is the sum of
the variances (error are always added) (ST&D 113-115).
The degrees of freedom for the critical t /2 are
General case: (n1-1) + (n2-1)
Equal sample size: 2*(n-1)
7
2. 4. 2 Sample size for estimating µ, when is known.
Using the z statistic
If the population variance  is known the Z statistic may be used.
Z
Y

so
CI =
Y  Z / 2 Y
or
Y  Z / 2 
n
The formula for d= half-length of the confidence interval for the mean is
[ d
Y
d
]
d  Z  Y  Z
2
2

n
This can be rearranged to estimate the confidence interval in terms of the
population variance. For =0.05:
n = z 2/2 2 / d2 = z 2/2 (/d)2 = (1.96)2(/d)2= 3.8(/d)2
So if d=  n 4
d= 0.5   n 16
d= 0.25   n 64
2
The equation may be expressed in terms
of the coefficient of variation
 
 
2  
n  Z
 Z 2
2
2  d 
2
 

CV 2
d 
 

2
CV= s / Y (as a proportion not as a %)
d/ is the confidence interval as a fraction of the population mean.
For example d/ < 0.1 means that the length of the confidence interval should not
be larger than two tenth of the population mean.
d/ < 0.1 and so 2d/ < 0.2
Example: The CVs of yield trials in our experimental station are never higher than
15%. How many replications are necessary to have a 95% CI for the true mean of
less than 1/10 of the average yield?
2d= 0.1
so
d= 0.1/2= 0.05
n= 1.962 0.152/0.052 = 34.6  35
8
2. 4. 3 Sample size for the estimation of the mean
Unknown 2. Stein's Two-Stage Sample
Consider a (1 - )% confidence interval about some mean µ:
Y-
t
2
s    Y + t  sY
, n 1
, n 1 Y
2
The half-length (d) of this confidence interval is therefore:
d  t
2
,n 1
sY  t 
2
,n 1
s
n
This formula can be rearranged to estimate necessary sample size n
2
s2
2 
n  t
 Z 2
2
,n1 d
d
2
2
2
Stein's Two-Stage procedure involves using a pilot study to estimate s 2.
Note that n is now present at both sides of the equation: iterative approach
Example: An experimenter wants to estimate the mean height of certain plants. From a
pilot study of 5 plants, he finds that s = 10 cm. What is the required sample size, if he
wants to have the total length of a 95% CI about the mean be no longer than 5 cm?
Using n = t2 /2,n-1 s2 / d2, n is estimated iteratively,
initial-n
5
123
62
64
t5%, df
2.776
1.96
2.00
2.00
n
(2.776)2 (10)2 /2.52 = 123
(1.96)2 (10)2 / 2.52 = 62
64
64
Thus with 64 observations, he could estimate the true mean with a CI no
longer than 5 cm at =0.05.
To accelerate the iteration you can start with Z:
n = z2 s2 / d2 = (1.96)2 (10)2 / 2.52 = 62
9
2. 4. 4 Sample size estimation for a comparison of two means
When testing the hypothesis Ho: o, we can take into account the possibility of
a Type I and Type II error simultaneously.
To calculate n we need to known the alternative 1 or at least the minimum
difference we wish to detect between the means  = |o - 1
The formula for computing n, the number of observations on each treatment, is:
n = 2 ( / (Z/2 + Z)
2
For = 0.05 and = 0.20, z= 0.8416 and z /2 = 1.96, (Z/2 + Z)2=7.85 8
We can define in terms of 


If δ = 2σ, n ≈ 4
If δ = 1σ, n ≈ 16

If δ = 0.5σ, n ≈ 64
We rarely know 2 and must estimate it via sample variances:
s

n  2 pooled 
  
2


 t


t
 ,n1n 22  ,n1n 22 
 2

2
, where
s pooled 
s12  s22
2
n is estimated iteratively. If no estimate of s is available, the equation may be
expressed in terms of the CV, and  as a proportion of the mean:
n  2 [(/) / ((Z/2 + Z)2  2(CV/%)2(Z/2 + Z)2
2
Example: Two varieties are compared for yield, with a previously estimated s =
2.25 (s=1.5). How many replications are needed to detect a difference of 1.5
tons/acre with a  = 5%, and  = 20%?
Approximate: n  2 (/(Z/2 + Z) = 2 (1.5/1.5)2(1.96+0.8416)= 15.7
2
Then use n = 2 (s / (t/2 + t) to estimate the sample size iteratively.
2
guesstimate n df = 2(n - 1)
16
30
17
32
t0.025
2.0423
2.0369
t0.20
0.8538
0.8530
estimated n
16.8
16.7
The answer is that there should be 17 replications of each variety.
10
2. 4. 5. Sample size to estimate population standard deviation
The chi-squared (2) distribution is used to establish confidence intervals around
the sample variance as a way of estimating the true, unknown population variance.
2. 4. 5. 1. The Chi- square distribution (ST&D p. 55)
0.5
2 df
4 df
6 df
0.4
0.3
0.2
0.1
0.0
1
2
2
3
4
5
6
Chi- sq uar e
Distribution of 2 , for 2, 4, and 6 degrees of freedom.
Relation between the normal and chi-square distributions.
The 2 distribution with df = n is defined as the sum of squares of n independent,
normally distributed variables with zero means and unit variances.
2α, df=1= Z2(0,1) α/2 2α/2, df=
2

1, 0.05 =
3.84 and Z2(0,1), 0.025 = t2, 0.025 = 1.962 = 3.84
Note: Z values from both tails go into the upper tail of the χ2 because of the disappearance of the minus sign in the
squaring. For this reason we use  for the 2 and /2 for Z and t.
n
Z  
2
i
i 1
(Yi   ) 2

2

1

2
 (Y  )
2
i
If we estimate the parametric mean  with a sample mean, we obtain:
1

2
 (Yi  Y ) 
2
(n  1) s 2

2
n
…due to: s 2  
i 1
(Yi  Y ) 2

n 1
n
 (Y  Y )
i 1
i
2
 (n  1) s 2
This expression, which has a 2n-1 distribution, provides a relationship between the
sample variance and the parametric variance.
11
2. 4. 5. 2. Confidence interval for 2
We can make the following statement about the ratio (n-1) s2/2 that has2n-1
distribution,
P { 21-/2, n-1  (n-1) s2/2  2/2, n-1} = 1 - 
Simple algebraic manipulation of the quantities in the inequality yields
P { 21-/2, n-1 /(n-1)  s2/2  2/2, n-1/(n-1)} = 1 - 
which is useful when the precision of s2 can be expressed in terms of the % of 2.
Or inverting the ratio and moving (n-1):
P {(n-1) s2/ 2/2, n-1  2  (n-1) s2/ 21-/2, n-1} = 1 - 
2
which is useful to construct 95% confidence intervals for  .
Example: What sample size is required to obtain an estimate of  that
deviates no more than 20% from the true value of  with 90% confidence?
2
2
Pr {0.8 < s/ < 1.2} = 0.90 = Pr {0.64 < s / < 1.44} = 0.90
thus
2

(1 - /2, n-1) / (n-1)=
2
0.64 and 
(/2, n-1) / (n-1)=
1.44
2
Since  is not symmetrical, the above two solutions may not identical for
small n. The computation involves an arbitrary initial n and an iterative
process:
n
21
31
41
36
35
df
(n-1)
20
30
40
35
35
1 - /2 = 95%
2
 (n-1)
 (n-1) /(n-1)
10.90
0.545
18.50
0.616
26.50
0.662
22.46
0.642
21.66
0.637
2
/2 = 5%
2
 (n-1)
 (n-1) /(n-1)
31.4
1.57
43.8
1.46
55.8
1.40
49.8
1.42
48.6
1.43
2
Thus a rough estimate of the required sample size is ~ 36.
12