Download Worksheet #5 on Quadratics

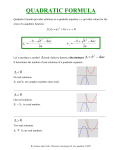
Algebra 2
Name: _____________________________
Quadratics: Worksheet Quad5
Period: _____
A quadratic equation is an equation that can be written in the form ax 2  bx  c  0 where a, b and c
are numbers. Some quadratic equations can be solved by factoring and using the fact that if the
product of two numbers is 0, then one of the numbers must be 0:
EXAMPLE 1:
Solve: 2 x 2  x  6
SOLUTION:
First subtract x and 6 from both sides to get an expression = 0:
2x 2  x  6  0
Then use FOIL to factor: (2 x  3)( x  2)  0
Since the product of the two numbers, (2x + 3) and (x – 2), is 0 one of them must be
0, so set 2x + 3 = 0 and x – 2 = 0 and solve these: x  
3
or x = 2
2
Not all quadratic trinomials can be factored, and you might be uncomfortable with factoring anyway.
A sure method for finding the solutions (also called “roots”) of a quadratic equation is to use the
quadratic formula:
QUADRATIC FORMULA:
If ax 2  bx  c  0 then x 
 b  b 2  4ac
2a
EXAMPLE 2:
Solve: 5 x 2  6 x  8  0
SOLUTION:
In this equation, a = 5, b = 6, and c = –8, so plug these values in the formula:
 6  6 2  4(5)( 8)  6  36  20(8)  6  36  (160)
x



2(5)
10
10
 6  36  160  6  196  6  14


10
10
10
There are two solutions: x 
 6  14 8 4
 6  14  20

 and x 

 2
10
10 5
10
10
EXAMPLE 3:
Solve: x( x  2)  2
SOLUTION:
First expand the left side, then subtract 2 from both sides to get x 2  2 x  2  0 .
This is the same as 1x 2  2 x  2  0, so a = 1, b = –2, and c = –2. Plug these values
in the quadratic formula:
Page 1 of 6
 (2)  (2) 2  4(1)( 2) 2  4  (8) 2  4  8 2  12
x



2(1)
2
2
2
Simplify 12 and write as two fractions:
x
22 3 2 2 3
 
 1 3
2
2
2
So the two solutions are x  1 3 and x  1 3 .
Sometimes you have to simplify an expression in an equation using FOIL. This is a method for
simplifying the product of binomials. In reverse, it is also a method for factoring a quadratic
expression.
EXAMPLE 4:
Use FOIL to simplify (3x  5)( 2 x  3)
SOLUTION:
FOIL stands for First, Outer, Inner, Last. These refer to products of the terms in each
binomial:
 15
6x 2
(3x + – 5)(2x
+ 3) = 6 x 2  9 x  10 x  15

6 x 2  x  15
 10x
9x
EXERCISES:
Problems 1-12: Solve the quadratic equation using factoring or the quadratic formula. Give answers
in simplified, exact form.
1.
x 2  6x  3  0
2.
Page 2 of 6
8 x 2  10 x  3
3.
x(2 x  1)  3
4.
x 2  2x  1
5.
9 x 2  17  6 x
6.
25 x 2  18 x  12 x  9
7.
x 2  3x  2
8.
x 2  4x  5
9.
2x 2  x  2  0
10.
x( x  2)  2
( x  6) 2  2
12.
( x  2) 2  4
11.
Page 3 of 6
13.
A “golden rectangle” is a rectangle which, when partitioned into a square and another rectangle,
results in the new rectangle having the same shape as the original rectangle. That is, in the figure
AB BC

below rectangle ABCD is a golden rectangle if rectangle BCFE is similar to it, so
.
BC CF
A
D
E
F
B
C
Some authors make a big deal about this and claim that such a rectangle is the “most pleasing” to
the eye. In fact, Dan Brown in The Da Vinci Code claims that golden rectangles and the related
ratio (symbolized by the Greek letter Φ, “Phi”) occur all over the place, including most of
Leonard da Vinci’s paintings. This, of course, is a lot of hooey. (See, for example, Martin
Gardner’s book, Fads and Fallacies in the Name of Science, Dover, 1957).
Find the exact value and an approximate value (to 3 decimal places) of Φ.
(Hint: Let BC = 1 unit. Then AB is Φ. Maybe you would prefer to call it x.)
Page 4 of 6
B
14.
Find AB:
x
A
C
2 5
2
x x2
F
15.
G
Find FG:
8
J
I
2
x  3 x  12
K
H
__________________________________________________________________________________
The number under the square root of the quadratic formula determines the types of roots you get when
a, b and c are real numbers. If that number is negative, then the roots contain the imaginary number i
and are complex conjugates. If that number is 0, then there is only one root and it is a real number,
and if positive there are two real roots.
So the magic number that determines the nature of the roots is b 2  4ac . Since this is an important
concept, it is given a special name: it is called the discriminant. That is,
The discriminant of the quadratic expression ax 2  bx  c is b 2  4ac .
Notice that the discriminant does NOT contain the square root. It is simply the stuff inside the square
root. Graphically, if the curve y  ax 2  bx  c does not intersect the x-axis then the discriminant
must be negative, if the graph is tangent to the x-axis then the discriminant is 0, and if it intersects the
x-axis twice then the discriminant is positive.
Page 5 of 6
More Exercises:
16.
If k is a real number and the equation x 2  6 x  k  0 has no real roots, then what must the be
the value of k?
17.
If k is a real number and the equation x 2  6 x  k  0 has only one real root, then what must the
be the value of k?
18.
If k is a real number and the equation kx 2  10 x  6  0 has two real roots, then what must the
be the value of k?
19.
If k is a real number and the equation 3x 2  kx  k  0 has only one real root, then what must
the be the value of k?
20.
If k is a positive real number and the graph of y  kx2  8 x  1
y
does not intersect the x-axis, then what must be the value of k?
O
Page 6 of 6
x