* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Lecture 6
Ceramic engineering wikipedia , lookup
Click chemistry wikipedia , lookup
Stoichiometry wikipedia , lookup
Electrochemistry wikipedia , lookup
Chemical reaction wikipedia , lookup
Colloidal crystal wikipedia , lookup
Determination of equilibrium constants wikipedia , lookup
Thermomechanical analysis wikipedia , lookup
Liquid–liquid extraction wikipedia , lookup
Internal energy wikipedia , lookup
Spinodal decomposition wikipedia , lookup
Marcus theory wikipedia , lookup
George S. Hammond wikipedia , lookup
Phase transition wikipedia , lookup
Geochemistry wikipedia , lookup
Bioorthogonal chemistry wikipedia , lookup
Thermodynamics wikipedia , lookup
Chemical equilibrium wikipedia , lookup
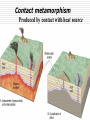
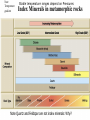
Lecture 6 Crystal Chemistry Part 5: Rock Suites Applications of Thermodynamics MARBLE DEMO Rock Cart, Kyanite. Andalusite, Sillimanite Serpentinite, Greenschist, Amphibolite Mica Schist with Staurolite, Microcline with Perthitic Texture Basaltic Magma Cooling - Bowen’s Reaction Series Molten- VERY Hot No solids First mineral to crystallize out Molten- Not so hot 100% Solid Fine crystals Need a microscope Fractionation minerals Low silica, HOT, fluid Course crystals Easily seen Intermediate High silica, warm, viscous Crystals can react with the melt if they touch it If the first formed crystals of Calcium-rich (Ca) Plagioclase touch the melt they will react with it, and will become more sodium-rich on their outer rims Zoned feldspar (plagioclase) showing change in composition with time in magma chamber (calcium-rich in core to sodium-rich at rim) FRACTIONATION: if early crystals are removed, the melt becomes richer in Silica Remove Fe, Mg, Ca Some Si Left with K and Al Most of Si You can start with a Mafic (silica-poor) magma and end up with some Felsic (silica-rich) Granites. Marble Demo A melt will crystallize its mafic components first, and the remaining melt may be granitic Assimilation and magmatic differentiation Show Samples Metamorphism 0 km Sedimentary rock Metamorphic rock Igneous rock Sediment Increasing depth and temperature 10 km ~200ºC 50 km ~800ºC Sedimentary rock The rocks don’t melt Metamorphism Melting Most metamor -phism occurs between about 200 and 800o C Contact metamorphism Produced by contact with heat source Hydrothermal Metamorphism Basaltic Magma MORs,Black Smokers, Cyprus & Bronze Age (Cu), Rome’s conquest of Britain (Sn), Sterling Zinc (and Manganese) Copper plus Tin makes Bronze Iron plus Carbon makes steel. http://collections.ic.gc.ca/geoscience/images/detail/F92S0220.jpg Circulation of hot water in cracks at mid-ocean ridge dissolves metals (Copper, Tin, Iron, Zinc, Lead, Barium) which are re-precipitated as sulfide ores. Hydrothermal waters are capable of metamorphism. Dynamothermal Metamorphism, Before collision Sediments are “unconsolidated”. They will fold if pushed. Dynamothermal Metamorphism, convergent margins (subduction, collision) in Note Temperature gradient Stable temperature ranges depend on Pressures Index Minerals in metamorphic rocks Note Quartz and Feldspar are not index minerals: Why? Thermometers and Pressure Gauges Polymorphs of Al2SiO5 Al2SiO5 solid - solid Sillimanite Kyanite Kyanite in Andalucite Andalusite Role of Volatiles - (H2O & CO2) Catalyzes reactions Mobility during metamorphism leads to non-isochemical reactions Dehydration and decarbonation during prograde reactions Lack of volatiles slows retrograde reactions Example: Dehydration: Muscovite + Qtz = K-spar + Sill. + H2O Metamorphic Facies near Subduction Zones and Arcs More Basaltic Magma formed by dehydration of ocean lithosphere and hydration of mantle We can note mineral facies in Metamorphic Rocks and determine where they formed. Greenschist Hand Sample Greenschist Thin Section Chl-Ep Blueschist glaucophane a sodic amphibole Amphibolite hornblende + Plag. Pleochroism, cleavage in hornblende Mineral Stability/Equilibrium Phase Stability The stability of a phase is determined by the Gibbs free energy, G. A Mineral of constant composition is considered a solid phase Mineral stability is commonly portrayed on a Phase Diagram Stability and Gibbs Free Energy G G(p,T) = E + PV − TS For a reaction or change of phase: System in equilibrium if no unbalanced forces DG = 0. If DG<0, a phase can spontaneously transform to another phase; e.g., solid to liquid If DG > 0, a phase transformation will not occur. Multiple phases can occur simultaneously. E + PV is Enthalpy H A certain amount of energy goes to an increase in entropy of a system and a certain amount goes to a heat exchange for a reaction. G = H –TS or DG0R = DH0R – TDS0R Gibbs Free Energy (G) is measured in KJ/mol or Kcal/mol DG ni G ( products) ni G (reactants ) 0 R 0 i i 0 i i G is a measure of driving force DGR = DHR – TDSR Again: For a reaction A B That is, for reactants products When DGR is negative the forward reaction has excess energy and will occur spontaneously A B When DGR is positive there is not enough energy in the forward direction, and the back reaction will occur B A When DGR is zero reaction is at equilibrium, both reactions occur equally. Petrology Field Trip to Bemco Mining District Supergene Enrichment, Bemco Mine Oxidation of Ferrous Iron, Fe+2 Groundwater: iron in two oxidation states Reduced soluble ferrous iron (Fe+2) Oxidized insoluble ferric iron (Fe+3). Modern atmosphere 21% oxygen, so most in shallow soils ferric state, (Fe+3). Initially Ferric hydroxide (Fe(OH)3) With time, mineralized. Decreasing solubility amorphous hydrous ferric oxide (Fe2O3•xH2O), Hematite (Fe2O3), and Goethite FeO(OH). Gibbs Free Energy Example Oxidation of ferrous ion to ferric ion DG0R = DH0R – TDS0R DGR0 ni Gi0 ( products) ni Gi0 (reactants ) i i H2O(l)=-63.32 kcal/mol = -63320 cal/mol (You look these up in these tables) Fe2+ + ¼ O2 + H+ Fe3+ + ½ H2O =[-4120+(-63320*0.5)]-[21870+(3954*0.25)] =[-67440]-[-20887.5]=-46557.5 cal/mol Negative, so forward (left to right) reaction will proceed Andalusite Al2SiO5 polymorphs differ in coordination of the Al+3 In Andalusite, one Aluminum is in 5-fold coordination, very unusual. http://www.uwgb.edu/DutchS/PETROLGY/coordinationx.htm Stability of a phase (or mineral) is partly related to its internal energy (here “E”), which strives to be as low as possible under the external conditions. Metastability exists in a phase when its energy is higher than P-T conditions indicate it should be. (1) Activation Energy is the energy necessary to push a phase from its metastable state to its stable state. (2 minus 1) Equilibrium exists when the phase is at its lowest energy level for the current P-T conditions. (3) (Two minerals that are reactive with one another, may be found to be in equilibrium at particular P-T conditions which on phase diagrams are recognized as phase boundaries) Note: most metamorphic and igneous minerals at the earth’s surface are metastable. Example: Exsolution of K-spar and Albite at low temperatures; they were in Solid Solution at higher temperatures. Components and Phases Components are the chemical entities necessary to define all the potential phases in a system of interest Here one Component, Al2SiO5 Phases: number of mineral species plus fluids Here three Phases: Ky, Sill, Andalucite And Degrees of Freedom f by Examples p+f=c+2 If T and P can change without changing the mineral assemblage, the system has two degrees of freedom f = 2 If neither T or P can change without changing the mineral assemblage, the system has zero degrees of freedom f = 0 If T and P must change together to maintain the same mineral, the system has one degree of freedom f=1 On a phase diagram f=0 corresponds to a point, f = 1 to a reaction line, f = 2 to a 1 phase area. Sill. Ky. And. The Phase Rule The number of minerals (phases) that may stably coexist is limited by the number of chemical components p+f=c+2 where P is the number of mineral phases, c the number of chemical components, and f is the number of degrees of freedom. Basic Thermodynamics The theoretical basis of phase equilibrium Three Laws of Thermodynamics 1. First Law: Change in Internal Energy (E)= dE = dQ – dW Q – heat energy W – work = F * distance (notice distance is a length) Pressure has units Force/Area = (F/dist2) so F* dist = P * area * dist = P * V At constant pressure dW = PdV So if Pressure is constant: (1) dE = dQ – PdV where dV is thermal expansion or contraction Second and Third Laws of Thermodynamics 2. All substances move to the greatest state of disorder (highest Entropy ”S”) for a particular T and P. (2) dQ/T = dS “The state of greatest order [lowest S] is at the lowest temperature. With increasing temperature, disorder becomes more prevalent.” Minerals with simple atomic structure and simple chemistry have lower entropy. 3. At absolute zero (0ºK), Entropy is zero Does this suggest how to measure S? Can we measure changes in S by keeping track of temperature as we add heat to a system? “The entropy of a pure crystalline substance can therefore be obtained directly from heatcapacity measurements by assuming that S0 (at 0o K) is zero” Wood and Fraser (1978) p38 ss Gibbs Free Energy Define G – the energy of a system in excess of its internal energy E. This is the energy necessary for a reaction to proceed G = E + PV – TS Differentiating dG = dE +PdV +VdP -TdS - SdT dE = dQ - PdV = TdS – PdV so dG = TdS – PdV + PdV + VdP -TdS – SdT = VdP –SdT This is equation (3) dG = VdP –SdT If T = constant dT = 0, then dG = VdP, if V decreases, P can increase without increasing G (2) at constant T (dG/dP)T = V (dense (low V) phases are favored at high P) If P = constant dP = 0, then dG = -SdT, if T increases then S can increase without increasing G (3) at constant P (dG/dT)P = -S (disordered phases (high S) are favored at high T) Enthalpy Earlier we saw G(T,p) = E + pV − TS • But the Enthalpy H(S,p) = E + pV • So DG = DH –TDS DH can be measured in the laboratory with a calorimeter. DS can also be measured with heat capacity measurements. Values are tabulated in books. Clapeyron Equation • Defines the state of equilibrium between reactants and products in terms of S and V From Eqn.3, if dG =0, dP/dT = ΔS / ΔV (eqn.4) The slope of the equilibrium curve will be positive if S and V both decrease or increase with increased T and P The function G can be represented graphically on P T diagrams Constructing Phase Diagrams One Component: H2O Pressure-Temperature Phase Diagram The Gibbs and Clapeyron Equations allow us to estimate phase diagrams with extrapolations from laboratory measurements. The lines show where equilibrium conditions (DG = 0) occur. Clapeyron tells us the slope The Payoff • Our experiments and calculations allow us to construct the 3-D plot in (a), and to project the mineral with the lowest free energy at each PT onto the graph in (b). Notice the points a,b and c at right. At c, DG = 0 in the reaction Andalucite Sillimanite Nesse fig 5.3 The KSA Phase diagram allows us to assign PT conditions to various Plate Tectonic settings Of Nesse