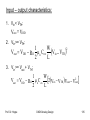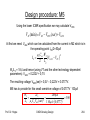* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download CMOS Analog Design Lecture Notes Rev 1.5L_02_06_11
Oscilloscope types wikipedia , lookup
Coupon-eligible converter box wikipedia , lookup
Schmitt trigger wikipedia , lookup
Power electronics wikipedia , lookup
Electronic engineering wikipedia , lookup
Valve RF amplifier wikipedia , lookup
Analog television wikipedia , lookup
Radio transmitter design wikipedia , lookup
Switched-mode power supply wikipedia , lookup
Broadcast television systems wikipedia , lookup
Analog-to-digital converter wikipedia , lookup
Integrated circuit wikipedia , lookup
Power MOSFET wikipedia , lookup
Operational amplifier wikipedia , lookup
Transistor–transistor logic wikipedia , lookup
Telecommunication wikipedia , lookup
Resistive opto-isolator wikipedia , lookup
Current mirror wikipedia , lookup
Rectiverter wikipedia , lookup
CMOS Analog Design
LECTURE NOTES
Prof. Dr. Bernhard Hoppe
Introduction
Prof. Dr. Hoppe
CMOS Analog Design
2
Analog Integrated Circuits Design Steps:
1.
2.
3.
4.
5.
6.
7.
Definition
Implementation
Simulation
Geometrical description
Simulation including the geometrical parasitics
Fabrication
Testing and verification
Prof. Dr. Hoppe
CMOS Analog Design
3
Analog Integrated Circuits Design:
Tools & Methods:
•
•
•
Simulation
Design Capture
Hand Calculations
Prof. Dr. Hoppe
Bottom – Up
Flow
CMOS Analog Design
4
Discrete Analog Circuit Design
- Using breadboards
Integrated Analog Circuit Design
- Using computer simulation techniques
Prof. Dr. Hoppe
CMOS Analog Design
5
Pros and Cons of Computer simulations
Advantages:
1.
2.
3.
4.
5.
No breadboards required
Every node in the circuit is accessible
Feedback loops may be opened
Modification of the circuit is easy
Modification of processes and ambient conditions is
possible
Prof. Dr. Hoppe
CMOS Analog Design
6
Pros and Cons of Computer simulations
Drawbacks:
1. Accuracy of models
2. Convergence problems of the simulator: circuit may
not converge to a stable operating point
3. Time required to perform simulations of large circuits
4. Use of the computer as a substitute for thinking
Prof. Dr. Hoppe
CMOS Analog Design
7
The PN junction
Prof. Dr. Hoppe
CMOS Analog Design
8
PN junction
Used for:
1. Insulation purposes
2. Diodes and zeners
3. Basic structure of MOS and Bipolar transistor
Prof. Dr. Hoppe
CMOS Analog Design
9
Important features for device properties
And modelling aspects
•
•
•
•
Depletion region width
Depletion region capacitance
Reverse bias breakdown voltage
Diode equation iD Vs VD
Prof. Dr. Hoppe
CMOS Analog Design
10
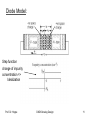
Diode Model:
Step function
change of impurity
concentration =>
Idealization
Prof. Dr. Hoppe
CMOS Analog Design
11
Diode Model:
Space charge
width
Xd = Xn - Xp
Equilibrium
condition:
Field forces =
Diffusion forces
Prof. Dr. Hoppe
CMOS Analog Design
12
Xd = ?, E0 = ?, Φ0 = ?
Due to electrical neutrality, the charge on either side of
the junction must be equal
Thus,
qNDXn = qNAXp
where q = 1.6 x 10-19 C
To calculate the fieldstrength from the charge,
Gauss equation:
dE(x) = qN
dx
εSi
where εSi = 11.7x8.85x10-14 F/cm – Si dielectric constant
Prof. Dr. Hoppe
CMOS Analog Design
13
On integration we get the max electric field at the
junction, E0
E0 = 0
∫
Therefore,
Prof. Dr. Hoppe
E0
dE = Xp
∫
0
E0 =
–qNA / εSi dx
-qNDXn
εSi
CMOS Analog Design
=
qNAXp
εSi
14
Voltage is found by integrating the electric field, resulting
in
Φ0 - VD
-E0(Xn – Xp)
=
2
where VD = applied external voltage
Φ0 = barrier potential
Prof. Dr. Hoppe
CMOS Analog Design
15
Barrier potential Φ0 is given as
Φ0 = (kT / q) ln (NAND / ni2) = (Vt) ln (NAND / ni2)
where k = Boltzmann‘s constant 1.38 x 10-23 J/K
ni = intrinsic concentration of silicon
1.45 x 1010 /cm3 at 300K
Vt = 25.9 mV at 300K
Prof. Dr. Hoppe
CMOS Analog Design
16
Using equations for E0 and Φ0 – VD, and solving for Xn
or Xp we get
Xn =
and
Prof. Dr. Hoppe
(
Xp = -
2εSi(Φ0 – VD)NA
qND(NA + ND)
(
)
2εSi(Φ0 – VD)ND
qNA(NA + ND)
CMOS Analog Design
1/2
)
1/2
17
Width of the depletion region Xd is given as
Xd = Xn – Xp =
Prof. Dr. Hoppe
(
2εSi(NA + ND)
qNAND
CMOS Analog Design
)
1/2
(Φ0 - VD)1/2
18
Conclusions:
1.
2.
3.
4.
Xd is proportional to (Φ0 - VD)1/2 or (- VD)1/2
If NA >> ND then Xd ~ Xn
If ND >> NA then Xd ~ Xp
Lower doped side determines Xd
Prof. Dr. Hoppe
CMOS Analog Design
19
Depletion charge and depletion layer
capacitance:
Depletion charge Qj is given as
Qj = |AqNAXp| = AqNDXn
(
Qj = A
2εSiqNAND
(NA+ND)
)
1/2
(Φ0 - VD)1/2
where A is the cross sectional area of the pn junction
Prof. Dr. Hoppe
CMOS Analog Design
20
Depletion charge and depletion layer
capacitance:
Magnitude of the electric field at the junction
E0
=
2qNAND
( ε (N +N ) )
Si
Prof. Dr. Hoppe
A
1/2
(Φ0 - VD)1/2
D
CMOS Analog Design
21
Depletion charge and depletion layer
capacitance:
Depletion layer capacitance Cj is given as
dQj
Cj = dV = A
D
(
=
Prof. Dr. Hoppe
εSiqNAND 1/2
-1/2
(Φ
V
)
0
D
2(NA+ND)
)
Cj0
[1-(VD /Φ0)]m
CMOS Analog Design
22
Depletion charge and depletion layer
capacitance:
where Cj0 is capacitance when VD = 0
m is a grading coefficient
m = 1/2 => step junction
m = 1/3 => linearly graded junction
1/3 <= m <= 1/2 => real junctions
(experimental fit)
Prof. Dr. Hoppe
CMOS Analog Design
23
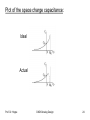
Plot of the space charge capacitance:
Ideal
Actual
Prof. Dr. Hoppe
CMOS Analog Design
24
Example:
Calculate Xd, Xn ,Xp, E0, Cj0, and Cj
for VD = -4 V,
NA = 5 x 1015 /cm3,
ND = 1020 /cm3,
A = 10 μm x 10 μm
Temperature = 300 K
Results: 0=0.917V
Cj(-4V) = 9.18fF
Prof. Dr. Hoppe
xn 0 xp= 1.128µm Cj0 = 20.3fF
CMOS Analog Design
25
Breakdown voltage of a reverse biased diode:
BV =
(
εSi(NA + ND)
2qNAND
)(E
2
)
max
assuming |VD > Φ0|
Emax is the maximum electric field that can exist
across the depletion region
For silicon, Emax ~ 3 x 105 V/cm
Prof. Dr. Hoppe
CMOS Analog Design
26
Breakdown mechanisms:
1. Avalanche breakdown: Multiplication of carrier
concentrations due to collisions of minority carriers
with the electrons of the atoms in the lattice. It has a
negative temperature coefficient.
2. Zener breakdown: Valence band breakdown. It
occurs at comparatively lower voltages. It does not
depend upon temperature (tunneling effect).
Prof. Dr. Hoppe
CMOS Analog Design
27
Breakdown mechanisms:
Reverse biased current (due to avalanche effect)
iRA = MiR =
([1- (V
1
n]
/BV)
R
) xi
R
where M = avalanche multiplication factor
n = empirical parameter 3 <= n <= 6
iR = ‘normal‘ reverse current
Prof. Dr. Hoppe
CMOS Analog Design
28
Typical pn junction characteristics:
Prof. Dr. Hoppe
CMOS Analog Design
29
Voltage-Current relationship of diode:
Impurity concentration profile for diffused pn junction
under forward bias: Minorities pile up at the boundaries of
the depletion region!
Prof. Dr. Hoppe
CMOS Analog Design
30
Voltage-Current relationship of diode:
Minority carrier concentration for diffused pn
junction:
no applied voltage: no excess minority carrier
concentration: np(0) = np0 and pn(0) =pn0
Reverse biased (vD negative): minority carrier
concentration is depleted below the equilibrium
value!
Current in reverse biased pn-junction is a diffusion
current, depending on the slope of the minority
carrier concentration at the boundaries of the
depletion region.
Prof. Dr. Hoppe
CMOS Analog Design
31
Voltage-Current relationship of diode:
Terminologies:
pn0 and np0 = equilibrium concentrations of the minority
carriers in n-type and p-type regions
pn(0) = pn0 exp(VD/Vt) is value of the excess
concentration at x = 0
np(0) = np0 exp(VD/Vt) is value of the excess
concentration at x‘ = 0
Prof. Dr. Hoppe
CMOS Analog Design
32
Voltage-Current relationship of diode:
The total current in an pn junction diode is given as
iD = qA
(
Dppn0
Dnnp0
(exp(VD/Vt) – 1)
Lp + Ln
)
Or
iD = Is (exp(VD/Vt) – 1)
Prof. Dr. Hoppe
CMOS Analog Design
33
Voltage-Current relationship of diode:
where
Is = qA
(
Dppn0
Dnnp0
Lp + Ln
)
is a constant called the saturation current
A = area of the pn junction
Dp = diffusion constant of holes in n-type semiconductor
Dn = diffusion constant of electrons in p-type
semiconductor
Lp = diffusion length for holes in n-type semiconductor
Ln = diffusion length for el. in p-type semiconductor
Prof. Dr. Hoppe
CMOS Analog Design
34
Example:
Calculate the saturation current of a pn junction diode
with
NA = 5 x 1015 /cm3, ND = 1020 /cm3,
A = 1000 μm2 , Dn = 20 cm2 / s,
Dp = 10 cm2 / s, Ln = 10 μm,
Lp = 5 μm.
Prof. Dr. Hoppe
CMOS Analog Design
35
The MOS transistor
Prof. Dr. Hoppe
CMOS Analog Design
36
N-well technology:
Physical structure of an n-MOS and p-MOS device:
Prof. Dr. Hoppe
CMOS Analog Design
37
N-well technology:
•
•
•
•
•
•
pMOS formed within a lightly doped n- material
called the N-well
nMOS formed within a lightly doped p- substrate
Both types of transistors are four terminal devices
The p-bulk connection is common throughout the
integrated circuit and is connected to Vss (the most
negative supply)
Multiple n-wells can be connected to different
potentials (but +ve w.r.t. Vss)
nMOS and pMOS devices are complementary:
nMOS equations can be mapped to pMOS
equations
Prof. Dr. Hoppe
CMOS Analog Design
38
nMOS threshold voltage equation:
Cross section of an n-channel transistor with all
terminals grounded:
Prof. Dr. Hoppe
CMOS Analog Design
39
nMOS threshold voltage equation:
Terminologies:
Cox = Area specific oxide capacitance in F/m2
ΦF = Equilibrium electrostatic potential (Fermi potential) in
the semiconductor
ΦS = Surface potential of the semiconductor
ΦMS = Difference in the work functions between the gate
material and bulk silicon in the channel region
QSS = Undesired +ve charge present in the interface
between the oxide and the bulk silicon
Qb0 = Fixed charge in the depletion region
VSB = Substrate bias (VSource - VSubstrate)
Prof. Dr. Hoppe
CMOS Analog Design
40
nMOS threshold voltage equation:
Threshold voltage VT consists of following contributions:
1. ΦMS = ΦF (substrate) - ΦF (gate)
where ΦF (metal) = 0.6 V
2. [-2ΦF – (Qb /Cox)]: voltage required to change the
surface potential and offset the depletion layer charge
3. Undesired +ve charge QSS due to impurities and
imperfections at the interface – must be compensated
by a gate voltage of – QSS /Cox
Prof. Dr. Hoppe
CMOS Analog Design
41
nMOS threshold voltage equation:
Summation of the contributions:
VT = ΦMS + [-2ΦF – (Qb /Cox )] + (– QSS /Cox )
= ΦMS - 2ΦF – (Qb0 /Cox ) – (QSS /Cox ) - (Qb - Qb0 ) / Cox
The threshold voltage can be rewritten as
VT VT 0
2F VSB 2F
where VT0 = ΦMS - 2ΦF – (Qb0 /Cox ) – (QSS /Cox )
Prof. Dr. Hoppe
CMOS Analog Design
42
Body effect coefficient:
The body factor, body effect coefficient, or bulk-threshold
parameter γ is defined as
γ=
Prof. Dr. Hoppe
√2qεSiNA
Cox
CMOS Analog Design
(unit: V1/2)
43
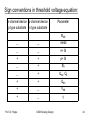
Sign conventions in threshold voltage equation:
n-channel device p-channel device
p type substrate n type substrate
Parameter
ΦMS
_
_
metal
_
_
n+ Si
+
+
p+ Si
_
+
ΦF
_
+
Qb0, Qb
+
+
QSS
+
_
VSB
+
_
γ
Prof. Dr. Hoppe
CMOS Analog Design
44
Example:
Calculate the threshold voltage and body factor γ for an
n-channel transistor with an n+-silicon gate for no
substrate bias and a Vsb od 2V if
tox = 200 Angström ,
NA = 3 x 1016 /cm3,
gate doping ND = 4 x 1019 /cm3,
surface charge density NSS = 1010 /cm2,
temperature = 300 K.
Prof. Dr. Hoppe
CMOS Analog Design
45
Solution (1):
tox = 200 Angström,
NA = 3 x 1016 /cm3,
ND = 4 x 1019 /cm3,
NSS = 1010 /cm2,
Temperature of 300 K means
• kBT/q = 0.026V (Temperature Voltage)
• ni = 1.45 x 1010 /cm3 (Intrinsic Carrier Concentration)
Si 11,7 0
Prof. Dr. Hoppe
CMOS Analog Design
46
Solution (2):
Formula for the threshold-voltage:
VT VT 0
with the Fermi-potential:
ni
k BT
ln
q
NA
F
sub
The zero substrate bias threshold voltage is:
VT 0 MS
Qb0 QSS
2F
Cox Cox
2F VSB 2F
F gate
k BT N D
ln
q
ni
Pdoped
Ndoped
The space charge in the channel
Qb0 2q N A Si 2F
The work-function difference
MS F sub F gate
Prof. Dr. Hoppe
CMOS Analog Design
47
Solution (3):
The work-function difference and
MS F sub F gate 0.026V ln
1.45e 10
4.0e 19
0.026V ln
3e 16
1.45e 10
0.38V 0.57V 0.95V
the space charge induced potential in the channel
Qb 0 2q N A Si 2F
ox
Cox
tox
2 (1.6e 19) (3.0e 16) 11.7 (8.854e 14) 0.76 As / cm 2
3.9 (8.854e 14) /(200.0e 10)
As / Vcm 2
(8.7e 8) As / cm 2
0.51V
2
(170.0e 9) As / Vcm
Prof. Dr. Hoppe
CMOS Analog Design
48
Solution (4):
The body-factor reads
2q N A Si 2F
Cox
Qb 0
2F Cox
0.51
V 0.58 V
0.87
So the threshold voltage without substrate bias is
VT 0 0.95V 0.76V 0.51V 0.01V 0.33V
and for Vsb = 2V we get:
VT 0.33V 0.58( 0.76 2.0 0.76)V 0.78V
Prof. Dr. Hoppe
CMOS Analog Design
49
Current voltage relation of the MOS transistor:
1. Linear mode: - Sah equation
iD = (W/L)μnCox [(VGS – VT) – (VDS/2)] VDS
holds good for (VGS – VT) >= VDS and VGS >= VT
2. Saturation mode:
iD = (W/2L)μnCox [(VGS – VT)2]
holds good for (VGS – VT) <= VDS
Prof. Dr. Hoppe
CMOS Analog Design
50
Device transconductance parameter:
The factor μnCox is defined as the device
transconductance parameter, given as
K‘ = μnCox = μnεox / tox
Prof. Dr. Hoppe
CMOS Analog Design
51
CMOS device modeling
Prof. Dr. Hoppe
CMOS Analog Design
52
Pinch-off Saturation:
•
•
•
•
Voltage drop in the channel is constant
The Field pulling the electrons from the source
remains constant
iD remains constant
Electrons are injected from the channel into the
space charge region => ballistic transport to drain
node
Prof. Dr. Hoppe
CMOS Analog Design
53
How large is the saturation current ?:
Saturation condition:
VDS = (VGS – VT)
Saturation current equation:
iD = (W/2L)μnCox [(VGS – VT)2]
holds good for 0 <= (VGS – VT) <= VDS
Prof. Dr. Hoppe
CMOS Analog Design
54
Output characteristics of the MOSFET for
VT = 1V:
Prof. Dr. Hoppe
CMOS Analog Design
55
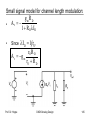
Channel length modulation effect:
•
•
•
•
Constant saturation current – only for long channel
devices i.e. Pinch-off point „close“ to the drain
Long channel devices have length L >= 10 μm
For lengths shorter than 1 μm, short channel effects
are observed
Most important effect: Channel length modulation
effect
Prof. Dr. Hoppe
CMOS Analog Design
56
Channel length modulation effect:
•
•
In reality, the saturation current depends linearly on
VDS
Modified current equation:
iD = (W/2L) μnCox [(VGS – VT)2 (1 + λVDS)]
where λ = channel length modulation factor (unit: 1/V)
Prof. Dr. Hoppe
CMOS Analog Design
57
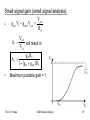
Kleinsignalparameter
•
•
Kleinsignalparameter beschreiben das Verhalten eines
Systems in der Nähe eines Arbeitspunktes
In Sättigung gilt für die Abhängigkeit des Drainstroms
von der Gate Source Spannung (Vds und Vsb fest)
I D
Vds fest
Eingangsleitwert g m
V gs
W
2 n Cox I D
L
W
gm nCox V GS V TH
L
g m f VGS VTH
2 ID
VGS VTH
A g m R D
spannungsabhängig
Nichtlinearität!
Prof. Dr. Hoppe
CMOS Analog Design
58
Kleinsignalparameter
•
In Sättigung gilt für die Abhängigkeit des Drainstroms
von der der Drain-Source-Spannung bei fester Gate
Source Spannung
Ausgangsleitwert
g ds
I D
Vgs fest
V ds
1
W
gds nCox V GS V TH ² I D
2
L
1/gds = ro der Ausgangswiderstand des Transistors
Prof. Dr. Hoppe
CMOS Analog Design
59
Kleinsignalparameter
•
In Sättigung gilt für die Abhängigkeit des Drainstroms
von der
der Source-Bulk-Spannung bei fester Drain-Source- und
Gate Source Spannung
Substratabhängigkeit
gmbs
g mbs
I D
Vgs & Vds fest
V SB
I D VT
I D
I D
g
gm
m
VBS VSB
2 2 F VSB
VT VSB
Ändert sich VSB, dann ändert sich die Einsatzspannung und damit der Strom im Transistor!
Prof. Dr. Hoppe
CMOS Analog Design
60
Kleinsignalparameter Leitwerte gm und gds
•
In Sättigung gilt für die Abhängigkeit des Drainstroms
von der der Drain-Source-Spannung bei fester Gate
Source Spannung
I D
Vgs fest
g ds
V ds
1
W
gds nCox V GS V TH ² I D
2
L
1/gds = ro der Ausgangswiderstand des Transistors
Prof. Dr. Hoppe
CMOS Analog Design
61
Transfer characteristics of the MOSFET:
iD plotted against VGS for fixed VDS, VT = 2V
Prof. Dr. Hoppe
CMOS Analog Design
62
Short channel effects:
•
•
•
As technology scaling reaches channel lengths
shorter than 1 μm, second order effects become
significant
MOSFETs with L < 1 μm are called short channel
devices
Main effects:
1. velocity saturation
2. threshold voltage variation
3. hot carrier effect
Prof. Dr. Hoppe
CMOS Analog Design
63
Review of classical derivation of iD:
Gradual Channel Approximation:
x-direction perpendicular to the surface,
y-direction from 0 to L: the channel
VT is assumed to be constant along the channel
Electrical field in y-direction much larger than the field in x-direction
Current flow in the channel in y-direction only
The whole channel is assumed to be inverted: VGS > VT VGD = VGS - VDS > VT
Prof. Dr. Hoppe
CMOS Analog Design
64
Review of classical derivation of iD:
The mobile charge in the channel flows along the y-direction driven by Ey
The mobile charge at position y depends on VGS and the channel voltage Vc(y) is
Q(y) = -Cox [VGS - Vc(y) - VT]
...(1)
Note:
The channel is tapered as we move from source to drain as the gate to channel voltage
causing surface inversion is smaller at the drain end!
Prof. Dr. Hoppe
CMOS Analog Design
65
Review of classical derivation of iD:
The incremental resistance of the segment dy reads:
dR
dy
W n Q( y )
……2
Current iD is flowing from source and drain in y-direction (1-dimensional model)
Voltage drop along dy:
iD dy
…….3
dV i dR
D
Prof. Dr. Hoppe
W n Q( y )
CMOS Analog Design
66
Review of classical derivation of iD:
Integration along y from 0 to L yields :
L
i
D
dy W n
0
VDS
Q( y )dV
C
0
We insert equ.1 for Qc(y) and obtain
iD L W Cox n
VDS
V
GS
Vc ( y ) VT dVc
0
Assuming that the Channel Voltage is the only voltage depending on y
we obtain for the current iD
iD
Prof. Dr. Hoppe
W
2
nCox 2 VGS VT VDS VDS
2L
CMOS Analog Design
67
Review of classical derivation of iD:
iD depends on µn and Cox = ox/tox : technology dependent
and on geometry W and L, channel width (W) and length (L)
W/L is the most important design parameter
W
2
iD
nCox 2 VGS VT VDS VDS
2L
Example: µn = 600cm2/Vs Cox= 7,0*10-8F/cm2 W=20µm L = 2µm VT=1.0V
2
iD 0, 21mA / V 2 2 VGS 1,0 VDS VDS
iD curves are inverted parabolas with maximum at VDS=VGS-VT
Beyond this voltage: negative differential transconductance
Not observed in real MOSFETs
Prof. Dr. Hoppe
CMOS Analog Design
68
Review of classical derivation of iD:
iD
W
2
nCox 2 VGS VT VDS VDS
2L
Dashed curves represent unphysical behaviour!
Prof. Dr. Hoppe
CMOS Analog Design
69
Review of classical derivation of iD:
iD-formula derived for complete channel is inverted
VGS VT
VGD VGS VDS VT
This is the linear operating region
not valid beyond the linear/saturation boundary:
VDS VGS VT VDSAT
Above VDSAT current increases no more
iD
W
2
nCox 2 VGS VT VDSAT VDSAT
2L
2
W
nCox VGS VT , saturation current
2L
Prof. Dr. Hoppe
CMOS Analog Design
70
Channel length modulation
If VDS > VDSAT the channel is no longer inverter at the drain end.
Surface potential is too low: Pinch off effect!
VDS VGS VT VDSAT
Above VDSAT the channel charge at the drain end becomes zero (very small)
Q(y=L) 0
Prof. Dr. Hoppe
CMOS Analog Design
71
Channel length modulation
Saturation effect = onset of pinch-off of channel at the drain end y = L
If VDS > VDSAT the pinch off at L‘ = L - L
Pinched off part of channel is depleted:
Q( y ) 0 für L ' y L
Vc ( y L ') VDSAT
Gradual channel approximation valid from y = 0 to y = L‘:
2
W
iD
nCox VGS VT
2L '
As L‘ reduces with increasing VDS further beyond VDSAT iD is growing in
saturation with drain-source-voltage
Prof. Dr. Hoppe
CMOS Analog Design
72
Channel length modulation
We may rewrite the saturation current
1 W
2
iD
C
V
V
L 2 L n ox GS T
1
L
L may be shown to be proportional to
L VDS VDSAT
There is the following empirical relationship
L
1
1 VDS with VDS 1
L
1 W
2
W
2
iD
n Cox VGS VT
n Cox VGS V 1 VDS
2L
1 L 2 L
L
Prof. Dr. Hoppe
CMOS Analog Design
73
Channel length modulation
Prof. Dr. Hoppe
CMOS Analog Design
74
Equivalent derivation of iD using gradual
channels:
iD = - vn(y)Q(y)W
...(2‘)
Current is charge at surface times width of the channel
moving with the electron velocity vn ~ E, therefore
vn = - μnE(y) = - μndV/dy
...(3‘)
Substituting eq.(1) and (3) in (2) we get
iDdy = μn CoxW [VGS - V(y) - VT] dV
Prof. Dr. Hoppe
CMOS Analog Design
...(4‘)
75
Review of classical derivation of iD:
Integrating eq.(4) along the channel for 0 to L gives
iD = (W/L)μnCox [(VGS – VT) – (VDS/2)] VDS
This derivation shows, that drain current is depending on
the carrier mobility, which was assumed to be
constant as in the case of the drift velocity in
conductors like copper.
However the velocity saturates at strong fields giving rise
to the velocity saturation effect in short channel
transistors and hence the mobility gets field
dependent!
Prof. Dr. Hoppe
CMOS Analog Design
76
Velocity saturation effect:
Measurements of vn as a function of E
•
•
The most important short-channel effect in
MOSFETs is the velocity saturation of carriers in the
channel.
A plot of electron drift velocity versus electric field is
shown above.
Prof. Dr. Hoppe
CMOS Analog Design
77
Impact of velocity saturation:
Velocity of electrons as a function of E:
vn =
μ nE
1 + E/Ec
vn = vsat
for E < Ec
for E >= Ec
where Ec is the critical electric field at which velocity
saturation occurs
Inserting a factor in the equation of iD, we get:
iD = K(VDS)(W/L)μnCox [(VGS – VT) – (VDS/2)] VDS
Prof. Dr. Hoppe
CMOS Analog Design
78
Impact of velocity saturation:
where
1
K(VDS) =
1 + VDS/EcL
is a SPICE parameter for modeling.
For L >> 1 μm, K(VDS) ~ 1
For short channel devices, K(VDS) < 1 resulting into
smaller iD than expected
Prof. Dr. Hoppe
CMOS Analog Design
79
Impact of velocity saturation:
How large is the current?
Assume that carrier velocity has reached limit value vn = 107 cm/s
The effective channel length Leff will be shorter than L:
Leff
iD ( sat ) W vn ( sat ) q n( x ) dx W vn ( sat ) Q
0
Since the voltage at Leff is VDSAT we have:
Leff
iD ( sat ) W vn ( sat ) q n( x ) dx W vn ( sat ) Cox VDSAT
0
Drain current is independent of channel length
Drain current is linear with drain-source-voltage
Prof. Dr. Hoppe
CMOS Analog Design
80
Impact of velocity saturation:
Short channel transistors enter the saturation region
before VDS = VGS – VT
iD ( sat ) W vn ( sat ) Cox VDSAT W µn VDSAT Cox VDSAT
VDSAT 2
W
iD ( sat ) K Cox µn VGS VT VDSAT
L
2
gleichsetzen und nach VDSAT auflösen
VDSAT
Prof. Dr. Hoppe
2
K VGS VT
3
CMOS Analog Design
81
Impact of velocity saturation (second impact):
For short channel devices, K(VGS – VT) < 1
Two transistors with same W/L and VGS = VDD will have
the following characteristics:
Prof. Dr. Hoppe
CMOS Analog Design
82
Velocity saturation (0,25µm CMOS)
W/L=25µm/2,5µm,
Imax = 5,4mA
W/L=2.5µm/0,25µm,
Imax = 2,2mA
W/L=10µm/1,0µm,
Imax = 4,3mA
Prof. Dr. Hoppe
CMOS Analog Design
83
A simple model for hand calculations:
(1) Velocity saturation occurs abruptly at E = Ec
vn = μnE
for E < Ec
vn = vsat = μnEc
for E >= Ec
(2) VDSsat at which Ec is reached is given as
VDSsat = LEc = Lvsat /μn
(3) Approximate saturation current for a short channel
device is given as
iDsat = vsat CoxW [VGS – VT – VDSsat]
Prof. Dr. Hoppe
CMOS Analog Design
84
iD Vs VGS characteristics for long and short channel
devices:
Two transistors, both with W/L = 1.5 will have
the following characteristics:
Prof. Dr. Hoppe
CMOS Analog Design
85
Threshold voltage variations in long and short
channel devices:
Long channel nMOS:
VT = f (technology, source – bulk voltage)
Short channel nMOS:
VT = f (technology, source – bulk voltage, L, W, VDS)
Prof. Dr. Hoppe
CMOS Analog Design
86
Disadvantages of short channel devices:
•
•
•
•
Reduction in gain
Cannot switch off properly due to reduction in VT
More leakage current in the „off“ condition
More dependence on transistor variables
Prof. Dr. Hoppe
CMOS Analog Design
87
Hot carrier effect:
•
•
•
•
•
•
During the last decade, transistor dimensions were
scaled down but not the power supply
Increase in the field strength causes increase in the
kinetic energy of electrons (hot electrons)
Some of the electrons become so ‘hot‘ that they can
jump over the barriers and tunnel into the oxide
Electrons are trapped in the oxide and these
additional charges increase VT of the transistors
This leads to a long term reliability problem
For an electron to become hot, a field strength
greater than 104 V/cm is needed, which is easily
possible for technologies with L < 1 µm
Prof. Dr. Hoppe
CMOS Analog Design
88
iD Vs VDS characteristics degradation:
Hot carrier effect degrades the V-I characteristics of
short channel transistors due to extensive usage or
aging problem
Prof. Dr. Hoppe
CMOS Analog Design
89
Process variations:
Device parameters vary between different wafer runs
and even on the same die!....why?
Answers :
(1) Variations of process parameters:
– impurity concentrations
– oxide thickness
– diffusion depths
(2) Temperature effects due to non uniform conditions:
– variations in sheet resistances
– variations in threshold voltages
– variations in parasitic capacitances
Prof. Dr. Hoppe
CMOS Analog Design
90
Process variations:
(3) Variations in geometry of the devices:
– limited resolution of the lithographic processes
results into variations in W/L ratios for the
neighbouring transistors
– device mismatch in circuits built on the basis of
transistor pairs, for ex: differential stages
Prof. Dr. Hoppe
CMOS Analog Design
91
Transistor typical parameter values:
0.25 µm technology, VDD = 2.5V, Minimum channel length
device
n-channel device p-channel device
Parameter
0.43
-0.40
VT0 (V)
0.4
-0.4
γ (V1/2)
0.65
-1.0
VDSsat (V)
115
-30
K‘ (μA/V2)
0.06
-0.1
λ (V-1)
0.7
0.8
2F
Prof. Dr. Hoppe
CMOS Analog Design
92
Basic Transistor Formulas:
iD 0
cutoff
linear
iD
VGS VT
W
2
nCox 2 VGS VT VDS VDS
2L
VGS VT VDSSAT
VGS VT VDSSAT
W
2
saturation iD n Cox VGS VT (1 VDS )
2L
VDSSAT = VGS-VT if not otherwise stated in the parameter table
VT VT 0
Prof. Dr. Hoppe
2F VSB 2F
CMOS Analog Design
93
Passive components
Prof. Dr. Hoppe
CMOS Analog Design
94
Passive components for building analog circuits
in CMOS technology:
•
•
•
MOS technology – planar technology
Capacitors and resistors are compatible with MOS
technology fabrication steps
Inductors are not compatible
Prof. Dr. Hoppe
CMOS Analog Design
95
Capacitors:
•
•
Used more frequently in analog integrated circuits
than in discrete designs
Applications:
– compensation capacitors in amplifiers
– used in gain determining components in charge
amplifiers
– charge storage devices in switched capacitor
filters and digital to analog converters
Prof. Dr. Hoppe
CMOS Analog Design
96
Desired characteristics for capacitors:
•
•
•
•
•
Good matching accuracy
Low voltage coefficient
High ratio of desired capacitance to parasitic
capacitance
High capacitance per unit area
Low temperature dependence
Note: Analog CMOS processes meet these criteria, pure
digital processes do not!
Prof. Dr. Hoppe
CMOS Analog Design
97
Types of capacitances in analog CMOS processes:
(1) Poly Si / oxide / channel capacitor (MOS cap)
- like a gate capacitance of MOS transistor, but n+
implant introduced to form a well between „electrodes“
for this plate capacitor
Prof. Dr. Hoppe
CMOS Analog Design
98
Types of capacitances in analog CMOS processes:
(2) Poly / oxide / poly capacitor
- top and bottom plates are made up of poly silicon
Prof. Dr. Hoppe
CMOS Analog Design
99
Types of capacitances in analog CMOS processes:
(3) Metal 3 / oxide / metal 2 capacitor
- structure similar to the poly 2 / poly 1 capacitor
Prof. Dr. Hoppe
CMOS Analog Design
100
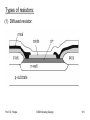
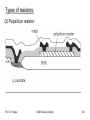
Types of resistors:
(1) Diffused resistor:
Prof. Dr. Hoppe
CMOS Analog Design
101
Types of resistors:
(1) Diffused resistor:
- Standard process: sheet resistance is in the range
50 Ω/sq to 150 Ω/sq
- Salicided process: surface layer on silicon containing
TaSi or TiSi compounds. Sheet resistance is in the
range 5 Ω/sq to 15 Ω/sq
- Problems:
(a) capacitance to n-well
(b) voltage coefficient 100....250 ppm/V
Prof. Dr. Hoppe
CMOS Analog Design
102
Types of resistors:
(2) Polysilicon resistor:
Prof. Dr. Hoppe
CMOS Analog Design
103
Types of resistors:
(2) Polysilicon resistor:
- surrounded by a thick oxide layer
- sheet resistance is in the range 30 Ω/sq to 200 Ω/sq,
depending on doping levels
- Polysilicide process: sheet resistance is around
10 Ω/sq
Prof. Dr. Hoppe
CMOS Analog Design
104
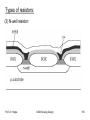
Types of resistors:
(3) N-well resistor:
Prof. Dr. Hoppe
CMOS Analog Design
105
Types of resistors:
(3) N-well resistor:
- n-well is not heavily doped, hence the sheet
resistance is high in the range 1 kΩ/sq to 10 kΩ/sq
- Voltage coefficient is very high, so it acts as a good
pull up resistor...but not suitable for generating a
precise voltage drop
Prof. Dr. Hoppe
CMOS Analog Design
106
Performance summary of passive components in
a 0.8 µm CMOS technology:
Component type
Range of
process
values
MOS cap
2.2 to 2.7
fF/µm2
0.05 %
50 ppm/K
50 ppm/V
Poly-poly cap
0.8 to 1.0
fF/µm2
0.05 %
50 ppm/K
50 ppm/V
M1-M2 cap
0.021 to
0.025 fF/µm2
1.5 %
-
-
P+ diffusion
resistor
80 to 150
Ω/sq
0.4 %
1500 ppm/K
200 ppm/V
Prof. Dr. Hoppe
Matching Temperature
accuracy coefficient
CMOS Analog Design
Voltage
coefficient
107
Performance summary of passive components in
a 0.8 µm CMOS technology:
Component type
Range of
process
values
n+ diffusion
resistor
50 to 80 Ω/sq
0.4 %
1500 ppm/K
200 ppm/V
Polysilicon
resistor
20 to 40 Ω/sq
0.4 %
1500 ppm/K
200 ppm/V
N-well resistor
1 to 2 kΩ/sq
?
8000 ppm/K
10,000
ppm/V
Prof. Dr. Hoppe
Matching Temperature
accuracy coefficient
CMOS Analog Design
Voltage
coefficient
108
Temperature dependence of
MOS devices
Prof. Dr. Hoppe
CMOS Analog Design
109
Temperature dependence of MOS components:
•
•
Temperature dependence of MOS components –
important performance characteristic in analog circuit
design
The temperature behavior of passive components is
usually expressed in terms of a fractional temperature
coefficient TCF defined as:
TCF = 1.dX
X dT
•
X can be resistance or capacitance of the passive
component. Usually TCF is multiplied by 106 and
expressed in units of part per million per oC
Prof. Dr. Hoppe
CMOS Analog Design
110
Temperature dependence of drain current iD of a
MOS transistor:
•
•
•
•
Most sensitive parameters in the drain current
equation are µ (mobility) and VT (threshold voltage)
Due to scattering at thermally induced lattice
vibrations, temperature dependence of µ is given as
µ = KµT -1.5
Temperature dependence of VT is approximated as
VT(T) = VT(T0) – α (T - T0)
α = 2.3 mV/oC and the expression is valid over the
range 200 - 400 K
In total iD decreases with increasing temperature
iD | 125 oC = 0.7 iD | 25 oC
Prof. Dr. Hoppe
CMOS Analog Design
111
Temperature dependence of reverse biased diode
current:
•
When VD < 0, the diode current is given as
-iD = Is = qA
(
)
Dppn0
Dnnp0
qAD .(ni)2
+
=
Lp
Ln
L
N
= KT3exp(- VG0 / Vt)
where D, L, N are diffusion constant, diffusion length and
impurity concentration of the dominant term (either n or p)
VG0 = band gap voltage of Si at 300 K (1.205V)
Vt = thermal voltage kT/q
Prof. Dr. Hoppe
CMOS Analog Design
112
Temperature dependence of reverse biased diode
current:
•
Differentiating with respect to T results in
dIs/dT = (3KT3/T)exp(-VG0 / Vt)
+ (qKT3VG0/KT2)exp(-VG0 / Vt)
3IS ISVG0
=
+
T
TVt
•
The TCF for the reverse diode current is
1 dIS 3 VG0
= +
IS dT T TVt
•
Reverse diode current doubles for every 5 oC increase
Prof. Dr. Hoppe
CMOS Analog Design
113
Example:
Calculate the TCF for the reverse diode current for 300 K
and Vt = 0.025 V
Prof. Dr. Hoppe
CMOS Analog Design
114
Analog CMOS subcircuits
Prof. Dr. Hoppe
CMOS Analog Design
115
MOS switch:
•
•
•
•
MOS switch – a very useful device
Analog circuits: the MOS switch is used in
multiplexers, modulation and switched capacitor
filters
Digital circuits: used in transmission gate logic,
dynamic latches, etc.
MOS transistor as a switch:
Prof. Dr. Hoppe
CMOS Analog Design
116
Model for a switch:
•
•
An ideal switch is a short circuit when ON and an
open circuit when OFF
Equivalent circuit for a voltage controlled non ideal
switch:
Prof. Dr. Hoppe
CMOS Analog Design
117
Model for a switch:
VC
= control voltage
A, B, C = terminals; C being the control terminal
rON
= ON resistance
rOFF
= OFF resistance (very high)
VOS
= offset voltage between A and B when the
switch is ON
IA, IB = leakage currents
IOFF
= offset current when the switch is OFF
CA, CB = parasitic capacitances at the terminals to GND
CAC, CBC = capacitive coupling between A and B,
contribute to the effect called charge
feedthrough – big problem in MOS switches!
Prof. Dr. Hoppe
CMOS Analog Design
118
ON resistance of a MOS switch:
•
•
•
•
rON consists of the series combination of rD, rS and
the channel resistance
rD, rS – parasitic drain and source resistances (~ 1Ω)
rchannel – channel resistance (~ 50Ω)....dominant!
Expression for small-signal channel resistance:
1
rON =
diD/dVDS
Q
L
=
K‘W(VGS - VT - VDS)
where Q designates the quiesent point of the
transistor
Prof. Dr. Hoppe
CMOS Analog Design
119
Range of voltages at the terminals of a MOS
switch compared to the gate (control) voltage:
•
•
•
•
•
nMOS: VG larger than the source to drain voltage to
switch the transistor ON (at least higher by VT)
pMOS: VG has to be less than the source to drain
voltage to switch the transistor ON
nMOS: Bulk has to be connected to the most
negative voltage
pMOS: Bulk has to be connected to the most
positive voltage
Consider nMOS switch:
VG = VDD , VBulk = VSS , then the transistor is ON until
VDD – VT >= VBA = VSD
Prof. Dr. Hoppe
CMOS Analog Design
120
Small signal on-resistance of a MOS switch as
a function of the Control Voltage:
Prof. Dr. Hoppe
CMOS Analog Design
121
Large signal behavior of the MOS-switch
For the NMOS-switch VDS must never exceed VGS-VT
Otherwise the device switches off and ron is in the
100kOhm range!
Hence the maximum voltage VDD or (any voltage
above VGS – VT) can never be transferred from drain
to source of a switch. Instead VDD –VT (a degraded
voltage) is observed at the output of the switch!
The corresponding abservations will be made for a
PMOS-switch!
Prof. Dr. Hoppe
CMOS Analog Design
122
Single stage amplifiers
Prof. Dr. Hoppe
CMOS Analog Design
123
Applications of CMOS amplifiers:
•
•
Analog applications:
- to overcome noise
- to drive a next stage
- used in feedback systems
- to provide logic levels for interfacing to digital
circuits
Digital applications:
- to drive a load
Prof. Dr. Hoppe
CMOS Analog Design
124
Basic notions:
•
Generalised system
transfer curve:
x may be current or
voltage
•
y(t) = α0 + α1x(t) + α2x2(t) + ...... + αnxn(t)
for x1 <= x <= x2
In a narrow range of x, y can be approximated with
a linear relationship:
y(t) ~ α0 + α1x(t)
where α0 = operating point
α1 = linear (small signal) gain
•
Prof. Dr. Hoppe
CMOS Analog Design
125
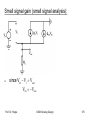
Basic notions:
•
•
•
•
If α1x(t) << α0, then the operating point OP is very
slightly disturbed and linearization around OP is
possible – small signal analysis
Δy = α1Δx : linear relationship between increments
of input and output
If x(t) varies over a large range, then the higher
order terms become important – large signal
analysis
If the slope of the characteristics varies with the
signal - Nonlinearity
Prof. Dr. Hoppe
CMOS Analog Design
126
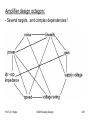
Competing design targets for amplifiers:
1.
2.
3.
4.
5.
6.
7.
8.
Gain
Speed
Power consumption
Supply voltage
Linearity
Noise
Maximum voltage swing at the output
Input and output impedance
Prof. Dr. Hoppe
CMOS Analog Design
127
Amplifier design octagon:
- Several targets...and complex dependencies !
Prof. Dr. Hoppe
CMOS Analog Design
128
Digital circuit design targets:
•
Three targets:
- die size
- speed
- power consumption
Prof. Dr. Hoppe
CMOS Analog Design
129
CMOS amplifiers
Prof. Dr. Hoppe
CMOS Analog Design
130
Basic principles:
•
•
MOSFET translates variations in its gate-source
voltage to a small signal drain current
If a resistive load is used, these current variations in
turn produce variations in the output voltage
Prof. Dr. Hoppe
CMOS Analog Design
131
Amplifier configurations:
1.
2.
3.
4.
5.
Common source stage (CS)
Source follower or common drain stage (SF)
Common gate stage (CG)
Cascode stage: cascade of CS and CG stage
Differential amplifiers
Prof. Dr. Hoppe
CMOS Analog Design
132
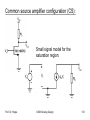
Common source amplifier configuration (CS):
Small signal model for the
saturation region:
Prof. Dr. Hoppe
CMOS Analog Design
133
Input – output characteristics:
1. Vin < VTH:
Vout = VDD
2. Vin >= VTH:
M1 is ON
saturation region
3. Vin >= Vout + VTH:
M1 in linear
region
Prof. Dr. Hoppe
CMOS Analog Design
134
Input – output characteristics:
1. Vin < VTH:
Vout VDD
2. Vin >= VTH:
1
W
2
Vout V DD R D n Cox
Vin VTH
2
L
3. Vin >= Vout + VTH:
Vout
1
W
2
2Vin VTH Vout Vout
VDD R D n Cox
2
L
Prof. Dr. Hoppe
CMOS Analog Design
135
Supressing short channel effects:
•
•
•
Analog circuits: Lmin of technology is not utilized.
Instead analog circuits use 4...5 times Lmin
For C35 process analog Lmin ~ 1.5 µm
Longer transistor length results in
(1) negligible subthreshold current
(2) small channel length modulation effect
(3) small velocity saturation effect
Prof. Dr. Hoppe
CMOS Analog Design
136
Deep triode region:
If Vin is high enough to drive M1 into deep triode region,
Vout << 2(Vin - VTH) and from the equivalent circuit
V out V DD
R
R
on
RD
Ron
on
R
D
VDD
1 RD / Ron
RD
1
W
nCox
V in V T VDS
L
Vout
Prof. Dr. Hoppe
V DD
W
1 n Cox R D V in V TH
L
CMOS Analog Design
137
Small signal gain:
•
In deep triode region, we have a voltage divider while in
the saturation region we have the proper amplifier
operation due to the quadratic dependence of the
current:
1
W
2
Vout V DD R D
Vin VTH
n Cox
2
L
•
The small signal gain is given as:
Vout
A
Vin
W
Vin VTH
R D n Cox
L
gmR D
Prof. Dr. Hoppe
CMOS Analog Design
138
Transconductance gm:
•
•
Small signal parameter
In saturation,
ID
VDS fixed
gm
Vin
W
VGS VTH
n Cox
L
2 ID
W
2 n Cox I D
L
VGS VTH
g m f VGS VTH
Prof. Dr. Hoppe
CMOS Analog Design
139
Transconductance gm:
•
•
Thus transconductance gm is dependent on input
voltage!
Gain A varies with Vin...Nonlinearity problem for
large signals!
Prof. Dr. Hoppe
CMOS Analog Design
140
How to maximize the voltage gain?
W
VRD
2
C
A
ID
n ox
L
ID
Where VRD is voltage drop across load resistance
W VRD
A 2 n Cox
L
ID
•
To increase the gain:
- make W/L larger
- make VRD large.... make RD large
- make ID smaller (make transistor weaker)
Prof. Dr. Hoppe
CMOS Analog Design
141
Trade-offs in maximizing the voltage gain:
•
•
•
Larger W/L larger input capacitance
Larger VRD smaller output swing
If VRD is kept constant ID has to be made smaller
RD must be increased
higher time constants at the output !
•
Trade-off: gain, BW, voltage swing !
Prof. Dr. Hoppe
CMOS Analog Design
142
Trade-offs in maximizing the voltage gain:
•
For large values of RD, the effect of channel length
modulation in M1 becomes significant
•
1
W
2
C
Vout VDD R D
Vin VTH 1 Vout
n ox
2
L
Vout
W
Vin VTH 1 Vout
R D n Cox
Vin
L
Vout
1
W
2
Vin VTH
R D n C ox
2
L
Vin
•
Using the approximation
I D 1 2 n Cox W LVin VTH
2
Prof. Dr. Hoppe
CMOS Analog Design
143
Trade-offs in maximizing the voltage gain:
We obtain:
A R Dg m R D I DA
•
Hence
gmR D
A
1 R D I D
•
Thus
Prof. Dr. Hoppe
decreases the amplification factor !
CMOS Analog Design
144
Small signal model for channel length modulation:
•
•
gmR D
A
1 R D I D
I D 1 rO ,
rO R D
A g m
rO R D
Since
Prof. Dr. Hoppe
CMOS Analog Design
145
Intrinsic gain:
•
•
Intrinsic gain = upperbound of the overall gain
Ideal current source infinite impedance
• lim R D , A g m
rO
rO
1
RD
results in
A g m rO
•
Todays technology:
gmrO is between 10 to 30
Prof. Dr. Hoppe
CMOS Analog Design
146
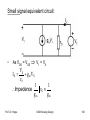
CS stage with diode connected load:
•
•
•
•
In MOS technology, resistors are complicated to
implement
Hence „active loads“ or so called „diode connected
transistors“ are used
MOSFET acts as small signal resistor when gate and
drain is shorted
Diode connected transistors are always in saturation
because VDS = VGS
Prof. Dr. Hoppe
CMOS Analog Design
147
Small signal equivalent circuit:
•
As VDS = VGS
V1 = VX
VX
IX
g m VX
rO
1
1
Impedence
rO
gm
gm
Prof. Dr. Hoppe
CMOS Analog Design
148
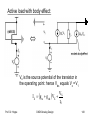
Active load with body effect:
Vx is the source potential of the transistor in
the operating point: hence Vbs equals Vx = V1
VX
I X g m g mb VX
rO
Prof. Dr. Hoppe
CMOS Analog Design
149
Active load with body effect:
•
VX
1
Impedance
IX g g 1
m
mb
rO
1
1
rO
g m g mb
g m g mb
•
Thus the body effect reduces the impedance !
Prof. Dr. Hoppe
CMOS Analog Design
150
Voltage gain of CS stage with diode connected
load:
•
For negligible λ,
1
A g m1
g m 2 g mb 2
g mb 2
g m1 1
where
gm2 1
gm2
•
Considering device dimensions,
A
Prof. Dr. Hoppe
2 n C ox W L 1 I D1
2 n C ox W L 2 I D 2
1
1
CMOS Analog Design
151
Voltage gain of CS stage with diode connected
load:
•
Since ID1 ID2 ,
A
Prof. Dr. Hoppe
W L 1 1
W L 2 1
CMOS Analog Design
152
CS stage with diode connected load – Large
signal analysis:
•
ID1 ID2
1
1
W
W
2
2
n Cox Vin VTH1 n Cox VDD Vout VTH 2
2
2
L 1
L 2
W
W
Vin VTH 1 VDD Vout VTH 2
L 1
L 2
Note: If VTH2 depends only slightly on Vout (weak body
effect), then we have a linear behavior and Vout is
proportional to Vin
Prof. Dr. Hoppe
CMOS Analog Design
153
CS stage with diode connected load – Large
signal analysis:
•
Differentiating both sides w.r.t Vin
W
W Vout VTH 2
Vin
L 1
L 2 Vin
•
With application of the chain rule
Vout
VTH 2 VTH 2 Vout
Vin Vout Vin
Vin
we get
Vout
A
Vin
Prof. Dr. Hoppe
W L 1 1
W L 2 1
CMOS Analog Design
The result matches
with the small
signal analysis !
154
Input / output characteristics of active load CS
stage:
•
•
At point A, M1 enters the triode region (strong
nonlinearity !)
Above VTH1 and below VA,
Vout Vin (linear behavior)
Prof. Dr. Hoppe
CMOS Analog Design
155
CS stage with pMOS active load:
•
•
•
•
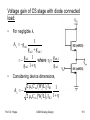
To improve amplification we use CS
stage with pMOS active load
pMOS output node can charge upto
full VDD .....more voltage swing !
No body effect 0
A
•
n W L 1
p W L 2
Gain depends very weakly on device dimensions
Prof. Dr. Hoppe
CMOS Analog Design
156
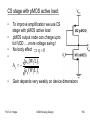
CS-Stufe mit pMOS-Last
Ausgangsspannungsbereich
•
Vout(max) = VDD – Vtp
•
Vout(min): komplizierter:
Vout(min)
VDD
vds1 vgs1 Vtn vout vin Vtn
M1 ungesättigter Bereich:
v ²
v ²
W
W
id 1 µnCox ((vgs1 Vtn )vds1 ds1 ) µnCox ((vDD Vtn )vout out )
L
2
L
2
id 2
Prof. Dr. Hoppe
µ p Cox W
µ p Cox W
(vsg 2 Vtp )²
(vDD vout Vtp )²
2 L
2 L
CMOS Analog Design
157
CS-Stufe mit pMOS-Last
Ausgangsspannungsbereich: Gleichsetzen
•
id1 = id2 und auflösen nach Vout
ergibt
VDD VT
vout (min) VDD VT
µ pW p
1
µnWn
Annahme: Einsatzspannung von pMOS (Betrag) und
nMOS gleich VT
Prof. Dr. Hoppe
CMOS Analog Design
158
CS-Stufe mit pMOS-Last
Verstärkung A = Vout/Vin und
Ausgangswiderstand Rout:
Aufsummieren aller Ströme, die in den
Ausgangsknoten fließen:
0 gm1vin gds1vout gm 2vout gds 2vout
Vout
g m1
µn COX W1 L2
Vin g ds1 g m 2 g ds 2
µ p COX W2 L1
1
1
Rout
gds1 gm 2 gds 2 gm 2
Prof. Dr. Hoppe
CMOS Analog Design
159
CS-Stufe mit pMOS-Last
3dB Frequenz: Verstärkung sinkt hier auf 70%:
-3dB = 1/[Rout(Cout)]
•
Cout ist die gesamte kapazitive Last am Ausgang:
– Externe Eingangskapazität
– Leitungskapazität
– Parasitäre Transistorkapazitäten
Beispiel: Rout = ro für einen pMOS-Transistor W/L = 3/1, in
dem der Drainstrom 60µA fließt ist bei Cout = 5 pF:
1/ ro gm 2µ p Cox (W / L) I D 2 60 3 50µA / V 134µA / V
roC 5 pF /134µA / V 0,037 106 s
3dB 27 Mrad / s f 3dB 4,3MHz
Prof. Dr. Hoppe
CMOS Analog Design
160
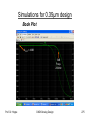
AMS 0,35µm CMOS Technology
AMS CSD 0,35µm CMOS 3,3V Prozess
Parameter
Beschreibung
Parameterwerte
NMOS
PMOS
Einheit
Vth0
Einsatzspannung VBS = 0
0,5 0,05 -0,65 0,5
V
K’
Transistorleitwert
175 10% 60 10%
µA/V2
Substratsteuerfaktor
0,58
V1/2
Kanallängenmodulationsfaktor
0,06L=1µm 0,06 L=1µm
0,04L=2µm 0,04 L=2µm
V-1
2F
Oberflächenpotential
starker Inversion
0,8
V
bei
0,42
0,8
*Level 1 SPICE Modell CSD 0,35
.MODEL MOSN NMOS VTO=0.5 KP=175U GAMMA=0.58 LAMBDA=0.06 PHI= 0.8
.MODEL MOSP PMOS VTO=-0.65 KP=60U GAMMA=0.42 LAMBDA=0.06 PHI=0.8
Prof. Dr. Hoppe
CMOS Analog Design
161
CS-Stage with pMOS-Load
NMOS: W/L =5.5 PMOS = 1.0 CSD technology
*Common Source Amplifier
VDD 1 0 DC 3.3
VIN 2 0 DC 0
MP out out 1 1 MODP W = 1U L = 1U
MN out 2 0 0 MODN W = 5.5U L = 1U
CL out 0 5P
.model MODN NMOS VTO=0.5 KP=175U GAMMA=0.58 LAMBDA=0.06 PHI= 0.8
.MODEL MODP PMOS VTO=-0.65 KP=60U GAMMA=0.42 LAMBDA=0.06
PHI=0.8
.DC VIN 0.0 3.3 5U
.PRINT DC V(out) V(in)
.END
Prof. Dr. Hoppe
CMOS Analog Design
162
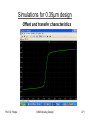
CS-Stage with pMOS-Load
NMOS: W/L =5.5 PMOS = 1.0 CSD technology
Prof. Dr. Hoppe
CMOS Analog Design
163
CS-Stage with pMOS-Load
NMOS: W/L =5.5 PMOS = 1.0 CSD technology
*Common Source Amplifier
VDD 1 0 DC 3.3
VIN 2 0 DC 0.9 AC 1.0
MP out out 1 1 MODP W = 1U L = 1U
MN out 2 0 0 MODN W = 5.5U L = 1U
CL out 0 5P
.model MODN NMOS VTO=0.5 KP=175U GAMMA=0.58 LAMBDA=0.06 PHI= 0.8
.MODEL MODP PMOS VTO=-0.65 KP=60U GAMMA=0.42 LAMBDA=0.06 PHI=0.8
*.DC VIN 0.0 3.3 5U
.AC DEC 20 100 10MEG
.PRINT AC VDB(out)
.END
Prof. Dr. Hoppe
CMOS Analog Design
164
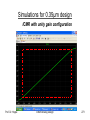
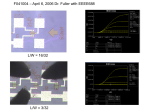
CS-Stage with pMOS-Load
NMOS: W/L =5.5 PMOS = 1.0 CSD technology
Prof. Dr. Hoppe
CMOS Analog Design
165
CS-Stufe mit pMOS-Last
Designrezeptur: W zu L bei geg. Verstärkung
Hängt von den Vorgaben ab. In der Regel wird eine
Verstärkung vorgegeben, aus der sich alles weitere
ableitet.
Im Labor werden wir einen Verstärker entwerfen, der eine
Verstärkung von A = - 4 haben soll. Daraus folgt:
Aus Gleichung auf Folie 155 folgt dann ein
Weitenverhältnis für pMOS- und nMOS-Transistor.
Nächster Schritt ist dann zu verifizieren, dass die
Verstärkung auch tatsächlich erreicht wird. Dazu ist die
Kennlinie also Vout = f(Vin) aufzunehmen.
Die Verstärkung folgt dann als Ableitung von Vout nach Vin
Prof. Dr. Hoppe
CMOS Analog Design
166
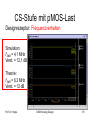
CS-Stufe mit pMOS-Last
Designrezeptur: Arbeitspunkt
Aus der simulierten Verstärkung folgt dann der
Arbeitspunkt, der implizit für die Kleinsignalanalyse
verwendet wurde, aus der die Formel für A stammt.
Aus der VerstärkungskennLinie kann nun der Arbeitspunkt abgelesen werden:
Kennlinie
Vin = 0,67V / Vout = 1,91V
Verstärkung
Prof. Dr. Hoppe
CMOS Analog Design
167
CS-Stufe mit pMOS-Last
Designrezeptur: Output Swing
Aus der Verstärkungskennlinie kann die minimale und
maximale Ausgangsspannung abgelesen werden:
Simulation:
Vout(max) = 2,98V
Vout(min) = 0,06V
Theorie:
Vout(max) = 2,8V
Vout(min) = 0,08V
Prof. Dr. Hoppe
CMOS Analog Design
168
CS-Stufe mit pMOS-Last
Designrezeptur: Frequenzverhalten
Am Arbeitspunkt können wir den Strom in M1 und damit in
M2 ausrechnen
damit folgt gm2 (Eingangsleitwert
pMOS)
Wp
2
1
iD1 iD 2 µ pCox
VgsPMOS ( Arbeitspunkt ) VTp
2
Lp
g m 2 2µ p Cox (W / L) p I D
roC C / g m 2
3dB
Prof. Dr. Hoppe
g m 2 rad
3dB
f 3dB
Hz
C s
2
CMOS Analog Design
169
CS-Stufe mit pMOS-Last
Designrezeptur: Frequenzverhalten
Simulation:
f-3dB = 4,1 MHz
Verst. = 12,1 dB
Theorie:
f-3dB = 6,2 MHz
Verst. = 12 dB
Prof. Dr. Hoppe
CMOS Analog Design
170
Source follower:
•
•
CS stage has a good voltage gain, but load impedance
has to be high
If the load impedance is low, a „buffer“ is needed for
impedance matching
Prof. Dr. Hoppe
CMOS Analog Design
171
Source follower:
•
Source follower (or „common drain stage“) may
operate as a voltage buffer
Prof. Dr. Hoppe
CMOS Analog Design
172
Source follower – input/output characteristics:
•
Vout follows Vin with a voltage difference (level shift)
equal to VGS
Vout
Prof. Dr. Hoppe
1
W
2
Vin VTH Vout R S
n Cox
2
L
CMOS Analog Design
173
Small signal gain (large signal analysis):
Vout
•
1
W
Vin VTH Vout 2 R S
n Cox
2
L
Differentiating both sides w.r.t. Vin
VTH Vout
Vout 1
W
R S
n Cox
2 Vin VTH Vout 1
Vin 2
L
Vin Vin
Vout
VTH
• since
Vin
Vin
W
n Cox
Vin VTH Vout R S
Vout
L
Vin 1 C W V V V R 1
n ox
in
TH
out
S
L
Prof. Dr. Hoppe
CMOS Analog Design
174
Small signal gain (large signal analysis):
•
W
With g m n Cox
Vin VTH Vout we get:
L
gmRS
A
1 g m g mb R S
Prof. Dr. Hoppe
CMOS Analog Design
175
Small signal gain (small signal analysis):
•
since Vin V1 Vout
Vbs Vout
Prof. Dr. Hoppe
CMOS Analog Design
176
Small signal gain (small signal analysis):
Vout
g m1V1 g mb 1Vout
•
RS
Vout
A
will result in
Vin
gmRS
A
1 g m g mb R S
•
Maximum possible gain = 1
Prof. Dr. Hoppe
CMOS Analog Design
177
Drawback of RS implemented as ohmic resistor:
•
•
•
•
ID1 depends strongly on input DC level
If Vin changes from 1.5 to 2.0 V (10 % increase)
then ID1 increases by a factor of „2“
Hence VGS – VTH increases by √2
highly non linear I/O characteristics !
Improvement: instead of RS we take
a constant current source M2 to get
a linear behavior
Prof. Dr. Hoppe
CMOS Analog Design
178
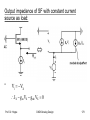
Output impedance of SF with constant current
source as load:
•
V1 VX
I X g m VX g mb VX 0
Prof. Dr. Hoppe
CMOS Analog Design
179
Output impedance of SF with constant current
source as load:
VX
1
R out
• Hence
IX
g m g mb
•
Note: Body effect decreases the output resistance of the
source follower !
Prof. Dr. Hoppe
CMOS Analog Design
180
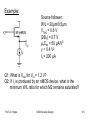
Example:
Source follower:
W/L = 20µm/0.5µm
VTH0 = 0.6 V
|2ΦF| = 0.7 V
µnCox = 50 µA/V2
γ = 0.4 V2
I1 = 200 µA
Q1: What is Vout for Vin = 1.2 V?
Q2: If I1 is produced by an nMOS device, what is the
minimum W/L ratio for which M2 remains saturated?
Prof. Dr. Hoppe
CMOS Analog Design
181
Solution A1:
•
VTH depends on Vout
Iterative solution:
(1) we calculate Vout for VTH0
(2) we calculate VTH for Vout obtained in (1)
1
W
2
I D n C ox Vin VTH Vout
2
L
2I D
2
Vin VTH Vout
W
n C ox
L
2*200 A 2
2
1.2 0.6 Vout
V
50 A *40
Prof. Dr. Hoppe
CMOS Analog Design
182
Solution A1:
Vout 0.153 V
•
Now,
VTH VTH 0 2F VSB 2F
VTH 0.6 0.4 0.7 0.153 0.7
0.635 V
•
•
Using the new VTH the improved value of Vout is 0.119 V,
which is approximately 35 mV less than the calculated
value.
The next iterations yield VTH = 0.635V 0.627V and
Vout = 0.117V 0.125V
Prof. Dr. Hoppe
CMOS Analog Design
183
Solution A2:
•
•
•
•
Consider transistor in place of current source:
Drain-source voltage of M2 is 0.119 V
Device is saturated only if VGS – VTH < 0.119 V
In the saturation region we have,
1
W
2
I D 200 A n Cox 0.119
2
L 2
283 m
W
L 2 min 0.5 m
Prof. Dr. Hoppe
CMOS Analog Design
184
Drawbacks of the SF configuration:
•
Source followers exhibit a high input impedance and a
moderate output impedance, but at the cost of two
drawbacks:
(1) nonlinearity
(2) voltage headroom limitation
Prof. Dr. Hoppe
CMOS Analog Design
185
Nonlinearity of the SF configuration:
•
•
•
•
Even with an ideal current source I1 the I/O
characteristics display a nonlinearity due to the
dependence of VTH on Vsource
Submicron technology: rO of the transistor also changes
with VDS additional nonlinear effects !
Nonlinearity due to body effect can be eliminated if the
bulk is tied to the source
Because all nMOS devices have a common bulk
potential, this is only possible for pMOS devices in a
n-well technology
Prof. Dr. Hoppe
CMOS Analog Design
186
Nonlinearity of the SF configuration:
•
pMOS source follower with no body effect:
•
Price paid: PFET have a lower carrier mobility leading to
higher output impedance than for a nMOS source
follower
Prof. Dr. Hoppe
CMOS Analog Design
187
Voltage headroom limitation of SF:
•
Source followers shift the level of the signal by VGS
consuming voltage headroom and hence limiting the
voltage swing
Prof. Dr. Hoppe
CMOS Analog Design
188
Voltage headroom limitation of SF:
•
•
•
Without source follower: Vmin at node X is VGS1 – VTH1 for
having M1 in saturation
With the source follower: Vmin at node X should be
greater than VGS2 + (VGS3 – VTH3) so that M3 is in
saturation
For same overdrive voltages in M1 and M3, voltage
swing allowable at X is reduced by VGS2
Prof. Dr. Hoppe
CMOS Analog Design
189
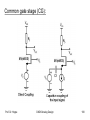
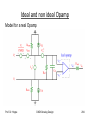
Common gate stage (CG):
Prof. Dr. Hoppe
CMOS Analog Design
190
Common gate stage (CG):
•
•
•
•
•
In the CS-Stage and for Source-Followers input signal is
applied to a gate of a MOSFET.
If the input is applied to the source terminal of a
MOSFET and output is taken at the drain terminal we
have a Comon Gate Stage
Gate is connected to a dc voltage to establish proper
operating conditions
Bias current flows directly through input signal source
– direct coupling
M1 can be biased by a constant current source, with the
signal capacitively coupled to the circuit
– capacitive coupling
Prof. Dr. Hoppe
CMOS Analog Design
191
Direct coupling – Large signal analysis:
•
•
•
Assume that Vin decreases from a large positive value
Vin >= Vb – VTH: M1 is off and Vout = VDD
For lower values of Vin: M1 goes into saturation
1
W
2
Vb Vin VTH
I D n Cox
2
L
•
As Vin decreases, so does Vout, eventually driving M1 into
the triode region if
1
W
Vb Vin VTH 2 R D Vb VTH
VDD n Cox
2
L
Prof. Dr. Hoppe
CMOS Analog Design
192
CG input – output characteristics:
•
If M1 is saturated, output voltage can be expressed as:
Vout
1
W
Vb Vin VTH 2 R D
VDD n Cox
2
L
Prof. Dr. Hoppe
CMOS Analog Design
193
CG stage small signal gain:
•
Small signal gain can be obtained by differentiating w.r.t.
Vin
Vout
W
VTH
n Cox Vb Vin VTH 1
Vin
L
Vin
•
R D
Since VTH Vin VTH VSB , we have
Vout
W
n Cox
R D Vb Vin VTH 1
Vin
L
A g m 1 R D
Prof. Dr. Hoppe
Gain is positive !
CMOS Analog Design
194
CG stage input impedance:
•
For λ = 0, the impedance seen at the source of M1 is the
same as the output impedance in the case of source
follower
1
1
g m g mb g m 1
•
•
Thus, the body effect decreases the input impedance!
Low input impedance is useful for certain applications
Prof. Dr. Hoppe
CMOS Analog Design
195
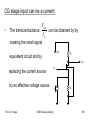
CG stage input can be a current:
•
Vout
The transconductance
can be obtained by by
I in
creating the small signal
VDD
equivalent circuit and by
RD
Vout
replacing the current source
by an effective voltage source.
Prof. Dr. Hoppe
CMOS Analog Design
Vb
Iin
Rp
196
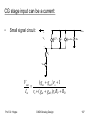
CG stage input can be a current:
•
Small signal circuit:
Vout
+
V1
gmV1
ro
gmbVbs
RD
_
Rp
Vin
Vout
( g m g mb )ro 1
I in ro ( g m g mb )ro RP RD
Prof. Dr. Hoppe
CMOS Analog Design
197
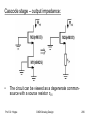
Cascode stage:
•
•
Input signal of a CG-stage may be a current
A common source stage converts a voltage signal
into a current signal
• Cascade of a common source and a common gate
stage is called a „cascode stage“
• A cascode (cascaded triode, vacuum tube days)
offers advantages over simple CS-stages:
1. High output impedance!
2. High voltage gain!
Prof. Dr. Hoppe
CMOS Analog Design
198
Cascode stage:
•
•
•
•
•
•
Prof. Dr. Hoppe
Cascade of a common
source and a common
gate stage is called a
„cascode stage“
M1 generates small signal
drain current proportional
to Vin
M2 routes this current to
RD
M1 is the input device
M2 is the cascode device
M1 and M2 carry the same
current
CMOS Analog Design
199
Cascode stage bias conditions:
•
•
•
M1 is saturated if VX >= Vin – VTH1
To keep M1 and M2 both in saturation,
VX = Vb – VGS2
Hence, Vb – VGS2 >= Vin – VTH1
Or Vb = Vin + VGS2 – VTH1
•
•
M2 in saturation Vout >= Vb – VTH2
Hence Vout >= Vin – VTH1 + VGS2 – VTH2
•
If Vb is chosen to keep M1 at the edge of saturation,
minimum output voltage for which both transistors
operate in saturation is equal to the overdrive voltage of
M1 plus that of M2
Prof. Dr. Hoppe
CMOS Analog Design
200
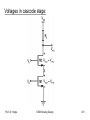
Voltages in cascode stage:
Prof. Dr. Hoppe
CMOS Analog Design
201
Cascode stage – large signal analysis:
•
•
Vin = 0 V
Vin < VTH1
•
Vin >= VTH1
•
Vin sufficiently
large
Prof. Dr. Hoppe
Vout = VDD
M1 and M2 are „off“
Vout = VDD
VX = Vb – VTH2
M1 is „on“
Vout drops as M1 draws current
VGS2 increases as ID2 increases
hence VX drops
VX drops below Vin by VTH1
- M1 enters triode region
Vout drops below Vb by VTH2
- M1 and M2 are in triode region
CMOS Analog Design
202
Cascode stage – large signal analysis:
•
Main advantages of cascode structure:
- high output impedance
2
- high voltage gain proportional to g m
Prof. Dr. Hoppe
CMOS Analog Design
203
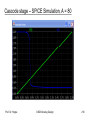
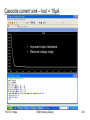
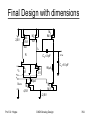
Cascode stage – SPICE-Simulation
•
•
AMS C35 with pull-up 3/1, NMOS Transistors 30/1
VBIAS = VDD/2
Prof. Dr. Hoppe
CMOS Analog Design
204
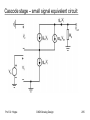
Cascode stage – small signal equivalent circuit:
Prof. Dr. Hoppe
CMOS Analog Design
205
Cascode stage – output impedance:
•
The circuit can be viewed as a degenerate commonsource with a source resistor rO1
Prof. Dr. Hoppe
CMOS Analog Design
206
Cascode stage – output impedance:
•
Using the equation of output resistance for common
source stage,
R out 1 g m 2 g mb 2 rO 2 rO1 rO 2
•
•
Assuming g m rO
1 , we have
R out g m 2 g mb 2 rO 2 rO1
M2 boosts the output impedance of M1 by a factor of
g m2 g mb 2 rO2 !!
Prof. Dr. Hoppe
CMOS Analog Design
207
Cascode stage – voltage gain:
•
Voltage gain of a cascode stage is given as:
A gm1 gm2 gmb2 rO 2 rO1
•
•
•
The maximum voltage gain is roughly equal to the
square of the intrinsic gain of the transistors
High output impedance of the cascode stage results in a
high voltage gain !
A simplified formula without body effect:
A
gm1
2 K N '(W1 / L1 )
gds 3
3P 2 I
Transistor „3“ is a PMOS-Fet connected to Vdd implementing
the pull-up-resistor
Prof. Dr. Hoppe
CMOS Analog Design
208
Cascode stage – Design Procedure:
•
The following relations determine the properties of the
amplifier:
Prof. Dr. Hoppe
CMOS Analog Design
209
Cascode stage – Design Procedure:
•
For cascode amplifiers we have the folllowing design
parameters:
1. The W/L-ratios for three transistors
2. The dc current I
3. The bias voltages
•
Typical specifications are: supply voltage VDD, small
signal gain A, the max. and min. output voltage swing
vout(max) and vout(min), and the power dissipation P
•
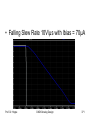
Example: VDD = 3,3V, A =-50 V/V, P = 1mW, Vout(max) =
2,8V and Vout(min) = 1,4V, Slew Rate 10V/µs @ 10pF
Prof. Dr. Hoppe
CMOS Analog Design
210
AMS 0,35µm CMOS Technology
AMS CSD 0,35µm CMOS 3,3V Prozess
Parameter
Beschreibung
Parameterwerte
NMOS
PMOS
Einheit
Vth0
Einsatzspannung VBS = 0
0,5 0,05 -0,65 0,5
V
K’
Transistorleitwert
175 10% 60 10%
µA/V2
Substratsteuerfaktor
0,58
V1/2
Kanallängenmodulationsfaktor
0,06L=1µm 0,06 L=1µm
0,04L=2µm 0,04 L=2µm
V-1
2F
Oberflächenpotential
starker Inversion
0,8
V
bei
0,42
0,8
*Level 1 SPICE Modell CSD 0,35
.MODEL MOSN NMOS VTO=0.5 KP=175U GAMMA=0.58 LAMBDA=0.06 PHI= 0.8
.MODEL MOSP PMOS VTO=-0.65 KP=60U GAMMA=0.42 LAMBDA=0.06 PHI=0.8
Prof. Dr. Hoppe
CMOS Analog Design
211
Cascode stage – Design Procedure:
1. P sets an upper bound 1mW/3,3V = 330µA, Slew Rate
sets a lower bound 100µA: We take I = 200µA
2. We calculate (W/L)3 since all other numbers are known in
the relation for M3 in the figure
W3
2I
400µA
26,7
L3 K P '(VDD vout (max))2 60µA / V 2 (3.3 2.8)2V 2
•
The current source on the upper left-hand side has the
same dimensions if IBIAS = I
3. Next we obtain (W/L)1 from the relation on the lower right
of the figure
2
2
W1 A I 50 0.06 200µA
L1
Prof. Dr. Hoppe
2KN '
2 175µA / V
CMOS Analog Design
2
51,5
212
Cascode stage – Design Procedure:
4. Next we calculate (W/L)2
•
First we need VDS1(sat) and use the vout(min)-spec to
obtain VDS2(sat)
vDS 1 ( sat )
2I
400µA
0,67V
2
K N '(W1 / L1 )
175µA / V 51,5
•
Subtracting this figure from 1.4V yields VDS2(sat)=0.73V
•
Therefore
W2
2I
400µA
4,3
2
2
2
L2 K N 'VDS 2 ( sat ) (0,73) 175µA / V
Prof. Dr. Hoppe
CMOS Analog Design
213
Cascode stage – Design Procedure:
5. At last we need the bias voltage VGG2
•
First we need VDS1(sat) and use the vout(min)-spec to
obtain VDS2(sat)
VGG 2
2I
400µA
VDS 1 ( sat )
VTN 0.67V
K N '(W2 / L2 )
175µA / V 2 (4.3)
0.67V 0.73V 0.50V 1.90V
Prof. Dr. Hoppe
CMOS Analog Design
214
Cascode stage – SPICE Netlist:
*CS-Stage transfer characteristic
Vdd 3 0 DC 3.3V
Vin 1 0 DC 0V
VGG2 4 0 DC 1.9V
IBIAS 10 0 DC 200U
Cl 2 0 10P
M3 2 10 3 3 MOSP W = 26.7U L = 1U
M3B 10 10 3 3 MOSP W = 26.7U L = 1U
M2 2 4 41 0 MOSN W = 4.3U L = 1U
M1 41 1 0 0 MOSN W = 51.5U L = 1U
*Level 1 SPICE Modell CSD 0,35
.MODEL MOSN NMOS VTO=0.5 KP=175U GAMMA=0.58 LAMBDA=0.06 PHI= 0.8
.MODEL MOSP PMOS VTO=-0.65 KP=60U GAMMA=0.42 LAMBDA=0.06 PHI=0.8
.dc lin Vin 0V 3.3V 0.01V
.Plot(V2)
.end
Prof. Dr. Hoppe
CMOS Analog Design
215
Cascode stage – SPICE Simulation, A = 80
Prof. Dr. Hoppe
CMOS Analog Design
216
Current sources
Prof. Dr. Hoppe
CMOS Analog Design
217
Practical current source:
•
•
For an ideal current source rO and Iout is constant for
all output voltages
Normally rO is finite and Iout = f(Vout)
Prof. Dr. Hoppe
CMOS Analog Design
218
Requirements of a good performance current mirror:
•
•
•
•
The current-ratio is precisely set by the aspect-ratio
(W/L) and is independent of temperature
Output impedance is very high, i.e., very high Rout and
very low Cout. As a result, the output current is
independent of output voltage (DC and AC)
Input resistance Rin is very low
The voltage compliance is low, i.e., the minimum output
voltage Vout, for which the output acts as a current
source, is low
Prof. Dr. Hoppe
CMOS Analog Design
219
Basic current mirror:
•
•
M1 is diode connected transistor which is always in
saturation
ID1 is mirrored into transistor M2
Prof. Dr. Hoppe
CMOS Analog Design
220
Basic current mirror:
•
W1 W2
Since VGS1 = VGS2 and if
I D1 I D 2
L1 L 2
provided the channel length modulation effects are very
small
•
•
1
W1
2
VGS1 VTH
I D1 n Cox
2
L1
1
W2
2
VGS2 VTH
I D 2 n Cox
2
L2
Since VGS1 = VGS2 , I D 2
I D1
Prof. Dr. Hoppe
W2 L1 W/L ratios determine
W1L 2 ID2 !
CMOS Analog Design
221
Basic current mirror:
•
W L2
Iout
I REF
W L1
OR
where I REF
•
What is the minimum voltage across M2 such that M2
remains in saturation?
- V V V V V
out
•
VDD VGS VSS
I D1
RD
min
GS2
TH
DS2
What is the output resistance?
-
rO 2
Prof. Dr. Hoppe
1
1
1
g m 2 I out I D 2
where λ is channel
length modulation factor
CMOS Analog Design
222
Basic current mirror – design example:
•
5 design variables: L1, W1, L2, W2, and R = f(VGS)
•
If we test 10 values per design parameter per simulation,
then we need 105 simulations !
Strategy:
step (1): Select a common channel length such that λ is
very small
•
I D1 W1
L1 = L2 = L
I D 2 W2
λ = f(L) should be as small as possible
therefore L >> Lmin
Note: For AMS CSD Lanalog = 1 µm
Prof. Dr. Hoppe
CMOS Analog Design
223
Basic current mirror – design example:
•
step (2): Select VGS
VGS is chosen close to VTH in order to have reasonable
currents in large devices
VGS – VTH = ΔV is „overdrive“ or excess voltage
n-channel device p-channel device
Parameter
0.5
-0.65
VTH (V)
0.58
0.42
175
60
0.06
0.06
Prof. Dr. Hoppe
CMOS Analog Design
V
Cox A V 2
λ (1/V) for L = 1µm
224
Basic current mirror – design example:
•
For a reasonable overdrive voltage say, ΔV = 0.2V, we
get VGS = VTH + ΔV = 0.7 V
•
step (3): Calculate R
VDD VGS VSS
R
I D1
For example: to design a current mirror ID1 = ID2 = 10 µA
the required R can be calculated as
3.3 0.7 0
2.6
R
260 k
10 A
10 A
Prof. Dr. Hoppe
CMOS Analog Design
225
Basic current mirror – design example:
•
How to implement R = 260 kΩ ?
sheet resistance: N-well: 1 kΩ per square
NDIFF: 180 Ω per square
PDIFF: 160 Ω per square
Note: On-chip resistance of such a high value is not
possible to implement. To overcome this we usually use
externally connected resistances to the IC pins
•
step (4): Calculate W1 and W2
1 W1
A
2
I D1
n Cox 2 * 0.7 0.5 10 A
2 L1
V
175 A
W1
2
10 A
2 * 0.04 V *
2 V
1 m
Prof. Dr. Hoppe
CMOS Analog Design
226
Basic current mirror – design example:
W1 W2 2.85 m 3 m
•
step (5): Calculate Vmin
VDS2 VGS VTH
Vmin Vout V 0.2 V
Note: Thus, the minimum output voltage = overdrive
voltage selected by the designer
•
step (6): Calculate rout
rout
1
1
1.67 M
I D 2 0.06 (1 V) *10 A
Prof. Dr. Hoppe
CMOS Analog Design
227
Basic current mirror – design example:
Design Example: 5/1 Current Mirror using Iref = 10µA
Prof. Dr. Hoppe
CMOS Analog Design
228
Basic current sink
Overdrive = 0.2V
50µA current
Output resistance
350kOhm
Prof. Dr. Hoppe
CMOS Analog Design
229
Cascode current mirrors:
•
•
•
In practice, channel length modulation effect results in
significant error in copying currents
While VDS1 = VGS1 = VGS2, VDS2 may not equal VGS2
because of the circuitry fed by M2
In order to suppress the effect of channel length
modulation, a cascode current source can be used
Prof. Dr. Hoppe
CMOS Analog Design
230
Cascode curent mirrors:
•
•
•
Prof. Dr. Hoppe
If Vb is chosen such that
VY = VX, then Iout closely
tracks IREF
This is because the
cascode device „shields“
the bottom transistor from
variations in Vp
Thus, we say that VY
remains close to VX and
hence ID2 = ID1 with high
accuracy
CMOS Analog Design
231
Cascode curent mirrors:
•
•
How do we generate Vb?
Since the objective is to ensure VY = VX, we must
guarantee Vb – VGS3 = VX or Vb = VGS3 + VX
•
•
Prof. Dr. Hoppe
This result suggests that if
a gate source voltage is
added to VX, the required
value of Vb can be
obtained
The idea is to place
another diode connected
device M0 in series with
M1, thereby generating a
voltage VN = VGS0 + VX
CMOS Analog Design
232
Cascode curent mirrors:
•
Proper choice of the dimensions of M0 w.r.t. M3 yields
VGS0 = VGS3
• Connecting node N to the
gate of M3 we have
VGS0 + VX = VGS3 + VY
•
If the transistor dimensions
are properly matched, then
we get VX = VY
•
This result holds even if
M0 and M3 suffer from
body effect
Voltage range: Vmin is 2*V
Output resistance: gm2rds3
•
•
Prof. Dr. Hoppe
CMOS Analog Design
233
Cascode current sink – Iout = 10µA
vdd5500DC
DC3.3
3.3
vdd
• Improved
output resistance
RL5522260000
190000
RL
• Reduced
voltage
Vout4400DC
DC10.0
3.3 range
Vout
m12222010
0 MODN
= 16U
L 1U
= 1U
m1
0 MODN
WW
= 16U
L=
m24422012
0 MODN
= 16U L
L=
= 1U
1U
m2
0 MODN
WW
= 36.3U
m3 10 10 0 0 MODN W = 16U L = 1U
m4 12 10 0 0 MODN W = 16U L = 1U
Prof. Dr. Hoppe
CMOS Analog Design
234
Differential Amplifiers
Prof. Dr. Hoppe
CMOS Analog Design
235
Why Differential Amplifiers?
• Differential amplifiers are versatile building
blocks in analog circuits:
– Input stages of Operational amplifiers
– Read amplifier in SRAMs
– Noise and crosstalk immune signal
processing
– Low voltage data transfer
Prof. Dr. Hoppe
CMOS Analog Design
236
Why Differential Signals?
Clock
Coupling
Prof. Dr. Hoppe
Signal
• Differential signals
are immune with
respect to crosstalk
effects as „+“ and „-“
signals are affected
in an identical
fashion!
CMOS Analog Design
237
Principles of Differential Amplifiers
•
Differential amplifier may be
formed by two CS-stages.
•
Problem im input voltage is
too low on one side, then
the corresponding CS-stage
is switched off!
output voltage is clipped
nonlinear behaviour
Prof. Dr. Hoppe
CMOS Analog Design
238
Principles of Differential Amplifiers
• Solution the two CSstages are sourcecoupled by a current
source
• No clipping of output
voltage but slight
nonlinearities for low
input common mode
voltages!
Obviously the gain
vanishes for lager
input voltage
differences!
Prof. Dr. Hoppe
CMOS Analog Design
239
Key parameters of Differential Amplifiers
Gain (of course)
Input Common Mode Range: linear operation until one of the
transistors leaves saturation!
ICMR: Input Common Mode Range (ca. 50% VDD-VSS)
Offset:
Transistors M1 and M2 are not completely identical due to
process variations
Vin1 = Vin2 not necessarily Vout1 = Vout2
but Vout1 = Vout2 if and only if Vin1 = Vin2 + Vos
Vos = Input-Offset-Voltage (typ. 5 - 20 mV)
Prof. Dr. Hoppe
CMOS Analog Design
240
Common Mode Amplification
Common Mode Voltages should not be
amplified!
Only Differential Voltages are of interest!
Common mode gain AvC = 0!
Vout1 Vout 2 A D (Vin1 Vin 2 ) A C
Differential
Gain
Prof. Dr. Hoppe
Vin1 Vin 2
2
Common
Mode Gain
CMOS Analog Design
241
Common Mode Amplifification
Common Mode Voltage VinCM
applied to the amplifier inputs
reduces the diff-amp to an
effective CS-stage with half the
load resistance and twice the
W/L-ratio of the pull-down
transistor. The common mode
gain results in
Acm
RD / 2
1
RSS
W
2 2 n Cox I d
L
For a zero common mode gain Rss has to be infinity
ideal current source at the bottom!
Prof. Dr. Hoppe
CMOS Analog Design
242
Real Differential Amplifier
• Real Differential Amplifier amplifies a differential signal and outputs
a single ended voltage Vout
+
Vin1
Vin2
Vout
VSS
Quite often we have a symmetrical voltage range around 0V
e.g. VDD=2.5V, VSS=-2.5V
Then all voltages are referenced to analog ground: 0V
Prof. Dr. Hoppe
CMOS Analog Design
243
Differential to Single Ended
• Just drop one output voltage say Vout1?
Vout
M1
I1
M2
I SS I
2
2
I2
I SS I
2
2
M3
ISS
If we do so, only I/2 = (I2 –I1)/2 is utilised to produce the
output voltage using the voltage drop over RD
Gain is reduced by 50%, as current of M1 is not considered!
Prof. Dr. Hoppe
CMOS Analog Design
244
Differential to Single Ended
• Better solution is to mirror current in M1 into the output path
M3
M4
M1
Vout
M2
M5
ISS
If Vin grows then I1 + I and I2 - I but I3 and I4 grow due to
mirror-effect by I !
I2 gets smaller and I4 grows Vout I !
Prof. Dr. Hoppe
CMOS Analog Design
245
Gain Calculation
• Source-coupled pair M1 and M2 with a current mirror current source
(M3 and M4)
ID2
ID1
M1
M2
VG2
VG1
IBias
MB
VGS2
VGS1
M5
VBulk
Note that M1 and M2 are effected by the substrate bias effect!
Hence bulk-terminals of these transistors may be connecte either
to VSS or to a floating well! MB is the mirror-transistor for
adjustment of the bias-voltage for M5
Prof. Dr. Hoppe
CMOS Analog Design
246
Gain Calculation
• The input differential voltage vID maybe expressed by the differences
in the Gate-Source-Voltages of M1 and M2
ID2
ID1
M1
VG1
M2
VG2
IBias
MB
vID vGS 1 vGS 2
VGS2
VGS1
2iD1
2iD 2
W
W
K 'N
K 'N
L
L
M4
VBulk
The current Iss in M4 is the sum of the currents of M1 and M2
I SS iD1 iD 2
Prof. Dr. Hoppe
CMOS Analog Design
247
Gain Calculation
• The drain currents of M1 and M2 are readily obtained by using both
equations for vID and ISS and by some algebraic transformations:
I
I
iD1 SS SS
2
2
2
W v ID 2
W v ID 4
K 'N
K 'N
2
L
I
L
4
I
SS
SS
I
I
SS SS
2
2
2
W v ID 2
W v ID 4
K 'N
K 'N
L
I
L 4 I SS 2
SS
iD 2
The normalized currents look like
-2
ID/ISS
iD2
2
iD1
vID{ISS/KN’(W/L)}-1/2
Prof. Dr. Hoppe
CMOS Analog Design
248
Gain Calculation
The current equations apply as long as the arguments of the
square roots remain real, imposing the condition:
v ID 2
I SS
K 'N W
L
From the currents one may obtain the transconductances of the
differetial inputs, which have the same magnitude but different signs:
The maximum gain is achieved at vID = 0
gm
I D1
W I SS
(VID 0) K ' N
vID
L 4
Compared with the transconductance of an NMOS-Transistor ID=ISS/2 one sees
that the transconductance is reduced to 50%, because only half of the differential
input voltage is acting at each input node.
Prof. Dr. Hoppe
CMOS Analog Design
249
Gain with current mirror loads
If a current mirror and no load resistances are utilized, the current
mirror mirrors the current in transistor M1 into the path with
transistor M2 with the correct sign and transform the output
differential voltage into a single ended signal.
VDD
M3
M4
iOUT
iD3
iD4
M1
vG1
M2
iD1
iD2
vG2
vOUT
NMOS-inputs
PMOS Current
Mirror load
M5
VBIAS
ISS
Prof. Dr. Hoppe
CMOS Analog Design
250
Gain with current mirror loads
iout is the differential current i1-i2 (perfect matching of devices). The
transconductance of this current is denoted gmd
gmd
iout
W
(VID 0) K ' N 1 I SS 2 gm
vID
L1
Compared with the transconductance of an NMOS-Transistor ID=ISS/2
one sees that the transconductance is now 100%.
Large signal voltage transfer curve:
VDD
M4 linear
M4 Sättigung
VIC
M2 Sättigung
M2 linear
VSS
Prof. Dr. Hoppe
0
CMOS Analog Design
vID
251
Gain with current mirror loads
The (small signal) gain maybe obtained from
iout g md v ID
v ID rout iout
The output resistance is determined by the devices M2 and M4 in the
output sidebranch
rout
1
1
gds 2 gds 4 ( ) I SS
2
4
2
Hence we obtain
A
Prof. Dr. Hoppe
vout
2
W 1
K 'N 1
vID 2 4
L1 I SS
CMOS Analog Design
252
Input Voltage Range
The differential amplifier operates properly until the input voltages are
such that one transistor leaves saturation.
This voltage range is investigated by setting the differential voltage to
zero and sweeping the common mode voltage VIC
To keep M1 (or M2) in saturation. We have to find the highest
(lowest) input voltage keeping M1 (and M2) in saturation:
D1
VDS1 VGS1 – VT1
G1
VDS1
S1
VGS1
VIC (max) VG1 (max) VDD VSG 3 VDS1 VGS1
VDD VSG 3 VTN 1
Voltage drop in M3: VD1
The minimum voltage is determined by the voltage drop in the
source transistor M5
VIC (min) VSS VDS 5 ( sat ) VGS1
Prof. Dr. Hoppe
CMOS Analog Design
253
Slew Rate
The Slew Rate (SR) specifies the speed for charging or
discharging a capacitive load at the output CL to a voltage
which is the gain multiplied with VID. Note that all internal
parasitics contribute to the total output load. The
charging/discharging current is sourced from the current
sink (transistor M5).
SR I 5 / CL
Current in M5
Prof. Dr. Hoppe
CMOS Analog Design
254
3dB-frequency and power dissipation
The 3dB-frequency is determined by the RC-time-constant
of the output branch
3dB 2 f 3dB
1
Rout CL
Power dissipation Pdiss is obtained from the current
supplied or sourced from the bottom-transistor M5 multiplied
with the voltage drop from VDD to VSS
Pdiss (VDD VSS ) I SS
Prof. Dr. Hoppe
CMOS Analog Design
255
Summary of the relevant formula
For a design we use the following fomulas:
Rout
2
( N P ) I 5
Adiff g m1 Rout 2nCox
g md
W1
I d 1 Rout
L1
g ds 2 g ds 4
Pdiss (VDD VSS ) I 5 (VDD VSS ) ( I 3 I 4 )
3dB
1
Rout CL
VIC (min) VSS VDS 5 ( sat ) VGS 2
VIC (max) VDD VSG 3 VDS 1 VGS 1 VDD VSG 3 VTN 1
Prof. Dr. Hoppe
CMOS Analog Design
256
How to meet the design targets?
Assume we have the following specification and we use the 0.8µm
sample technology
VDD VSS 2,5V
SR 10V / µs
f 3dB 100kHz (CL 5 pF )
1,5V ICMR 2V
Adiff 100
Pdiss 1mW
In which order we have to determine the transistor dimensions for
a differential amplifier with NMOS-inputs and a PMOS current
mirror load?
Prof. Dr. Hoppe
CMOS Analog Design
257
0.8µm CMOS Sample Technology
Prof. Dr. Hoppe
CMOS Analog Design
258
Design procedure: I5
The first quantity to be dimensioned is the current of
transistor M5 the source coupling current sink. This
transistor has to provide the current for charging and
dischargig the load capacitance. Hence the Slew-RateSpecification has to be considered:
SR I 5 / CL I 5 / 5 pF 10V / µs
I 5 50µA
Prof. Dr. Hoppe
CMOS Analog Design
259
Design procedure: I5
We have to consider the upper bound for the power
dissipation, which limits I5 to 200µA and we have to be
aware that the this current is relevant for the output
resistance Rout, which itself enters together with CL into the
3dB-frequency, which was specified to exceed 100kHz
Rout has to be less than 318 k
3dB 2 f 3dB
6, 28 100kHz
Rout
Prof. Dr. Hoppe
1
Rout CL
1
Rout 318k
Rout 5 pF
2
318k
N P I 5
CMOS Analog Design
260
Design procedure: I5 then M3(=M4)
Using the channel length modulation factors we obtain I5 = 70µA.
To achieve some design margin we set I5 = 100µA
M3 (and M4) have to dimensioned according to the Input
Common Range ICMR
VIC (max) VDD VSG3 VDS1 VGS1 VDD VSG3 VTN 1
Solving for VGS3 we obtain 2,5V – 2V + 0,7V = 1,2V = VSG3 This
voltage detremines the saturation current of M3, which has to be in
the operating point (vID = 0) equal to Iss / 2 = 50 µA. If use the
equation for the saturation current of M3 and solve for VGS3 = - VSG3
we get
Prof. Dr. Hoppe
CMOS Analog Design
261
Design procedure: I5 then M3(=M4)
Note that M3 is PMOS!
I D3
W
1
50 µA / V 2 3 (VGS 3 VTP ) 2
2
L3
50 µA
W
1
50 µA / V 2 3 (1, 2 0, 7) 2
2
L3
VSG3 1,2V
2 50µA L3
0,7V
50µA / V ² W3
0,5V 2
L3
W3
W3 W4
2
8
L3 L4 0.5²
Prof. Dr. Hoppe
CMOS Analog Design
262
Design procedure: M1 (=M2)
Using the gain specification and using
A
vout
g md
2
vID g ds 2 g ds 4 2 4
g md g m1 g m 2 2 K N ' I D1
K 'N
W1 1
L1 I SS
W1
W
K N ' I SS 1
L1
L1
g ds 2 g ds 4 (N P ) I D1,2 (N P )( I SS / 2)
2 µnC Ox
W1
L1
(N P ) I SS
2 110
W1
µA
L1 V ²
(0, 04 0, 05) 100 µA
23,31
W1
L1
100V / V
100 23.31
Prof. Dr. Hoppe
CMOS Analog Design
W3
L3
W1 W2
18, 4
L1 L2
263
Design procedure: M5
Using the lower ICMR specification we may calculate VDS5
VIC (min) VSS VDS 5 ( sat ) VGS 2
At first we need VGS2 which can be calculated from the current in M2 which is in
the operating point ISS/2=50µA
I2
µnCox W2
2
V
V
GS 2 TN
2 L2
W2/L2 = 18,4 and hence (using VT and the other technology dependent
parameters): VGS2 = 0.222V + 0,7V.
The resulting voltage VDS5(sat) = 0,3V – 0,222V = 0.0777V.
M5 has to provide for this small overdrive voltage of 0.0777V 100µA
W5
2 I5
200µA
300
2
L5 µnCoxVds 5 ( sat )² 110µA 0,0777
Prof. Dr. Hoppe
CMOS Analog Design
264
Design procedure: Fine tuning
M5 is very large. To get a smaller M5 we need to increase M1 (and M2). Then
the voltage drop across the input transistors is less and hence VDS5 is
increased and then a smaller M5 is sufficient to provide the required 100µA
Using W1/L1 = W2/L2 = 25 we get W5/L5 = 150, which is sufficient for the resulting
overdrive voltage VDS5(sat) = 0,11V.
Note that the gain is increased by larger input transistors, but this is no
drawback!
In order to reduce the small channel effects we select as a common channel
length 1µm, which is slightly more than the minimum dimension of 0.8µm
W1 = W2 = 25 µm
W3 = W4 = 8 µm
W5 = 150 µm
Prof. Dr. Hoppe
Cross check: Is the gain large enough?
2
A
1 2
K1' W1
2
L1 I SS 1 2
CMOS Analog Design
K1' W1
2
110 25
117
L1 I SS 0,09
100
265
1. Design targets for 0.35µm design
Assume we have the following specification and
we use the 0.35µm sample technology
VDD VSS 1,65V
SR 10V / µs
f 3dB 100kHz (CL 5 pF )
1.1V ICMR 1.3V
0.55V ICMR 2.95V
Adiff 100
Pdiss 1mW
Prof. Dr. Hoppe
CMOS Analog Design
266
2. Design targets for 0.35µm design
Assume we have the following specification and
we use the 0.35µm sample technology
VDD VSS 1, 65V
SR 20V / µs
f 3dB 200kHz (CL 5 pF )
1.1V ICMR 1.3V
W1/L1=164
W3/L3=84
W5/L5=143
R=13,4kOHM
0.55V ICMR 2.95V
Adiff 200
Pdiss 1mW
Prof. Dr. Hoppe
CMOS Analog Design
267
AMS 0,35µm CMOS Technology
AMS CSD 0,35µm CMOS 3,3V Prozess
Parameter
Description
Parameters
NMOS
Unit
PMOS
Vth0
Threshold Voltage VBS = 0
0,5 0,05 -0,65 0,05
V
K’
Transconductance
175 10% 60 10%
µA/V2
Substrate Bias
0,58
V1/2
Channel Length Modulation
0,06L=1µm 0,06 L=1µm
0,04L=2µm 0,04 L=2µm
V-1
2F
Fermi Potential
0,8
V
0,42
0,8
*Level 1 SPICE Modell CSD 0,35
.MODEL MOSN NMOS VTO=0.5 KP=175U GAMMA=0.58 LAMBDA=0.06 PHI= 0.8
.MODEL MOSP PMOS VTO=-0.65 KP=60U GAMMA=0.42 LAMBDA=0.06 PHI=0.8
Prof. Dr. Hoppe
CMOS Analog Design
268
Transistor Geometries for 0.35µm design
Design No. 1
VDD
M3 2 2 1 1 MODP W = 62U L = 1U
M4 3 2 1 1 MODP W = 62U L = 1U
M1 2 1P 5 0 MODN W = 30U L = 1U
M2 3 1M 5 0 MODN W = 30U L = 1U
M5 5 7 0 0 MODN W = 120U L = 1U
M6 7 7 0 0 MODN W = 120U L = 1U
RR 1 7 18000
M3
M4
iOUT
iD3
iD4
M1
RR
vG1
M7
M2
iD1
iD2
vG2 vOUT
VBIAS M5
ISS
Prof. Dr. Hoppe
CMOS Analog Design
269
Simulations for 0.35µm design
Offset and transfer characteristics
VIN+ 1P 0 DC 1.65
VDD 1 0 DC 3.3
VIN- 1M 0 DC 1.65
CL 3 0 5P
M3 2 2 1 1 MODP W = 62U L = 1U
M4 3 2 1 1 MODP W = 62U L = 1U
M1 2 1P 5 0 MODN W = 30U L = 1U
M2 3 1M 5 0 MODN W = 30U L = 1U
M5 5 7 0 0 MODN W = 120U L = 1U
M6 7 7 0 0 MODN W = 120U L = 1U
RR 1 7 18000
.MODEL MODP PMOS LEVEL=49
.MODEL MODN NMOS LEVEL=49
.DC VIN+ 0.0 3.3 50U
.PRINT DC V(3)
.END
Prof. Dr. Hoppe
CMOS Analog Design
270
Simulations for 0.35µm design
Offset and transfer characteristics
Prof. Dr. Hoppe
CMOS Analog Design
271
Simulations for 0.35µm design
ICMR with unity gain configuration
VIN+ 1P 0 DC 1.65
VDD 1 0 DC 3.3
CL 3 0 5P
M3 2 2 1 1 MODP W = 62U L = 1U
M4 1M 2 1 1 MODP W = 62U L = 1U
M1 2 1P 5 0 MODN W = 30U L = 1U
M2 1M 1M 5 0 MODN W = 30U L = 1U
M5 5 7 0 0 MODN W = 120U L = 1U
M6 7 7 0 0 MODN W = 120U L = 1U
RR 1 7 18000
.MODEL MODP PMOS LEVEL=49
.MODEL MODN NMOS LEVEL=49
.DC VIN+ 0.0 3.3 50U
.PRINT DC V(1M)
.END
Prof. Dr. Hoppe
CMOS Analog Design
VIN+
272
Simulations for 0.35µm design
ICMR with unity gain configuration
Prof. Dr. Hoppe
CMOS Analog Design
273
Simulations for 0.35µm design
Bode Plot
VIN+ 1P 0 DC 1.65 AC 1.0
VDD 1 0 DC 3.3
VIN- 1M 0 DC 1.65
CL 3 0 5P
M3 2 2 1 1 MODP W = 19U L = 1U
M4 3 2 1 1 MODP W = 19U L = 1U
M1 2 1P 5 0 MODN W = 28U L = 1U
M2 3 1M 5 0 MODN W = 28U L = 1U
M5 5 7 0 0 MODN W = 110U L = 1U
M6 7 7 0 0 MODN W = 110U L = 1U
RR 1 7 19000
.MODEL MODP PMOS LEVEL=49
.MODEL MODN NMOS LEVEL=49
.AC DEC 50 1 10MEG
.PRINT AC V(3)
.END
Prof. Dr. Hoppe
CMOS Analog Design
274
Simulations for 0.35µm design
Bode Plot
ADIFF = 43dB
3dB
Frequ.
200kHz
Prof. Dr. Hoppe
CMOS Analog Design
275
Simulations for 0.35µm design
Step Response for Slew-Rate unity gain configuration
VIN+ 1P 0 PWL (0.0 1.0, 1.0U 1.0, 1.00001U 2.0, 3.0U 2.0, 3.00001U, 1.0)
VDD 1 0 DC 3.3
CL 1m 0 5P
M3 2 2 1 1 MODP W = 62U L = 1U
M4 1M 2 1 1 MODP W = 62U L = 1U
M1 2 1P 5 0 MODN W = 30U L = 1U
M2 1M 1M 5 0 MODN W = 30U L = 1U
M5 5 7 0 0 MODN W = 120U L = 1U
M6 7 7 0 0 MODN W = 120U L = 1U
RR 1 7 18000
.MODEL MODP PMOS LEVEL=49
.MODEL MODN NMOS LEVEL=49
.TRAN 0 5U
.PRINT TRAN V(1P) V(1M)
.END
Prof. Dr. Hoppe
CMOS Analog Design
276
Simulations for 0.35µm design
Step Response for Slew-Rate
0.02µs
SR=1V/0.025µs
0.03µs
Prof. Dr. Hoppe
CMOS Analog Design
277
Operational Amplifiers
Prof. Dr. Hoppe
CMOS Analog Design
278
Overview
Operational Transconductance Amplifier – OTA
= Unbuffered Operational Amplifier
1. Design Methodology
2. Two-Stage Opamps
3. Frequency Compensation of Opamps
4. Cascode Opamps
5. Characterization of Opamps
Prof. Dr. Hoppe
CMOS Analog Design
279
Opamp Design Methodology
• Differential-transconductance OTA-stage provides the
differential-to-single-ended conversion as well as good
part of overall gain
⇒ improves noise + offset performance
• Second gain-stage is usually an inverter
• If opamp is to drive low-resistive loads, a buffer (output)
stage must be included ⇒ to lower the output
resistance and maintain a large signal swing
• Bias circuit provides the proper operating point to each
stage
Prof. Dr. Hoppe
CMOS Analog Design
280
Opamp Design Methodology
• Compensation is necessary to ensure
close-loop stability!
Prof. Dr. Hoppe
CMOS Analog Design
281
Opamp Design Methodology
Ideally, an opamp has:
•
•
•
•
•
•
Infinite differential-voltage gain
Infinite input-resistance
Zero output-resistance
Infinite bandwidth
Perfect rejection of common-mode voltage (CMRR →∞)
Perfect rejection of supply voltage variations (PSRR
→∞)
In reality, an opamp only approaches these
conditions:
For most applications involving unbuffered opamps,
an open-loop of 5000 or more is usually sufficient
Prof. Dr. Hoppe
CMOS Analog Design
282
Ideal and non ideal Opamp
Symbol for an opamp realized by a VCVS
Prof. Dr. Hoppe
CMOS Analog Design
283
Ideal and non ideal Opamp
Model for a real Opamp
Prof. Dr. Hoppe
CMOS Analog Design
284
Ideal and non ideal Opamp
Modelparameters for Opamp-Model
•
Rid, Cid : differential-input impedance
•
Ricm : common-mode input resistance
•
Rout: output resistance
•
VOS: input-referred offset voltage ( necessary to make Vo=0 when both
inputs are grounded)
•
IB1, IB2: input-bias current (approx. zero for a CMOS opamp)
•
Vi/CMRR : represents the effect of a finite common-mode rejection ratio on
the opamp output.
•
en2 and in2 : model the input-referred noise generated by the opamp
components. These are voltage- and current-noise spectral densities, with
units of mean square volts and mean square amperes, respectively. They
have no polarity and are always assumed to add.
Prof. Dr. Hoppe
CMOS Analog Design
285
OpAmp non-idealities
a) Finite Bandwidth:
Prof. Dr. Hoppe
CMOS Analog Design
286
Finite Bandwidth
p1, p2, p3 … are poles of the opamp open-loop transfer
function.
In general, pi = -ωi , where ωi is the reciprocal timeconstant or break-frequency of the pole pi.
Zeros are ignored at the present time as they appear
frequencies well-above the unity gain frequency of the
opamps to be discussed.
Prof. Dr. Hoppe
CMOS Analog Design
287
Finite Bandwidth
Bode-Diagram: Amplification vs. Frequency (semilog.)
Prof. Dr. Hoppe
CMOS Analog Design
288
Finite Bandwidth and PSSR
• Typical frequency response: imposed by design, ω1 is
much lower than other pole frequencies
• ⇒ω1has the dominant influence in the frequency
response (p1 is the dominant pole)
b) Finite PSSR (Power Supply Rejection Ratio)
• PSRR : represents the change in the output voltage
caused by a variation on the supply
• voltage. PSRR+ and PSRR- are referred to VDD and
VSS, respectively.
Prof. Dr. Hoppe
CMOS Analog Design
289
Finite PSSR
• Fully-differential (differential-in, differential-out)
structures minimize the effect of supply variations on the
opamp output, as they are seen as common-mode
voltages, at expense of higher circuitry complexity,
however.
Prof. Dr. Hoppe
CMOS Analog Design
290
OpAmp non-idealities
c) finite Slew-Rate
• The opamp output has a limited capability to
drive/source load currents. There’s a limited range over
which the output voltage can swing while still maintaining
high-gain property.
• The limiting voltage-rate associated to the output swing
when a large-signal is applied to the input is called slewrate, which is usually determined by the maximum
current available to charge/discharge a capacitance.
Prof. Dr. Hoppe
CMOS Analog Design
291
Slew Rate
Slewing effect on a unity-gain closed-loop opamp configuration. Normally, slew-rate is determined by the first
stage, rather than by the output circuit.
Prof. Dr. Hoppe
CMOS Analog Design
292
OpAmp non-idealities
d) finite Settling Time
• Important in sampled-data applications, it is the time
needed for the opamp output to reach a final value, to
within a predetermined tolerance, following a smallsignal applied to the input.
• The settling time can be completely determined from the
location of poles (and zeros) in the opamp small-signal
transfer function
Prof. Dr. Hoppe
CMOS Analog Design
293
Settling Time
Time-response to a small-signal voltage-step on
closed-loop configuration (buffer)
Prof. Dr. Hoppe
CMOS Analog Design
294
Typical Unbuffered CMOS Opamp
Specifications
•
•
•
•
•
•
•
•
•
•
•
•
Open-loop Voltage Gain
GBW (unity-gain frequency)
Settling-time
Slew-rate
Input CMR
CMRR
PSRR
Output swing
Output resistance
Offset voltage
Noise
Layout area
Prof. Dr. Hoppe
≥ 70dB
≥ 2MHz
≤ 1μs
≥ 2V/μs
≥ ± 3V
≥ 60dB
≥ 60dB
≥ ± 4V
≤ 50 – 100Ω
≤ 10mV
≤ 100nV/Hz1/2 @ 1KHz
≤ 120k sq μm
CMOS Analog Design
295
Typical Unbuffered CMOS Opamp
Specifications
Boundary Conditions
Supply-voltage: ±5V ±10%
Supply-current: 100μA (quiescent)
Temperature range: 0 to 70°C
Prof. Dr. Hoppe
CMOS Analog Design
296
Typical Unbuffered CMOS Opamp:
2 Stage Architecture
M1 to M5 stage 1, M6 and M7 stage 2
Compensation
Capacitor CC
Prof. Dr. Hoppe
CMOS Analog Design
297
Frequency-Compensation of Opamps
Opamps are primarily used in closed-loop configuration.
The high and imprecise gain can be used with
negative feedback to achieve a very accurate transfer
function, which approximately depends only on the
feedback elements.
Prof. Dr. Hoppe
CMOS Analog Design
298
Negative Feedback System
If F(s)A(s) = -1 at s = j1 the gain reaches infinity
and the circuit amplifies ist own noise until it
begins to oscillate. In other words:
if F(j1 )A(j1 ) = -1 the circuit begins to oscillate!
Barkhausen criteria
Prof. Dr. Hoppe
CMOS Analog Design
299
Negative Feedback System
This situation happens at a particular ferquency s = j1 ,
where magnitude and phase
F(s)A(s) = 1 and arg{F(s)A(s)} = -180
represent F(j1 )A(j1 ) = -1
Note that total phase shift around the loop at critical
frequency 1 is 360 (or 0 because of mod(360°feature) but the negative feedback alone adds 180 of
phase shift, so we have 180 (or -180) left for the
OpAmp and the feedback circuit.
Loop gain of unity or larger is also required to enhance the
oscillation amplitude!
Prof. Dr. Hoppe
CMOS Analog Design
300
Negative Feedback System
The frequencies where the magnitude and the
phase of the loop gain are equal to unity or 180 are of special importance to stability.
For stability one has to avoid the Barkhausen
criteria by adding appropriate passive
components into the loop!
How to do so?
Look at the Bode-Diagram!
Prof. Dr. Hoppe
CMOS Analog Design
301
Frequency-Compensation of Opamps
It’s imperative that the signal fed back to the input be of
such amplitude and phase that it does not regenerate
the signal around the loop, leading to either an
oscillation or clamping the opamp output to one of the
supply potentials.
In order to avoid positive and regenerative feedback,
the following conditions should be met (in an negative
feedback system):
Loop Gain = - F(s)A(s) < 1 and Phaseshift < -180
Prof. Dr. Hoppe
CMOS Analog Design
302
Example for Bode Plots
Look at a transfer function:
H ( s ) 100
s 1
1 1/ s
0.1
( s 10)( s 100)
(1 s /10)(1 s /100)
All poles and roots are given in the form: (1+s/k)
One root at s = -1 and two poles at s = -10 and s = -100.
For a Bode-Plot the complex factors are written as phasors,
i.e. absolute value times the phase factor.
H ( s) 0.1
1 j /1 (1 j )
1 s /1
0.1 (0.1)
(1 s /10)(1 s /100)
(1 j /10) (1 j /100) (1 j /10)(1 j /100)
(1 j ) exp(arctan( j /1))
Prof. Dr. Hoppe
CMOS Analog Design
303
What looks the Bode Plot like?
MATLAB generates the Bode-Plot using the commands
– >> Mysys=tf(100*[1 1],[1 110 1000])
–
– Transfer function:
magnitude
– 100 s + 100
– -----------------– s^2 + 110 s + 1000
–
phase
– >> bode(Mysys)
Bode diagram consists of 2
plots: magnitude (or „gain“) in
dB and phase (linear) against
the logarithmic frequency
Prof. Dr. Hoppe
CMOS Analog Design
304
Asymptotic Bode Plots: The Phase
Note: Phase factor is exponential of the arctangens of the fraction of
imaginary part divided by the real part of the complex number.
Hence the total phase is the sum of the individual phase angles.
The real coefficient which is multiplied with the fraction (here 0.1) in
general maybe positive or negative:
A positive factor has phase 0 and a negative factor -180
H ( s) H ( s) exp j(arctan(0) exp j(arctan() exp j( arctan( /10) exp j( arctan( j /100)
H ( s) exp(exp j(arctan(0 j j /10 /100)
Drawing the phase is simple, just draw the phase-angles individually
and add them!
Prof. Dr. Hoppe
CMOS Analog Design
305
Asymptotic Bode Plots: The
Magnitude
Magnitude is a product of different terms. In order to draw them in a
simple fashion, we take a logarithm.
To be specific we write the magnitude in units of decibels.
Each quantity Q has a representation X in decibels:
X = 20.0log10(Q)
The magnitude in decibels reads:
H ( s ) 0.1
1 j /1
(1 j /10) (1 j /100)
20 log H ( s) 20 log 0.1 20 log 1 j /1 20 log 1 j /10 20 log 1 j /100
Changing to decibels transforms the multiplication into a summation
of constant terms and terms of the form 20log101+j/k!
Prof. Dr. Hoppe
CMOS Analog Design
306
Constructing a Bode Diagram
A constant term:
H(s)=100=40dB
The magnitude is straight line and the phase is 0
Prof. Dr. Hoppe
CMOS Analog Design
307
Constructing a Bode Diagram
A real pole:
1
H ( s)
1
s
1
0
1 j
0
0 is the -3dB or corner frequency.
The magnitude is given by
20 log10 H ( s ) 20 log10
1
1 j
0
20 log10
1
0
2
Boundary Cases
low frequency 0 : H ( s ) 0dB
2
high frequency 0 : H ( s ) 20 log10
20 log10
0
0
break frequency 0 : H ( s ) 20 log10
0
1 20 log10
0
2
Prof. Dr. Hoppe
CMOS Analog Design
2 3.01dB
308
Constructing a Bode Diagram
1
A real pole: H ( s)
1
s
0
1
1 j
0
0 is the -3dB or corner frequency.
The phase is given by
H ( s ) arctan
0
Boundary Cases
low frequency 0 : H ( s ) arctan 0 0
high frequency 0 : H ( s ) arctan 90
break frequency 0 : H ( s ) arctan 1 45
Prof. Dr. Hoppe
CMOS Analog Design
2
4
rad
rad
309
Constructing the Magnitude
Using the high and low frequency approximation we
obtain:
Prof. Dr. Hoppe
CMOS Analog Design
310
Constructing the Phase
Using the high and low frequency approximation we
obtain:
Prof. Dr. Hoppe
CMOS Analog Design
311
Constructing a Bode Diagram
A real zero:
H ( s) 1
s
0
1 j
0
The magnitude is given by
20log10 H ( s ) 20log10 1 j
1
0
20log10
0
2
Boundary Cases
low frequency 0 : H ( s ) 0dB
2
high frequency 0 : H ( s ) 20log10 20log10
0
0
2
break frequency 0 : H ( s ) 20log10
Prof. Dr. Hoppe
0
1 20log10
0
CMOS Analog Design
2 3.01dB
312
Constructing a Bode Diagram
A real zero:
H ( s) 1
s
0
1 j
0
The phase is given by
H ( s ) arctan
0
Boundary Cases
low frequency 0 : H ( s ) arctan 0 0
high frequency 0 : H ( s ) arctan 90
break frequency 0 : H ( s ) arctan 1 45
Prof. Dr. Hoppe
CMOS Analog Design
2
4
rad
rad
313
Constructing a Bode Diagram
Example for neg. real
zero:
s
H ( s) 1
30
Magnitude rises by
20dB per decade
Phase rises by 90
10% of 0
10 times 0
Prof. Dr. Hoppe
CMOS Analog Design
314
Constructing a Bode Diagram
Example for positive
real zero
H ( s) 1
s
30
Decreases phase
margin! Like a pole!
Prof. Dr. Hoppe
CMOS Analog Design
315
Rules for Ass. Bode Plots
Bode Plots illustrate the asymptotic behavior of
magnitude and phase of a complex function in terms
of it‘s poles and zeros.
Rule 1: The slope of the magnitude plot changes by
+20dB/dec at every zero and by -20dB/dec at every
pole frequency.
Rule 2: At every pole(zero) frequency m the phase
begins to fall(rise) at approximately 0.1m,
experiences a change of -45(+45) at m and 90(+90) at 10 m
Note that the phase is much more affected by high
frequency poles than the magnitude is!
Prof. Dr. Hoppe
CMOS Analog Design
316
Location of poles
Poles and zeros in the complex plane: sp = jp + p
Pole in the RHP: p > 0. As the impulse response
includes a term of the form exp(jp + p)t then the
time domain response contains a growing exponential
oscillation
Pole at the imaginary axis: p = 0. In the time domain
response circuit sustains oscillation
Pole in the LHP: p < 0. As the impulse response
includes a term of the form exp(jp + p)t then the
time domain response contains a falling exponential
oscillation is damped out!
If one plots the location of poles as the loop gain varies
one gets a root locus diagram
Prof. Dr. Hoppe
CMOS Analog Design
317
Frequency-Compensation of Opamps
Stability is achieved if following condition hold
– Stability condition is better illustrated with the use of Bode
diagrams. The A(jω)F(jω) curve must cross the 0dBpoint before Arg[- A(jω)F(jω)] reaches 0°
– A measure of stability is given by the phase value when
A(jω)F(jω) =1 and it is called phase-margin M.
Prof. Dr. Hoppe
CMOS Analog Design
318
Frequency-Compensation of Opamps
Note: CMOS OpAmp has a negative
feedback: Inherent phase margin of 180
Prof. Dr. Hoppe
CMOS Analog Design
319
Frequency-Compensation of Opamps
The importance of good stability with adequate
phase-margin (ΦM) is better understood by
considering the response of the closed-loop system
in time domain, shown in the figure below, for
different phase-margin values.
• Larger phase-margins result in less ringing of the
output signal.
• It’s desirable to have ΦM of at least 45°, whereas
60° is preferable in most cases.
Prof. Dr. Hoppe
CMOS Analog Design
320
Frequency-Compensation of Opamps
Closed-loop time-response for different ΦM values
Prof. Dr. Hoppe
CMOS Analog Design
321
Frequency-Compensation of Opamps
2-stage opamp equivalent small-signal circuit
There are two poles (second order system)
Prof. Dr. Hoppe
CMOS Analog Design
322
Frequency-Compensation of Opamps
There are two poles (second order system)
Prof. Dr. Hoppe
CMOS Analog Design
323
Frequency-Compensation of Opamps
As Ro1 and Ro2 and naturally high in order to obtain
very high voltage gain on every stage, both poles
have relatively low-frequencies ⇒ very low ΦM ⇒
frequency compensation is needed to move one
pole to higher frequencies.
Prof. Dr. Hoppe
CMOS Analog Design
324
The Miller-Capacitance (pole-splitting)
Compensation of Opamps
This technique comprises connecting a capacitor CC from
the output to the input of the second stage, leading to:
i) the effective capacitance Co1 is increased by a factor
(gm2Ro2) CC , which moves down p1 quite considerably.
ii) owing to the negative feedback, the second-stage output
resistance is reduced, moving p2 to higher frequencies
Prof. Dr. Hoppe
CMOS Analog Design
325
The Miller-Capacitance (pole-splitting)
Compensation of Opamps
This technique comprises connecting a capacitor CC from
the output to the input of the second stage, leading to:
Prof. Dr. Hoppe
CMOS Analog Design
326
The Miller-Capacitance (pole-splitting)
Compensation of Opamps
Prof. Dr. Hoppe
CMOS Analog Design
327
The Miller-Capacitance (pole-splitting)
Compensation of Opamps
⇒ as far as phase-shift is concerned, a RHP zero behaves
like a LHP pole ⇒ΦM is degraded
⇒ Compensation comprises moving p2 and z1 (except
p1) to frequencies sufficiently high beyond the unitygain frequency of the opamp
⇒
a first-order system condition is approached
Prof. Dr. Hoppe
CMOS Analog Design
328
The Miller-Capacitance (pole-splitting)
Prof. Dr. Hoppe
CMOS Analog Design
329
The Miller-Capacitance (pole-splitting)
Compensation of Opamps
Root-locus movement as CC increases and Bode plots before and after
compensation for gain and Bode plot after compensation for phase.
ArgA(jF(j A(jF(j
unkorrigiert
104dB
0dB
180
6dB/Okt.
p’1
12dB/Okt.
p1
p’2
p2
90
M
0
j
p2
Prof. Dr. Hoppe
p’2
p’1
p1
CMOS Analog Design
z1
330
Eliminate or Relocate the RHP zero
The RHP zero can be displaced by inserting a nulling
resistor RZ in series with CC
Prof. Dr. Hoppe
CMOS Analog Design
331
Eliminate or Relocate the RHP
zero
Again, assuming that p1 and p2 are widely spaced
and Rz << Ro1 or Ro2, it turns out
Prof. Dr. Hoppe
CMOS Analog Design
332
Eliminate or Relocate the RHP
zero
Prof. Dr. Hoppe
CMOS Analog Design
333
Eliminate or Relocate the RHP
zero
Prof. Dr. Hoppe
CMOS Analog Design
334
Eliminate or Relocate the RHP
zero
Implementation of Resistor by linear MOSFET
Prof. Dr. Hoppe
CMOS Analog Design
335
Design procedure
Specification
A > 5000 V/V
VDD = 2,5
VSS = -2,5V
Verst.*Bandbr.
(GB): 5 MHz
CL = 10 pF
Slew Rate >
10V/µs
Vout-Bereich: 2V ICMR = -1 bis 2V
Prof. Dr. Hoppe
CMOS Analog Design
Pdiss 2mW
336
Design procedure
Circuit diagram
M3
IREF
M6
M4
Io
R
CC
Vout
CL
vin
M1
M2
+
+
-
Prof. Dr. Hoppe
M5
M7
CMOS Analog Design
337
1. Choice of technology and
channel length
⇒ Compensation comprises moving p2 and z1 (except
p1) to frequencies sufficiently high beyond the unitygain frequency (the Gain-Bandwidth GBW) of the
opamp
⇒
a first-order system condition is approached
Prof. Dr. Hoppe
CMOS Analog Design
338
AMS 0,35µm CMOS Technology
AMS CSD 0,35µm CMOS 3,3V Prozess
Parameter
Description
Parameters
NMOS
Unit
PMOS
Vth0
Threshold Voltage VBS = 0
0,5 0,05 -0,65 0,05
V
K’
Transconductance
175 10% 60 10%
µA/V2
Substrate Bias
0,58
V1/2
ChannelLength Modulation
0,06L=1µm 0,06 L=1µm
0,04L=2µm 0,04 L=2µm
V-1
2F
Fermi Potential
0,8
V
0,42
0,8
*Level 1 SPICE Modell CSD 0,35
.MODEL MOSN NMOS VTO=0.5 KP=175U GAMMA=0.58 LAMBDA=0.06 PHI= 0.8
.MODEL MOSP PMOS VTO=-0.65 KP=60U GAMMA=0.42 LAMBDA=0.06 PHI=0.8
Prof. Dr. Hoppe
CMOS Analog Design
339
0.8µm CMOS Sample Technology
Prof. Dr. Hoppe
CMOS Analog Design
340
1. Choice of technology and
channel length
We use a 0.8µm CMOS technology
⇒ Minimum Channel Length is 1,0µm
Prof. Dr. Hoppe
CMOS Analog Design
341
The Miller Capacitance
Moves p2 and z1 (except p1) to frequencies sufficiently
high beyond the unity-gain frequency (the Gain-Bandwidth
GBW) of the opamp
⇒ OpAmp behaves like a a first-order system
(Low Pass)
Prof. Dr. Hoppe
CMOS Analog Design
342
2. Choose the Miller-Capacitance
As outlined in the previous slides
Position of non dominant pole and the root in RHP are given by
the transconductance of second stage (i.e. that of transistor M6
in the schematic) and the output capacitance (i.e. in principle
the load cap)
p2
gm 6
CL
z1
gm 6
CC
GB is amplification at 0Hz multiplied with p1:
g(1st . sat ) g(2 nd stage. sat ) Ro1R02 A (0)
1
p1
g(2. stage ) Ro1Ro 2CC
Prof. Dr. Hoppe
CMOS Analog Design
g m1
GB
Cc
343
Choosing the Miller-Capacitance
The 2 stage OpAmp has two poles and one RHP-zero. If the zero is assumed
to be placed 10 times higher then the Gain-Bandwidth (GB), then the second
pole has to be placed at a frequency 2.2times higher than GB to obtain a
phase margin of 60 = M
M 180 Arg A( j ) F ( j )
180 tan 1
120 tan 1
p1
tan 1
p2
tan 1
z1
60
GB
GB
GB
tan 1
tan 1
p1
p2
z1
The total phase is the
sum of the individual
phase contributions of
the two poles and the
zero
The phase margin has to be 60 below and above GB. Hence all
frequencies are replaced in the formula by GB.
GB is given by the DC-amplification multiplied by the absolute value of
the dominant pole p1. As A(0) is very large we obtain
Prof. Dr. Hoppe
CMOS Analog Design
344
Choosing the Miller-Capacitance
together with our assumption that the zero is placed 10 times
higher then the Gain-Bandwidth (GB) in the third term we obtain
GB
120 tan A (0) tan
tan 1 0,1
p2
1
24,3 tan 1
1
GB
p2
tan 1 A (0) tan 1 ( ) 90
tan 1 (0.1) 5,7
Therefore the pole p2 has to be located 2.2 times higher then GB:
tan 24,3 tan(tan 1
p2
Prof. Dr. Hoppe
GB
) 0.45
p2
GB
2.2GB
0.45
CMOS Analog Design
345
Choosing the Miller-Capacitance
If the RHP-zero is placed at 10xGBW, by placing the non dominant pole
p2 at a frequency 2.2times higher than GBW gives 60 = M
gm6
g
g
m 6 2.2 m1
CL
CL
CC
g
g
z1 m 6 10GBW 10 m1
CC
CC
p2
g m 6 10 g m1 or g m 6 10 g m 2
with g m 6 10 g m1
g m1
g
2.2 m1 10CC 2.2CL
CL
10CC
CC 0, 22CL
here CL 10 pF
CC 2.2 pF better CC 3 pF
Prof. Dr. Hoppe
CMOS Analog Design
346
Choosing I5 for the Slew Rate
The slew rate is determined by the current of M5 divided by the load
capacitance of the differential stage at the input. The load is the Miller
capacitor:
SR I 5 / CL*) I 5 / 3 pF 10V / µs
I5 SR(Cc ) 10V / µs 3 pF 30µA
*)Load capacitace for I5 is the compensation capacitor!
Prof. Dr. Hoppe
CMOS Analog Design
347
Choosing W3 and W4
These two devices form a current mirror. The relevant spec-value is the
maximum ICMR-voltage Vin(max) = 2.0V:
W3
I5
K VDD Vin (max) VT 03 (max) VT 1 (min)
'
3
30µA
50 10
6
2,5V 2,0V 0,85V 0,55
2
2
15µm
Therefore we have identical widths of 15µm for M3 and M4
Prof. Dr. Hoppe
CMOS Analog Design
348
Choosing gm1 i.e. W1 and W2
gm1 is the transconductance of the input transistors forming a differential pair
(M1 and M2). This quantity is related to the GB specified and Cc obtained
already:
gm1
GB
gm1 5 106 2 3 1012 94, 25µS
Cc
Since M1 and M2 provide 50% of the I5-current which was calculated to be
30µA, we find
g m12
W1 W2
94, 252
2,79 3
L1 L2
2 K N ' I1 2 110 15
Prof. Dr. Hoppe
CMOS Analog Design
349
Choosing W5 by VDS5
The drain-source voltage of M5 is obtained from the required minimum input
common mode voltage -1.0V.
I5
VT 1 (max)
ß1
VDS 5 Vin (min) VSS
1V ( 2,5V )
6
30 10
V 0,85V 0,35V
3 110 106
Note: ß = K‘/W/L)
This voltage must not drop below VDS(sat) in order to keep M5 (as an
effective current source) in saturation
2I5
W5
2I5
VDS 5 ( sat )
'
2
ß5
L5 K 5 (VDS 5 )
2 30 106
6
110 10 (0,35)
Prof. Dr. Hoppe
2
4, 49 4,5
CMOS Analog Design
350
Choosing W6 from gm6 and gm4
Since the transconductances of M1 and M2 are identical we obtain from the
considarations for the choice of the Miller capacitance
gm 6 2, 2
g m 2 CL
g 10 pF
2, 2 m1
942,5µS
Cc
2, 2 pF
gm4 is determined by I5: ID4 = I5/2:
gm 4
W
2 K P ' I D 4 2 50 1012 15 15 150µS
L 4
From gm4, W4/L4 and gm6 we may calculate W6/L6 : Mirroring in first stage
requires VSG4 VSG6 hence:
942
W W gm 6
15
94
150
L 6 L 4 g m 4
Prof. Dr. Hoppe
CMOS Analog Design
351
Choosing W7
The current ratios of M6 and M5 determine the width of this transistor
W W I6 W
14
L 7 L 5 I 5 L 7
I6 can be determined from gm6 and the W/L-ration of this transistor from
the small signal formula of the input transconductance. If M7 leaves
saturation then we are at the minimum output-voltage-range (here -2V):
Vmin (out ) 2,5V VDS 7 ( sat )
VDS 7 ( sat )
2I7
2 95
0,351V
W
110 14
K N' 7
L7
The minimum output voltage is met, hence first cut design is complete!
Prof. Dr. Hoppe
CMOS Analog Design
352
Recheck Gain and Power
With the dimensions obtained so far, we check whether Pdiss and A are OK
Pdiss 5V 30µA 95µA 0,625mW 2mW
2 gm 2 gm 6
A
I 5 (2 7 ) I 6 (6 7 )
2 942,5 92, 45 1012
7696V / V 5000V / V
12
30(0,04 0,05)95(0,04 0,05) 10
First cut design meets specification!
Prof. Dr. Hoppe
CMOS Analog Design
353
Final Design with dimensions
2,5V
M3
15/1
IREF
M6
94/1
M4
15/1
Io
R
vin
+
+
VBIAS
-
CC =3 pF
M1
3/1
M2
3/1
95µA
vout
CL =10 pF
30µA
M7
14/1
M5
4,5/1
-2,5V
Prof. Dr. Hoppe
CMOS Analog Design
354
How to simulate
SPICE-simulations are not straightforward as we have to
design certain test circuits. For DC- and AC-simulation
we use the open-loop configuration.
We have to set one of the inputs to analog ground (i.e.
VDD = 2.5V and VSS = -2,5V). Analog ground Vanagnd is in
the middle (here 0V).
We define the OpAmp as a .subcircuit for convenience
Prof. Dr. Hoppe
CMOS Analog Design
355
How to simulate
DC- and AC-Analysis
1. We have a large DC-amplification, one input (Vin-) is
set to Vanagnd hence the other differtial input (Vin+) is
assumed to change between -5mV and +5mV
2. We expect a 3dB-frequency at 5 MHz so we perfrorm a
decadic frequency sweep at Vin+ and produce a
semilogarithmic gain plot and a linear plot for the phase
margin
Prof. Dr. Hoppe
CMOS Analog Design
356
OpAmp-Subcuircit
.subckt OPAMP 1 2 6 8 9
M1 4 2 3 3 NMOS1 W = 3U L = 1U AD = 18P AS = 18P PD = 18U PS = 18U
M2 5 1 3 3 NMOS1 W = 3U L = 1U AD = 18P AS = 18P PD = 18U PS = 18U
M3 4 4 8 8 PMOS1 W = 15U L = 1U AD = 90P AS = 90P PD = 42U PS = 42U
M4 5 4 8 8 PMOS1 W = 15U L = 1U AD = 90P AS = 90P PD = 42U PS = 42U
M5 3 7 9 9 NMOS1 W = 4.5U L = 1U AD = 27P AS = 27P PD = 21U PS = 21U
M6 6 5 8 8 PMOS1 W = 94U L = 1U AD = 564P AS = 564P PD = 200U PS =
200U
M7 6 7 9 9 NMOS1 W = 14U L = 1U AD = 84P AS = 84P PD = 40U PS = 40U
M8 7 7 9 9 NMOS1 W = 4.5U L = 1U AD = 27P AS = 27P PD = 21U PS = 21U
CC 5 6 3.0P
.MODEL NMOS1 ...............
.MODEL PMOS1 ..........
IBIAS 8 7 30U
.ENDS
Prof. Dr. Hoppe
CMOS Analog Design
357
DC-AC-OpAmp-Simulation
OPEN LOOP CONFIGURATION
VIN+ 1 0 DC 0 AC 1.0
VDD 4 0 DC 2.5
VSS 0 5 DC 2.5
VIN- 2 0 DC 0
CL 3 0 10P
X1 1 2 3 4 5 OPAMP
.OP
.DC VIN+ -0.005 0.005 100U
DC-control statements
.PRINT DC V(3)
.AC DEC 10 1 10MEG
AC-control statements
.PRINT AC VDB(3) VP(3)
.PROBE
.END
Prof. Dr. Hoppe
CMOS Analog Design
358
DC-AC-Results
Output voltage swing and enlargement yields input offset!
Prof. Dr. Hoppe
CMOS Analog Design
359
AC-Results
DC gain is 80dB, AC-gain falls by 20 dB/dec. GB is 5,3MHz,
phase-margin is 65.
Prof. Dr. Hoppe
CMOS Analog Design
360
0.35µm Design:Spec.
A > 10000 V/V
VDD = 1,65 V
VSS = -1,65V
GB: 10 MHz
CL = 10 pF
Slew Rate > 10V/µs
Vout-Range: 1,3V
ICMR = -0.6V…1,2V Pdiss 2mW
Prof. Dr. Hoppe
CMOS Analog Design
361
0.35µm Design: First Cut Hand
Parameter
Value
Cc
3 pF
I5
30µA
W3= W4
41µm
W1= W2
5µm
W5
2,5µm
W6
176µm
W7
5µm
(L=0.7µm)
OpAmp-Design-Parameters 0,35µm
Prof. Dr. Hoppe
CMOS Analog Design
362
DC-Analysis
• Modified First Cut Design to remove offset
Output Voltage Range:
0,7V .. 3.2V
Prof. Dr. Hoppe
CMOS Analog Design
363
0.35µm Design: Offset Free
Parameter
Value
Cc
3 pF
I5
30µA
W3= W4
16µm
W1= W2
7µm
W5
2,5µm
W6
176µm
W7
5µm
(L=0.7µm)
OpAmp-Design-Parameters 0,35µm
Prof. Dr. Hoppe
CMOS Analog Design
364
0.35µm Design
Prof. Dr. Hoppe
CMOS Analog Design
365
AC-Analysis
DC gain is 80dB, AC-gain falls by 20 dB/dec. GB is 5,3MHz,
phase-margin is 65.
Prof. Dr. Hoppe
CMOS Analog Design
366
AC-Results
DC gain is 88dB, AC-gain falls by 20 dB/dec. GB: 10,2MHz,
phase-margin is 61.
Prof. Dr. Hoppe
CMOS Analog Design
367
Unity Gain Configuration
Prof. Dr. Hoppe
CMOS Analog Design
368
Unity-Gain-Results
Input Common Range:
Transfer Curve has slope „1“
M5 sources 30 mA
ICMR: 0,6V .. 3,0V
Prof. Dr. Hoppe
CMOS Analog Design
369
Transient Unity Gain Simulation
• Slew Rate: Rising 11V/µs Falling 5.5V/µs
Prof. Dr. Hoppe
CMOS Analog Design
370
• Falling Slew Rate 10V/µs with Ibias = 70µA
Prof. Dr. Hoppe
CMOS Analog Design
371