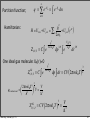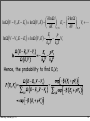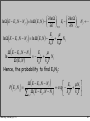Download Introduction Statistical Thermodynamics

Introduction
Statistical Thermodynamics
Monday, January 5, 15
1
Molecular Simulations
◆
Molecular dynamics:
solve equations of
motion
MD
r1
r2
rn
◆
MC
Monte Carlo:
importance sampling
2
Monday, January 5, 15
r1
r2
rn
2
3
Monday, January 5, 15
3
4
Monday, January 5, 15
4
Questions
What is the desired
distribution?
•
How can we prove that this scheme
generates the desired distribution of
configurations?
•
Why make a random selection of the
particle to be displaced?
•
Why do we need to take the old
configuration again?
•
How large should we take: delx?
5
Monday, January 5, 15
5
Outline
Rewrite History
•
Atoms first! Thermodynamics last!
Thermodynamics
•
First law: conservation of energy
•
Second law: in a closed system entropy increase and takes its
maximum value at equilibrium
System at constant temperature and volume
•
Helmholtz free energy decrease and takes its minimum value at
equilibrium
Other ensembles:
•
Constant pressure
•
grand-canonical ensemble
6
Monday, January 5, 15
6
Atoms first
thermodynamics next
Monday, January 5, 15
7
A box of particles
We have given the particles an
intermolecular potential
Newton: equations of motion
F(r) = -ru(r)
d2 r
m 2 = F(r)
dt
Conservation of total energy
Monday, January 5, 15
8
Phase space
Thermodynamics: N,V,E
Molecular:
Γ N = {r1 , r2 ,…, rN , p1 , p 2 ,…, p N }
point in phase space
{p1, p 2 ,…, p N }
Γ N (0)
Why this one?
trajectory: classical mechanics
Γ N (t )
{r1, r2 ,…, rN }
Monday, January 5, 15
9
All trajectories with the same initial total energy should
describe the same thermodynamic state
{p1, p 2 ,…, p N }
These trajectories define a probability
density in phase space
{r1, r2 ,…, rN }
Monday, January 5, 15
10
Intermezzo 1: phase rule
•
Question: explain the phase rule?
•
Phase rule: F=2-P+C
•
F: degrees of freedom
•
P: number of phases
•
C: number of components
•
Monday, January 5, 15
Why the 2?
11
Making a gas
What do we need to specify to
fully define a thermodynamic system?
1. Specify the volume V
2. Specify the number of
particles N
3. Give the particles:
initial positions
initial velocities
More we cannot do: Newton takes over!
System will be at constant:
N,V,E
(micro-canonical ensemble)
Monday, January 5, 15
12
Pressure
What is the force I need to apply to
prevent the wall from moving?
How much work I do?
Monday, January 5, 15
13
Collision with a wall
Elastic collisions:
Does the energy change?
What is the force that we
need to apply on the wall?
Monday, January 5, 15
14
Pressure
•
one particle:
2 m vx
•
# particles:
ρ A vx
•
50% is the positive directions: 0.5
•
P A = F = ρ A m v x2
•
Kinetic energy: UK = ½ m v2 = ³⁄₂ kB T
•
•
Monday, January 5, 15
(we define temperature)
Pressure: P V = N kB T
15
Experiment (1)
NVE1
NVE2
E1 > E2
What will the moveable wall do?
Monday, January 5, 15
16
Experiment (2)
NVE2
E1 > E2
NVE1
Now the wall are heavy molecules
What will the moveable wall do?
Monday, January 5, 15
17
Newton + atoms
•
We have a natural formulation of the
first law
•
We have discovered pressure
•
We have discovered another
equilibrium properties related to the
total energy of the system
Monday, January 5, 15
18
Thermodynamics
(classical)
Monday, January 5, 15
19
Experiment
NVE1
NVE2
E1 > E2
The wall can move and exchange energy:
what determines equilibrium ?
Monday, January 5, 15
20
Classical Thermodynamics
•
1st law of Thermodynamics
•
•
2nd law of Thermodynamics
•
Monday, January 5, 15
Energy is conserved
Heat spontaneously flows from hot to
cold
21
Classical Thermodynamics
Carnot: Entropy difference between two
B
states:
dQrev
S = SB
SA =
A
Using the first law we have:
T
U=Q+W
If we carry out a reversible process, we have
for any point along the path
dU = TdS + dW
If we have work by a expansion of a fluid
dU = TdS − pdV
Monday, January 5, 15
22
Let us look at the very initial stage
H
L
dq is so small that the temperatures of
the two systems do not change
dq
dSH =
TH
For system L
dq
dSL =
TL
Hence, for the total system
⇥
1
1
dS = dSL + dSH = dq
⇥
TL TH
For system H
Heat goes from warm to cold: or if dq > 0 then TH > TL
This gives for the entropy change:
dS > 0
Hence, the entropy increases until the two
temperatures are equal
Monday, January 5, 15
23
Question
•
•
Monday, January 5, 15
Thermodynamics has a sense of
time, but not Newton’s dynamics
•
Look at a water atoms in reverse
•
Look at a movie in reverse
When do molecules know about the
arrow of time?
24
Thermodynamics
(statistical)
Monday, January 5, 15
25
l
Statistical Thermodynamics
a
c cs
i
s
i
s
s
m
Basic assumption la
a
w
c
n
a
For an isolated
system
any
microscopic
l
t
y
u
configuration
is equally
likely n
d
b
o
o
.
Consequence
.. rm ed
e
s
All of statistical
thermodynamics
and
h
a
t thermodynamics
equilibrium
b
is
Monday, January 5, 15
26
Ideal gas
Let us again make an ideal gas
We select:
(1) N particles,
(2) Volume V,
(3) initial velocities
+ positions
This fixes; V/n, U/n
Basic assumption
For an isolated system any microscopic
configuration is equally likely
Monday, January 5, 15
27
What is the probability to find this configuration?
The system has the same kinetic energy!!
Our basic assumption must be seriously wrong!
... but are we doing the statistics correctly?
Monday, January 5, 15
28
Question
•
Monday, January 5, 15
Is it safe to be in this room?
29
... lets look at our statistics correctly
What is the probability to
find this configuration?
Basic
assumption:
1
P=
total # of configurations
number 1 can be put in M positions, number 2 at M
positions, etc
Total number of configurations: M
N
with
V
M=
dr
the larger the volume of the gas the more
configurations
Monday, January 5, 15
30
1
2
7
9
3
4
8
6
5
What is the probability to find the 9
molecules exactly at these 9 positions?
Monday, January 5, 15
✓
V
V
◆N
31
1
3
9
7
8
2
4
5
6
What is the probability to find the 9
molecules exactly at these 9 positions?
Monday, January 5, 15
✓
V
V
◆N
32
4
1
5
9
7
8
6
2
3
What is the probability to find the 9
molecules exactly at these 9 positions?
Monday, January 5, 15
✓
V
V
◆N
33
1
5
4
7
9
2
8
6
3
What is the probability to find the 9
molecules exactly at these 9 positions?
Monday, January 5, 15
✓
V
V
◆N
34
What is the probability to
find this configuration?
exactly equal as to any
other configuration!!!!!!
This is reflecting the microscopic reversibility of
Newton’s equations of motion. A microscopic
system has no “sense” of the direction of time
Are we asking the right question?
Monday, January 5, 15
35
Are we asking the right question?
These are microscopic properties; no irreversibility
Thermodynamic is about macroscopic properties:
Measure densities: what is the
probability that we have all our
N gas particle in the upper half?
N
P(empty)
1
0.5
2
0.5 x 0.5
3
0.5 x 0.5 x 0.5
1000
Monday, January 5, 15
10
-301
36
Summary
•
On a microscopic level all configurations are
equally likely
•
On a macroscopic level; as the number of
particles is extremely large, the probability that
we have a fluctuation from the average value is
extremely low
•
Let us quantify these statements
Monday, January 5, 15
37
Basic assumption
E1 > E2
NVE1
NVE2
Let us look at one of our
examples; let us assume
that the total system is
isolate but heat can flow
between 1 and 2.
All micro states will be equally likely!
... but the number of micro states that give an
particular energy distribution (E1,E-E1) not ...
... so, we observe the most likely one ...
Monday, January 5, 15
38
In a macroscopic system we will observe the most likely one
P(E1 , E2 ) =
N1 (E1 )
E1 =E
E1 =0
N2 (E ⇤ E1 )
N1 (E1 )
N2 (E ⇤ E1 )
The summation only depends on the total energy:
P(E1 , E2 ) = C
N1 (E1 )
N2 (E ⇤ E1 )
ln P(E1 , E2 ) = ln C + ln N1 (E1 ) + ln N2 (E ⌅ E1 )
We need to find the maximum
d ln P(E1 , E2 )
d ln N (E1 , E2 )
=
=0
dE1
dE1
d [ln N1 (E1 ) + ln N2 (E ⌅ E1 )]
=0
dE1
Monday, January 5, 15
39
We need to find the maximum
d [ln N1 (E1 ) + ln N2 (E ⌅ E1 )]
=0
dE1
d ln N1 (E1 )
d ln N2 (E ⇤ E1 )
=⇤
dE1
dE1
As the total energy is constant
E2 = E
E1
dE1 = ⇤d(E ⇤ E1 ) = ⇤dE2
Which gives as equilibrium condition:
d ln N1 (E1 )
d ln N2 (E2 )
=
dE1
dE2
Monday, January 5, 15
40
Let us define a property
(almost S, but not quite) :
Equilibrium if:
or
S * = ln N ( E )
d ln N 1 ( E1 ) d ln N 2 ( E2 )
=
dE1
dE2
⎛ ∂S1* ⎞⎟
⎛ ∂S2* ⎞⎟
⎜⎜
⎟⎟
⎟⎟
= ⎜⎜
⎜⎝ ∂E ⎟⎠
⎜⎝ ∂E ⎟⎠
1 N1 ,V1
And for the total system:
2 N 2 ,V2
S * = S1* + S2*
For a system at constant energy, volume and number of
particles the S* increases until it has reached its maximum
value at equilibrium
What is this magic property S*?
Monday, January 5, 15
41
Defined a property S* (that is almost S):
S * (E1 , E − E1 ) = lnℵ(E1 , E − E1 )
= lnℵ1 (E1 ) + lnℵ2 (E − E1 )
= S1* (E1 ) + S2* (E − E1 )
Why is maximizing S* the same as maximizing N?
The logarithm is a monotonically increasing function.
Why else is the logarithm a convenient function?
Makes S* additive! Leads to extensivity.
Why is S* not quite entropy?
Units! The logarithm is just a unitless quantity.
Monday, January 5, 15
42
Thermal Equilibrium (Review)
E1 > E2
NVE1
NVE2
Isolated system that
allows heat flow
between 1 and 2.
ℵ(E1 , E − E1 ) = ℵ1 (E1 )iℵ2 (E − E1 )
Number of micro states that give an particular
energy distribution (E1,E-E1) is maximized with
respect to E1.
Monday, January 5, 15
43
For a partitioning of E between 1 and 2, the number
of accessible states is maximized when:
⎛ ∂S1* ⎞⎟
⎜⎜
⎟⎟
⎜⎝ ∂E ⎟⎠
1 N1 ,V1
⎛ ∂S2* ⎞⎟
⎟⎟
= ⎜⎜
⎜⎝ ∂E ⎟⎠
2 N 2 ,V2
What do these partial derivatives relate to?
Thermal equilibrium --> Temperature!
M
dE = TdS-pdV + ∑ µi dN i
i =1
Temperature
Monday, January 5, 15
⎛ ∂E ⎞
T =⎜ ⎟
⎝ ∂S ⎠ V , Ni
or
1 ⎛ ∂S ⎞
=⎜ ⎟
T ⎝ ∂E ⎠ V , Ni
44
Summary
•
Statistical Mechanics:
•
basic assumption:
•
•
Monday, January 5, 15
all microstates are equally likely
Applied to NVE
•
Definition of Entropy: S = kB ln Ω
•
Equilibrium: equal temperatures
45
Question
How large is Ω for a glass of water?
•
For macroscopic systems, super-astronomically
large.
•
For instance, for a glass of water at room
temperature
•
Macroscopic deviations from the second law of
thermodynamics are not forbidden, but they are
extremely unlikely.
Monday, January 5, 15
46
Systems at Constant Temperature
(different ensembles)
Monday, January 5, 15
47
The
nd
2
law
Entropy of an isolated system can only
increase; until equilibrium were it takes its
maximum value
Most systems are at constant temperature
and volume or pressure?
What is the formulation for these systems?
Monday, January 5, 15
48
fixed volume but can
exchange energy
1
Constant T and V
We have our box 1 and a bath
Total system is isolated and
the volume is constant
First law
dU = dq
Second law dS
pdV = 0
0
Box 1: constant volume and temperature
1st law:
dU1 + dUb = 0
or
dU1 =
dUb
The bath is so large that the heat flow does not influence the
temperature of the bath + the process is reversible
2nd
Monday, January 5, 15
dUb
law: dS1 + dSb = dS1 +
T
T dS1 dU1 0
0
49
fixed volume but can
exchange energy
1
Constant T and V
Total system is isolated and
the volume is constant
Box 1: constant volume
and temperature
T dS1
2nd law:
dU1
0
d(U1 ⇤ TS1 )
0
Let us define the Helmholtz free energy: A
For box 1 we can write dA1
A
U
TS
0
Hence, for a system at constant temperature
and volume the Helmholtz free energy decreases
and takes its minimum value at equilibrium
Monday, January 5, 15
50
Canonical ensemble
1/kBT
Consider a small system that can exchange
heat with a big reservoir
Hence, the probability to find Ei:
51
Monday, January 5, 15
Boltzmann distribution
51
Thermodynamics
What is the average energy of the system?
Compare:
52
Monday, January 5, 15
52
Thermodynamics
First law of thermodynamics
Helmholtz Free energy:
53
Monday, January 5, 15
53
What is the average energy of the system?
Compare:
Hence:
54
Monday, January 5, 15
54
Atoms?
We have assumed that we can count states
Quantum Mechanics: energy discreet
What to do for classical model such as an
ideal gas, hard spheres, Lennard-Jones?
Energy is continue:
• potential energy
• kinetic energy
Particle in a box:
εn
2
nh )
(
=
8mL2
What are the energy levels for Argon in
a 1-dimensional box of 1 cm?
Monday, January 5, 15
55
What are the energy levels for Argon in
a 1-dimensional box of 1 cm?
Argon: m=40 g/mol=6.63×10-26 kg
h=6.63×10-34 J s
εn
2
nh )
(
=
8mL2
ε n = 5 × 10 −39 n 2 ( J )
Kinetic energy of Ar at room temperature ≈4.14 × 10-21 J
Many levels are occupied: only
at very low temperatures or
very small volumes one can see qtranslational =
quantum effect!
2
∞
qtranslational = ∫ e
0
3D:
qtranslational
Monday, January 5, 15
−
( nh )
8 mL2 kBT
dn
3
2
qtranslational
V
⎛ 2π mk BT ⎞
=⎜
V= 3
⎟
2
⎝ h
⎠
Λ
∞
∑e
−
( nh )2
8 mL2 kBT
n=1
1
2
⎛ 2π mk BT ⎞
=⎜
L
⎟
2
⎝ h
⎠
De Broglie
wavelength
56
∞
q = ∑ e− En = ∫ e− En dn
Partition function;
n=1
Hamiltonian:
H = U kin + U pot
Z1,V ,T = C ∫ e
pi2
= ∑i
+ U pot ( r N )
2mi
p2
−
2 m kBT
dp 3N ∫ e
−
U p (r )
kBT
dr 3N
One ideal gas molecule: Up(r)=0
IG
1,V ,T
Z
qtranslational
= C∫e
dp ∫ dr = CV ( 2π mkBT )
3
2
3
2
V
⎛ 2π mkBT ⎞
=⎜
V= 3
⎝ h 2 ⎟⎠
Λ
IG
1,V ,T
Z
Monday, January 5, 15
p2
−
2 m kBT
= CV ( 2π mkBT )
3
2
V
= 3
Λ
57
N gas molecules:
Z N ,V ,T
Z N ,V ,T
1
= 3N ∫ e
h
p2
−
2 m kBT
1
= 3N ∫ e
h N!
dp N ∫ e
p2
−
2 m kBT
−
U(r )
kBT
dp N ∫ e
−
dr N
U(r )
kBT
WRONG!
Particles are
indistinguishable
dr N
Configurational part of
the partition function:
QN ,V ,T =
Monday, January 5, 15
1
Λ 3N N!
∫e
−
U(r )
kBT
dr N
58
Question
•
Monday, January 5, 15
For an ideal gas, calculate:
•
the partition function
•
the pressure
•
the energy
•
the chemical potential
59
ideal gas molecules:
QNIG,V ,T
VN
= 3N
Λ N!
All thermodynamics follows from the partition function!
Free energy:
F IG = −kBT lnQNIG,V ,T = kBTN ⎡⎣ ln Λ 3 − ln (V N ) ⎤⎦
F IG = F 0 + k BTN ln ρ
Pressure:
Energy:
1
⎛ ∂F ⎞
p = −⎜
= k BTN
⎟
⎝ ∂V ⎠ T ,N
V
⎛ ∂F T ⎞
⎛ ∂ln Λ ⎞
E=⎜
= 3kB N ⎜
⎟
⎝ ∂1 T ⎠ V ,N
⎝ ∂1 T ⎟⎠ V ,N
3
E = Nk BT
2
Monday, January 5, 15
⎛ h2 ⎞
Λ=⎜
⎝ 2π mkBT ⎟⎠
1
2
60
⎛ ∂F ⎞
µi = ⎜
⎝ ∂N i ⎟⎠ T ,V , N j
Chemical potential:
⎛ N⎞
β F = N ln Λ + N ln ⎜ ⎟
⎝V ⎠
3
βµ = ln Λ 3 + ln ρ + 1
βµ IG = βµ 0 + ln ρ
61
Monday, January 5, 15
61
Summary:
Canonical ensemble (N,V,T)
Partition function:
Probability to find a particular configuration
Free energy
62
Monday, January 5, 15
62
Summary:
micro-canonical ensemble (N,V,E)
Partition function:
Probability to find a particular configuration
Free energy
63
Monday, January 5, 15
63
Other Ensemble
Monday, January 5, 15
64
Other ensembles?
COURSE:
In the thermodynamic limit the thermodynamic properties are
MD and MC different
independent of the ensemble: so buy a bigger computer
…
ensembles
However, it is most of the times much better to think and to
carefully select an appropriate ensemble.
For this it is important to know how to simulate in the various
ensembles.
But for doing this wee need to know the Statistical
Thermodynamics of the various ensembles.
65
Monday, January 5, 15
65
Example (1):
vapour-liquid equilibrium mixture
T
V
L
L+V
Measure the composition of
the coexisting vapour and
liquid phases if we start
with a homogeneous liquid
of two different
compositions:
•
How to mimic this with
the N,V,T ensemble?
•
What is a better
ensemble?
composition
66
Monday, January 5, 15
66
Example (2): swelling of clays
Deep in the earth clay layers
can swell upon adsorption
of water:
•
How to mimic this in the
N,V,T ensemble?
•
What is a better ensemble
to use?
67
Monday, January 5, 15
67
Ensembles
•
Micro-canonical ensemble: E,V,N
•
Canonical ensemble: T,V,N
•
Constant pressure ensemble: T,P,N
•
Grand-canonical ensemble: T,V,µ
68
Monday, January 5, 15
68
Constant pressure
Monday, January 5, 15
69
fixed N but can exchange
energy + volume
1
We have our box 1 and a bath
Total system is isolated and
the volume is constant
First law
dU = dq
pdV = 0
Second law dS
0
Box 1: constant pressure and temperature
dU1 = dUb
or
1st law: dU1 + dUb = 0
dV1 + dVb = 0
dV1 = dVb
or
The bath is very large and the small changes do not
change P or T; in addition the process is reversible
2nd
dUb
p
+ dVb
law: dS1 + dSb = dS1 +
T
T
T dS1 dU1 pdV1
Monday, January 5, 15
0
0
70
fixed N but can exchange
energy + volume
1
Total system is isolated and
the volume is constant
Box 1: constant pressure
and temperature
2nd law: T dS1
Let us define the
Gibbs free energy: G
For box 1 we can write
G
dG1
dU1 pdV1
d(U1 ⌅ TS1 + pV1 )
U ⇥ TS + pV
0
0
0
Hence, for a system at constant temperature and
pressure the Gibbs free energy decreases and
takes its minimum value at equilibrium
Monday, January 5, 15
71
N,P,T ensemble
Consider a small system that
can exchange volume and
energy with a big reservoir
The terms in the expansion follow from
the connection with Thermodynamics:
We have:
1
p
µi
dS = dU + dV − ∑ dN i
T
T
T
1
⎛ ∂S ⎞
=
⎜⎝
⎟⎠
∂U V ,Ni T
Monday, January 5, 15
S = kB ln Ω
and
p
⎛ ∂S ⎞
=
⎜⎝
⎟⎠
∂V E,Ni T
72
⎛ ∂ ln Ω ⎞
⎛ ∂ ln Ω ⎞
ln Ω (V − Vi , E − Ei ) = ln Ω (V, E ) − ⎜
Ei − ⎜
Vi +!
⎟
⎟
⎝ ∂E ⎠ V ,N
⎝ ∂V ⎠ E,N
Ei
p
ln Ω (V − Vi , E − Ei ) = ln Ω (V, E ) −
−
Vi
k BT k BT
Hence, the probability to find Ei,Vi:
Monday, January 5, 15
73
Partition function:
Ensemble average:
pVj ⎤
⎡ Ei
Δ ( N, P,T ) = ∑ i, j exp ⎢ −
−
⎥
k
T
k
T
⎣ B
B ⎦
pVj ⎤
⎡ Ei
∑ i, j Vj exp ⎢ − k T − k T ⎥
⎛ ∂ ln Δ ⎞
⎣
B
B ⎦
V =
= −kBT ⎜
⎝ ∂p ⎟⎠ T ,N
Δ ( N, p,T )
Thermodynamics
Hence:
Monday, January 5, 15
dG = −SdT + Vdp + ∑ µi dN i
⎛ ∂G ⎞
V =⎜
⎝ ∂p ⎟⎠ T ,N
G
= − ln Δ ( N, p,T )
k BT
74
Summary
In the classical limit, the partition
function becomes
The probability to find a particular
configuration:
75
Monday, January 5, 15
75
grand-canonical ensemble
Monday, January 5, 15
76
Grand-canonical ensemble
Classical
•
A small system that can exchange heat and
particles with a large bath
Statistical
•
Taylor expansion of a small reservoir
Monday, January 5, 15
77
exchange energy and
particles
1
Constant T and μ
Total system is isolated
and the volume is constant
First law
dU = TdS − pdV + µdN = 0
Second law dS 0
Box 1: constant chemical potential and temperature
or dU1 = dUb
1st law: dU1 + dUb = 0
or
dN1 + dN b = 0
dN b = −dN1
The bath is very large and the small changes do not
change μ or T; in addition the process is reversible
2nd law:
Monday, January 5, 15
1
µb
dS1 + dSb = dS1 + dU b − dN b ≥ 0
Tb
Tb
78
1
µb
dS1 + dSb = dS1 + dU b − dN b ≥ 0
Tb
Tb
We can express the changes of the bath in terms of
properties of the system
1
µ
dS1 − dU1 + dN1 ≥ 0
d (TS1 − U1 + µ N1 ) ≥ 0
T
T
d (U − TS − µ N ) ≤ 0
For the Gibbs free energy we can write:
G ≡ U − TS + pV
G = µN
or
d ( − pV ) ≤ 0
or
Giving:
− pV = U − TS − µ N
d ( pV ) ≥ 0
Hence, for a system at constant temperature
and chemical potential pV increases and
takes its maximum value at equilibrium
Monday, January 5, 15
79
µ,V,T ensemble
Consider a small system that can
exchange particles and energy
with a big reservoir
⎛ ∂ ln Ω ⎞
⎛ ∂ ln Ω ⎞
ln Ω E − Ei , N − N j , = ln Ω ( E, N ) − ⎜
Ei − ⎜
N j +!
⎟
⎟
⎝ ∂E ⎠ V ,N
⎝ ∂N ⎠ E,V
(
)
The terms in the expansion follow from
the connection with Thermodynamics:
1
p
µ
dS = dU + dV − dN
T
T
T
S = kB ln Ω
µ
⎛ ∂S ⎞
⎜⎝
⎟⎠ = −
∂N E,V
T
1
⎛ ∂S ⎞
⎜⎝
⎟⎠ =
∂U V ,N T
80
Monday, January 5, 15
80
⎛ ∂ ln Ω ⎞
⎛ ∂ ln Ω ⎞
ln Ω E − Ei , N − N j , = ln Ω ( E, N ) − ⎜
Ei − ⎜
N j +!
⎟
⎟
⎝ ∂E ⎠ V ,N
⎝ ∂N ⎠ E,V
(
)
Ei
µ
ln Ω E − Ei , N − N j = ln Ω ( E, N ) −
+
Nj
k BT k BT
(
ln
)
(
Ω E − Ei , N − N j
Ω ( E, N )
)=−
Ei
µ
+
Nj
k BT k BT
Hence, the probability to find Ei,Nj:
(
Ω E − Ei , N − N j
)
⎡ Ei
µ Ni ⎤
P Ei , N j =
∝ exp ⎢ −
+
⎥
k
T
k
T
Ω
E
−
E
,
N
−
N
∑ k,l (
⎣ B
⎦
B
k
l)
(
Monday, January 5, 15
)
81
μ,V,T ensemble (2)
In the classical limit, the partition
function becomes
The probability to find a particular
configuration:
82
Monday, January 5, 15
82