Download Chapter 14

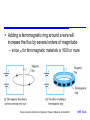
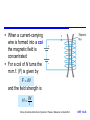
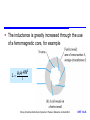
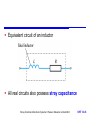
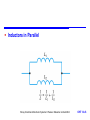
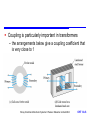
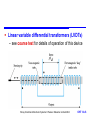
Inductance and Magnetic Fields














Chapter 14
Introduction
Electromagnetism
Reluctance
Inductance
Self-inductance
Inductors
Inductors in Series and Parallel
Voltage and Current
Sinusoidal Voltages and Currents
Energy Storage in an Inductor
Mutual Inductance
Transformers
Circuit Symbols
The Use of Inductance in Sensors
Storey: Electrical & Electronic Systems © Pearson Education Limited 2004
OHT 14.‹#›
Introduction
14.1
 Earlier we noted that capacitors store energy by
producing an electric field within a piece of dielectric
material
 Inductors also store energy, in this case it is stored
within a magnetic field
 In order to understand inductors, and related
components such as transformers, we need first to
look at electromagnetism
Storey: Electrical & Electronic Systems © Pearson Education Limited 2004
OHT 14.‹#›
Electromagnetism
14.2
 A wire carrying a
current I causes a
magnetomotive
force (m.m.f) F
– this produces a
magnetic field
– F has units of
Amperes
– for a single wire
F is equal to I
Storey: Electrical & Electronic Systems © Pearson Education Limited 2004
OHT 14.‹#›
 The magnitude of the field is defined by the
magnetic field strength, H , where
HI
l
where l is the length of the magnetic circuit
 Example – see Example 14.1 from course text
A straight wire carries a current of 5 A. What is the magnetic
field strength H at a distance of 100mm from the wire?
Magnetic circuit is circular. r = 100mm, so path = 2r = 0.628m
I
5
H 
 7.96 A /m
l 0.628
Storey: Electrical & Electronic Systems © Pearson Education Limited 2004
OHT 14.‹#›
 The magnetic field produces a magnetic flux, 
– flux has units of weber (Wb)
 Strength of the flux at a particular location is measured
in term of the magnetic flux density, B
– flux density has units of tesla (T) (equivalent to 1 Wb/m2)
 Flux density at a point is determined by the field
strength and the material present
or
B  μ0 μ r H
B  μH
where  is the permeability of the material, r is the relative
permeability and 0 is the permeability of free space
Storey: Electrical & Electronic Systems © Pearson Education Limited 2004
OHT 14.‹#›
 Adding a ferromagnetic ring around a wire will
increase the flux by several orders of magnitude
– since r for ferromagnetic materials is 1000 or more
Storey: Electrical & Electronic Systems © Pearson Education Limited 2004
OHT 14.‹#›
 When a current-carrying
wire is formed into a coil
the magnetic field is
concentrated
 For a coil of N turns the
m.m.f. (F) is given by
F  IN
and the field strength is
H  IN
l
Storey: Electrical & Electronic Systems © Pearson Education Limited 2004
OHT 14.‹#›
 The magnetic flux produced is determined by the
permeability of the material present
– a ferromagnetic material will increase the flux density
Storey: Electrical & Electronic Systems © Pearson Education Limited 2004
OHT 14.‹#›
Reluctance
14.3
 In a resistive circuit, the resistance is a measure of
how the circuit opposes the flow of electricity
 In a magnetic circuit, the reluctance, S is a measure
of how the circuit opposes the flow of magnetic flux
 In a resistive circuit R = V/I
 In a magnetic circuit
SF
Φ
– the units of reluctance are amperes per weber (A/ Wb)
Storey: Electrical & Electronic Systems © Pearson Education Limited 2004
OHT 14.‹#›
Inductance
14.4
 A changing magnetic flux induces an e.m.f. in any
conductor within it
 Faraday’s law:
The magnitude of the e.m.f. induced in a circuit is
proportional to the rate of change of magnetic flux
linking the circuit
 Lenz’s law:
The direction of the e.m.f. is such that it tends to
produce a current that opposes the change of flux
responsible for inducing the e.m.f.
Storey: Electrical & Electronic Systems © Pearson Education Limited 2004
OHT 14.‹#›
 When a circuit forms a single loop, the e.m.f. induced
is given by the rate of change of the flux
 When a circuit contains many loops the resulting e.m.f.
is the sum of those produced by each loop
 Therefore, if a coil contains N loops, the induced
voltage V is given by
V  N dΦ
dt
where d/dt is the rate of change of flux in Wb/s
 This property, whereby an e.m.f. is induced as a result
of changes in magnetic flux, is known as inductance
Storey: Electrical & Electronic Systems © Pearson Education Limited 2004
OHT 14.‹#›
Self-inductance
14.5
 A changing current in a wire causes a changing
magnetic field about it
 A changing magnetic field induces an e.m.f. in
conductors within that field
 Therefore when the current in a coil changes, it
induces an e.m.f. in the coil
 This process is known as self-inductance
V  L dI
dt
where L is the inductance of the coil (unit is the Henry)
Storey: Electrical & Electronic Systems © Pearson Education Limited 2004
OHT 14.‹#›
Inductors
14.6
 The inductance of a coil depends on its dimensions
and the materials around which it is formed
μ0 AN 2
L
l
Storey: Electrical & Electronic Systems © Pearson Education Limited 2004
OHT 14.‹#›
 The inductance is greatly increased through the use
of a ferromagnetic core, for example
μ0 μr AN 2
L
l
Storey: Electrical & Electronic Systems © Pearson Education Limited 2004
OHT 14.‹#›
 Equivalent circuit of an inductor
 All real circuits also possess stray capacitance
Storey: Electrical & Electronic Systems © Pearson Education Limited 2004
OHT 14.‹#›
Inductors in Series and Parallel
14.7
 When several inductors are connected together their
effective inductance can be calculated in the same
way as for resistors – provided that they are not
linked magnetically
 Inductors in Series
Storey: Electrical & Electronic Systems © Pearson Education Limited 2004
OHT 14.‹#›
 Inductors in Parallel
Storey: Electrical & Electronic Systems © Pearson Education Limited 2004
OHT 14.‹#›
Voltage and Current
14.8
 Consider the circuit shown here
– inductor is initially un-energised
 current through it will be zero
– switch is closed at t = 0
– I is initially zero
 hence VR is initially 0
 hence VL is initially V
– as the inductor is energised:




I increases
VR increases
hence VL decreases
we have exponential behaviour
Storey: Electrical & Electronic Systems © Pearson Education Limited 2004
OHT 14.‹#›
 Time constant
– we noted earlier that in a capacitor-resistor circuit the
time required to charge to a particular voltage is
determined by the time constant CR
– in this inductor-resistor circuit the time taken for the
current to rise to a certain value is determined by L/R
– this value is again the time constant  (greek tau)
 See Computer Simulation Exercises 14.1 and 14.2
in the course text
Storey: Electrical & Electronic Systems © Pearson Education Limited 2004
OHT 14.‹#›
Sinusoidal Voltages and Currents
14.9
 Consider the application of a
sinusoidal current to an inductor
– from above V = L dI/dt
– voltage is directly proportional to
the differential of the current
– the differential of a sine wave is
a cosine wave
– the voltage is phase-shifted by
90 with respect to the current
– the phase-shift is in the opposite
direction to that in a capacitor
Storey: Electrical & Electronic Systems © Pearson Education Limited 2004
OHT 14.‹#›
Energy Storage in an Inductor
14.10
 Can be calculated in a similar manner to the energy
stored in a capacitor
 In a small amount of time dt the energy added to the
magnetic field is the product of the instantaneous
voltage, the instantaneous current and the time
di
Energy added  vi dt  L idt  Li di
dt
 Thus, when the current is increased from zero to I
1 2
E  L  idt  LI
0
2
I
Storey: Electrical & Electronic Systems © Pearson Education Limited 2004
OHT 14.‹#›
Mutual Inductance
14.11
 When two coils are linked magnetically then a
changing current in one will produce a changing
magnetic field which will induce a voltage in the other
– this is mutual inductance
 When a current I1 in one circuit, induces a voltage V2
in another circuit, then
dI
V M 1
dt
2
where M is the mutual inductance between the circuits. The
unit of mutual inductance is the Henry (as for self-inductance)
Storey: Electrical & Electronic Systems © Pearson Education Limited 2004
OHT 14.‹#›
 The coupling between the coils can be increased by
wrapping the two coils around a core
– the fraction of the magnetic field that is coupled is
referred to as the coupling coefficient
Storey: Electrical & Electronic Systems © Pearson Education Limited 2004
OHT 14.‹#›
 Coupling is particularly important in transformers
– the arrangements below give a coupling coefficient that
is very close to 1
Storey: Electrical & Electronic Systems © Pearson Education Limited 2004
OHT 14.‹#›
Transformers
14.12
 Most transformers approximate to ideal components
– that is, they have a coupling coefficient  1
– for such a device, when unloaded, their behaviour is
determined by the turns ratio
– for alternating voltages
V
N
2 2
V
N
1
1
Storey: Electrical & Electronic Systems © Pearson Education Limited 2004
OHT 14.‹#›
 When used with a resistive load, current flows in the
secondary
– this current itself produces a magnetic flux which
opposes that produced by the primary
– thus, current in the
secondary reduces
the output voltage
– for an ideal transformer
V1 I1  V2 I2
Storey: Electrical & Electronic Systems © Pearson Education Limited 2004
OHT 14.‹#›
Circuit Symbols
Storey: Electrical & Electronic Systems © Pearson Education Limited 2004
14.13
OHT 14.‹#›
The Use of Inductance in Sensors
14.14
 Numerous examples:
 Inductive proximity
sensors
– basically a coil
wrapped around a
ferromagnetic rod
– a ferromagnetic plate coming close to the coil changes
its inductance allowing it to be sensed
– can be used as a linear sensor or as a binary switch
Storey: Electrical & Electronic Systems © Pearson Education Limited 2004
OHT 14.‹#›
 Linear variable differential transformers (LVDTs)
– see course text for details of operation of this device
Storey: Electrical & Electronic Systems © Pearson Education Limited 2004
OHT 14.‹#›
Key Points
 Inductors store energy within a magnetic field
 A wire carrying a current creates a magnetic field
 A changing magnetic field induces an electrical voltage in
any conductor within the field
 The induced voltage is proportional to the rate of change of
the current
 Inductors can be made by coiling wire in air, but greater
inductance is produced if ferromagnetic materials are used
 The energy stored in an inductor is equal to ½LI2
 When a transformer is used with alternating signals, the
voltage gain is equal to the turns ratio
Storey: Electrical & Electronic Systems © Pearson Education Limited 2004
OHT 14.‹#›