Download Data Display

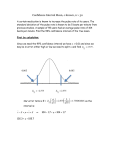
CHAPTER 12
Section 12.4 General Confidence Interval for One Mean or Paired Data
1.
Determining the t-multiplier for a confidence interval.
In Section 12.4 of the book, you find the description of the multiplier t* as
“For a confidence interval for a population mean, the multiplier t* is the value in a tdistribution with df = n-1 such that the area between –t* and +t* equals the desired
confidence level.”
So given a confidence level, for example 95%, we need to find the value t* such that
P(-t*  t  t*)=0.95, where t is a random variable with the Student’s t-distribution with
n-1 degrees of freedom (n being the number of observations or the number of pairs in a
x
matched pairs design). In this specific case t 
s
n
In the graph below, the t-distribution with 8 degrees of freedom is displayed. The values
t* and –t* we are looking for are marked by the red lines. The area in the center is 0.95
and since the total area under the curve is 1, the area of each tail is 0.025. Therefore the
area accumulated up to the value t* is 0.025+0.95=0.975
0.4
f(t)
0.3
0.2
0.95
0.1
0.025
0.025
0.0
-4
-3
-2
-1
0
1
2
3
4
t
From the main menu, select Calc > Probability Distributions > t
Select the Inverse cumulative probability option, because we are trying to find the value
t* such that the cumulative probability up to that point is 0.975. Type the number 8 in the
Degrees of freedom dialog box and type 0.975 in the Input constant dialog box.
117
The output is:
Inverse Cumulative Distribution Function
Student's t distribution with 8 DF
P( X <= x )
0.975
x
2.30600
The value 2.0306 has been rounded to 2.31 in example 12.5 in the book.
If the desired confidence is 90%, then the value to type in the Input constant dialog box
would be 0.95; if the desired confidence is 99%, then the value to input will be 0.995. In
general, the value to input in the Input constant dialog box is the value of the central area
under the curve plus the area of the left tail. The t-distribution is symmetric, so once we
have found t*, we automatically have -t*.
(Alternatively) Use Graph > Probability Distribution Plot > View Probability
Select t Distribution with 8 degrees of freedom as shown below.
118
Select Shaded Area, Probability, Middle and enter 0.025 in the two dialog boxes.
Clicking OK gives the multiplier t* = 2.31.
119
Distribution Plot
T, df=8
0.4
0.95
Density
0.3
0.2
0.1
0.0
2.
-2.31
0
X
2.31
Constructing a confidence interval for a single mean
Example 12.5 describes the estimation of the mean length of a males forearm based on a
sample of 9 values. The observations are:
25.5
24.0
26.5
25.5
28.0
27.0
23.0
25.0
25.0
In order to construct the confidence interval we need the mean and the standard deviation
s
of the sample in order to work with the formula: x  t *
.
n
Select Stat > Basic Statistics > Store Descriptive Statistics to open the window and
click on the Statistics button, to see all the options. From the available statistics pick
Mean and Standard deviation.
120
Click OK on both windows and the value of those statistics will appear in the first two
columns that are free, in this case
Mean
25.5
StDev1
1.52069
In the previous section, we found that for 95% confidence the value of t* is 2.3060 when
df = 8. Therefore the bounds (endpoints) of the confidence interval are:
25 .5  2.4060
1.52069
9
and 25 .5  2.4060
1.52069
9
121
These calculations can be performed by typing the commands at the MTB> prompt. Type
the expressions of the formula and assign the values to the constants K1 and K2:
MTB> let k1=25.5-2.3060*1.52069/sqrt(9)
MTB > let k2=25.5+2.3060*1.52069/sqrt(9)
MTB > print k1 k2
The output is
Data Display
K1
K2
24.3311
26.6689
We are 95% confident that the mean length of the forearm for the population of men from
where the random sample was taken is between 24.33 and 26.67.
You can also obtain the confidence interval by letting Minitab perform all the
calculations. Type the data in column C1 and then click on Stat > Basic Statistics > 1Sample t. Once the window 1-Sample t (Test and Confidence Interval) appears, select
C1 for the Samples in columns: dialog box. Click on the Options button, and indicate the
level of confidence you want (95%). To get a two-sided confidence interval, like the one
in the book, select the option not equal in the Alternative dialog box. Click OK to return
to the 1-Sample t window and then click OK again.
122
The output is:
One-Sample T: length
Variable
length
N
9
Mean
25.5000
StDev
1.5207
SE Mean
0.5069
95% CI
(24.3311, 26.6689)
This is the same interval shown in the book with the numbers rounded to two decimal
places.
3.
Checking the conditions before finding a confidence interval for the mean.
The t-confidence interval is valid either if the variable has a normal distribution
(regardless of sample size) or if the random sample is large. Situations when the data has
extreme outliers or strong skewness require larger samples for the t-confidence interval to
be reliable. T-confidence intervals should not be used in small samples with severe
skewness or outliers.
Example 12.6 works with two groups of data; the second group (Stat 13) has 148
students. The sample is large so the t-confidence interval would work even if the
distribution of the hours of sleep were not normal. The first sample (n=25) is not large
and it is necessary to check its distribution before working with the t-confidence interval.
The boxplot is a useful graph to check for severe skewness and the presence of outliers.
Open the data file UCDavis1.mtw, the name of the class might appear as NonLib and
LibArts instead of Stat 10 and Stat 13. We used Data > Code > Text to Text to change
NonLib into Stat13 and LibArts into Stat10.
Use Graph > Boxplot > With Groups to obtain the boxplot window and enter sleep as
Graph variables: and class as Categorical variables for grouping (1-4, outermost first):
The small sample does not present any outlier. Fortunately the number of observations in
Stat 13 is ‘large enough’ (n=148) for its lack of normality to be of no serious
consequence.
123
Boxplot of Sleep
12
10
Sleep
8
6
4
2
Stat10
Stat13
class
We will now be working with the smaller group, so use Data > Unstack to separate the
content of the column Sleep into two columns, one for each class. Two new columns will
appear at the end of the worksheet: Sleep_Stat 10 and Sleep_Stat 13. Fill-in the dialog
boxes and select After last column in use as shown below.
124
Clicking OK will produce a histogram with 11 intervals. Since there are only 25
observations for Class 10 (Sleep_Stat10) we do not want to have a histogram with too
many intervals; rather, we would like to have a small number of intervals, like 5. Doubleclick on the x-axis of your histogram and select Binning to control for the number of
intervals.
125
Histogram of Sleep_Stat10
9
8
7
Frequency
6
5
4
3
2
1
0
6
7
8
Sleep_Stat10
9
10
The histogram does not indicate any serious departure from normality that would
compromise the validity of the t-confidence interval. Alternatively to the histogram, the
dotplot (see Graph menu) or the stem-and-leaf display (also in the Graph menu) could
be used.
126
Stem-and-Leaf Display: Sleep_Stat10
Stem-and-leaf of Sleep_Stat10
Leaf Unit = 0.10
1
5
6
11
12
(7)
6
5
5
6
6
7
7
8
8
9
N
= 25
5
0000
5
00000
5
0000000
5
00
HI 100, 100, 105
Dotplot of Sleep_Stat10
5.6
4.
6.3
7.0
7.7
8.4
Sleep_Stat10
9.1
9.8
10.5
Computing a confidence interval for a single mean
To obtain the confidence intervals for Example 12.6, select Stat > Basic Statistics > 1Sample t from the menu and fill-in the dialog box with the variables Sleep_Stat10 and
Sleep_Stat13 as shown below.
127
Click on the Options button to open the 1-Sample t Options window; where you need to
indicate the desired confidence. Since we are looking for confidence intervals with a
lower and an upper bound, select not equal in the Alternative dialog box.
Click OK to return to the 1-Sample t window and now click on the Graphs button.
Select the graphs you want and click OK.
128
These graphs not only display the data in the sample but also the mean of the sample and
the confidence interval. These graphs can be used to display the confidence interval and
to check for the conditions as well.
Note. To display these graphs on the same page, select Editor > Layout Tool, change
Columns: to 3, and select a graph from the list to the highlighted cell of the layout.
129
Boxplot of Sleep_Stat13
Histogram of Sleep_Stat13
(with 95% t-confidence interval for the mean)
Individual Value Plot of Sleep_Stat13
(with 95% t-confidence interval for the mean)
(with 95% t-confidence interval for the mean)
24
Frequency
18
12
6
_
X
_
X
_
X
0
4
8
12
3.0
4.5
6.0
Sleep_Stat13
7.5
9.0
10.5
12.0
4
Sleep_Stat13
Boxplot of Sleep_Stat10
(with 95% t-confidence interval for the mean)
8
12
Sleep_Stat13
Histogram of Sleep_Stat10
Individual Value Plot of Sleep_Stat10
(with 95% t-confidence interval for the mean)
(with 95% t-confidence interval for the mean)
8
Frequency
6
4
2
_
X
_
X
_
X
0
5.0
7.5
Sleep_Stat10
5.
10.0
6
7
8
9
Sleep_Stat10
10
5.0
7.5
10.0
Sleep_Stat10
Finding pair differences from raw data
See Example 12.7. The data displayed in Table 12.1 can be found in the file
UCDavis1.mtw, but they correspond only to the class called LibArts. So, we need to
split the worksheet in two: one for NonLib and the other for LibArts. From the menu,
select Data>Split Worksheet.
130
Two new worksheets will appear, one for LibArts with 25 observations and the other for
NonLib with 148 observations. The first worksheet (Class=LibArts) contains, in columns
C2 and C3, the data in Table 12.1 for TV and computer.
The differences (computer-TV) will be calculated and stored in C13. Type the name of
C13 as Comp-TV. To calculate the difference computer-TV there are two options: one
way is to type a command at the MTB> prompt
MTB> let c13=c3-c2
Or use Calc>Calculator from the menu and fill-in the dialog boxes as shown below.
The data contained in columns C2, C3, and C13 are the same as Table 12.1.
131
Row
computer
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
6.
30
20
10
10
10
0
35
20
2
5
10
4
50
5
8
30
40
15
40
3
21
2
9
14
21
TV
2.0
1.5
14.0
2.0
6.0
20.0
14.0
1.0
14.0
10.0
15.0
2.0
10.0
6.0
20.0
20.0
35.0
15.0
5.0
13.5
35.0
1.0
4.0
0.0
14.0
Comp-TV
28.0
18.5
-4.0
8.0
4.0
-20.0
21.0
19.0
-12.0
-5.0
-5.0
2.0
40.0
-1.0
-12.0
10.0
5.0
0.0
35.0
-10.5
-14.0
1.0
5.0
14.0
7.0
Checking the conditions before finding a confidence interval for paired data
Use the options stem-and-leaf display, histogram, dotplot or boxplot (from the Graph
menu) to examine if the difference Computer-TV, which is the new variable in Example
12.7, satisfies the necessary condition to use the t-confidence interval. Since the sample
size is only 25, it is necessary to check for outliers or extreme lack of symmetry.
Boxplot of Comp-TV
40
30
Comp-TV
20
10
0
-10
-20
There are no outliers according to the boxplot. The histogram does not show a serious
departure from normality either. Therefore the t-confidence interval can be calculated
using the differences Comp-TV.
132
Histogram of Comp-TV
6
Frequency
5
4
3
2
1
0
7.
-16
-8
0
8
16
Comp-TV
24
32
40
Calculating a confidence interval for paired data
The formula for the confidence interval for paired data is the same as the formula for the
confidence interval for one mean, only now the variable is the difference.
s
s
So x  t *
converts into d  t * d where sd is the standard deviation of the
n
n
differences. The formula can also be written as d  t *s.e.(d ) , see Example 12.7 in the
book.
This confidence interval can be calculated in three ways using Minitab (a, b, or c as
follows). The first way is by doing the calculations using the formula; the other two
methods use menu options that automatically calculate the interval.
a) Calculating the mean and standard deviation of the differences and applying the
formula above:
Using Stat>Basic Statistics> Store Descriptive Statistics one can calculate the mean
and standard deviation of the differences
Mean1
StDev1
Descriptive Statistics: Comp-TV
Variable
Comp-TV
N
25
N*
0
Mean
5.36
StDev
15.24
We also need the value of t* for 90% confidence and 24 degrees of freedom because
there are 25 observations. Use Calc>Probability Distributions> t, as shown below, to
find the t* value. The value t* is found to be 1.7109.
133
To obtain the confidence interval, commands can be typed at the MTB> prompt
MTB > let k1=5.36-1.7109*15.2428/sqrt(25)
MTB > let k2=5.36+1.7109*15.2428/sqrt(25)
MTB > print k1 k2
K1
K2
0.144219
10.5758
These are the same values, rounded to two decimal places, reported in the book in
Example 12.7.
b) Calculating the confidence interval using the 1-sample t option with the
difference data.
Use Stat>Basic Statistics>1-Sample t to obtain the following window and select CompTV for the Samples in columns dialog box. Click on Options to specify the desired
confidence.
134
Enter 90 in the Confidence level dialog box.
The output is:
One-Sample T: Comp-TV
Variable
Comp-TV
c)
N
25
Mean
5.36000
StDev
15.24284
SE Mean
3.04857
90% CI
(0.14426, 10.57574)
The third option is the one that requires the least work. It works with the
original variables computer and TV, and the option Stat>Basic Statistics>
Paired t. Fill in the dialog boxes as shown below and then select Options.
135
Enter 90 in the Confidence level dialog box.
The output is:
Paired T-Test and CI: computer, TV
Paired T for computer - TV
computer
TV
Difference
N
25
25
25
Mean
16.5600
11.2000
5.36000
StDev
13.8446
9.7029
15.24284
SE Mean
2.7689
1.9406
3.04857
90% CI for mean difference: (0.14426, 10.57574)
T-Test of mean difference = 0 (vs not = 0): T-Value = 1.76 P-Value = 0.091
136
Section 12.5 General Confidence Interval for the Difference between two means
(independent samples)
1.
Checking conditions before computing a confidence interval for the
difference between two independent means.
In Section 12.5, Example 12.9 compares men and women in terms of mean sleep time.
The data are in the file UCDavis1.mtw; only the students in the NonLib class will be
considered. Using Data>Split Worksheet we previously separated the file into two
worksheets: one for the students in Liberal Arts and the other for the students in Non
Liberal Arts. The worksheet below contains Non Liberal Arts (NonLib) students.
The conditions necessary for the t-confidence intervals to be valid need to be checked for
both the male and female groups. The distributions of the sleep times for each group need
to be normal, or at least should not have severe skewness and outliers, especially if the
sample size is small. In this case, both samples are large; there are 83 females and 65
males, so departures from normality would not seriously affect the validity of the tconfidence interval.
To check for the shape of the distribution of hours of sleep for women and for men
several options of the Graph menu can be used: histogram, boxplot, stem-and-leaf
display and dotplot. The boxplot and dotplot windows (with groups) appear below with
their respective dialog boxes filled in and the plots are displayed.
137
Boxplot of Sleep vs Sex
12
10
Sleep
8
6
4
2
Female
Male
Sex
138
Sex
Dotplot of Sleep vs Sex
Female
Male
2.8
4.2
5.6
7.0
Sleep
8.4
9.8
11.2
Neither group presents severe skewness (actually, they look pretty symmetric) or outliers
as can be seen from the graphs.
2.
Calculating the confidence interval for the difference between two
independent means - pooled and unpooled versions.
In the pooled version, the population variances of the measurements (sleep times) in the
two populations (men and women) are considered to be equal. Since they are assumed to
be equal it makes sense to have a single estimate for the variance (‘pooled’ version). The
sample variances of the measurements for both groups are combined to provide a better
estimate of the common variance. Under the assumption of equal variance, the number of
degrees of freedom is n1 + n2 - 2.
139
From the menu, select Stat>Basic Statistics> 2-sample t.
In this case the observations for sleep (in hours) are all in one column and the variable
sex (male or female) of the person is in another. Fill in the dialog boxes as shown below
and also check-off Assume equal variances.
The output is:
Two-Sample T-Test and CI: Sleep, Sex
Two-sample T for Sleep
Sex
Female
Male
N
83
65
Mean
7.02
6.55
StDev
1.75
1.68
SE Mean
0.19
0.21
Difference = mu (Female) - mu (Male)
Estimate for difference: 0.461214
95% CI for difference: (-0.102902, 1.025331)
T-Test of difference = 0 (vs not =): T-Value = 1.62
0.108 DF = 146
Both use Pooled StDev = 1.7233
P-Value =
In this case it was appropriate to use the ‘equal variance’ option because the standard
deviations (highlighted in red in the output) are very similar. If there is evidence (e.g.
previous studies, preliminary graphical analysis) that the variances are very different then
one should not mark the ‘equal variance’ option in the 2-Sample t window. Unequal
variance option is shown next.
140
Notice that now there is no ‘pooled’ estimate of the variance. Variances for each group
are estimated separately and then combined in the formula
s12 s 22
. Notice also that

n1 n 2
the number of degrees of freedom is no longer n1 + n2 - 2, rather the number of degrees
of freedom is calculated using the rather complicated formula shown in Section 12.5 of
the book.
Two-Sample T-Test and CI: Sleep, Sex
Two-sample T for Sleep
Sex
Female
Male
N
83
65
Mean
7.02
6.55
StDev
1.75
1.68
SE Mean
0.19
0.21
Difference = mu (Female) - mu (Male)
Estimate for difference: 0.461214
95% CI for difference: (-0.100180, 1.022608)
T-Test of difference = 0 (vs not =): T-Value = 1.62
0.107 DF = 140
P-Value =
Section 12.6 Computing a confidence interval for the difference of two proportions.
There are categorical variables that have only two possible categories, which can be
called ‘success’ and ‘failure.’ There are categorical variables that have several categories
that have been grouped into two. In this situation, attention is focused on the proportion
of elements of the population that fall in the category of ‘success.’ ‘Success’ can be
things like voting for candidate A, having a certain disease or answering ‘yes’ to a given
question in a survey. Sometimes there are two groups or populations that we want to
compare in terms of the proportion of the elements in each population that fall in the
141
category of success. This is the case of Example 12.10 ‘Snoring and Heart Attack’. We
will now show how to compute a confidence interval for the difference of proportions.
The data from the Snoring and Heart Attack example will be used.
Select Stat> Basic Statistics> 2 Proportions from the menu to obtain the following:
The first two options, Samples in one column and Samples in different columns, are used
for raw data, meaning a column formed only by zeros and ones (denoting ‘successes’ and
‘failures’, respectively). For example, if the data correspond to a survey, the value of the
variable would be 1 for those individuals who answered ‘Yes’ and 0 for those who
answered ‘No’.
The option Samples in one column is used when the values (0s and 1s) of the variable for
both groups are stacked in one column. Another column will be needed; one that
indicates to which group each individual (row) belongs.
The option Samples in different columns is used when the observations for each one of
the two groups are stored in two different columns, one for group 1 and the other for
group 2.
The third option, Summarized data, is used when the individual observations are not
available; rather, the number of success and failures has already been counted in each
group. This option will be shown below.
In Example 12.10 Snoring and Heart Attacks, two groups are being compared: snorers
and non-snorers. It was found that 86 out of 1105 snorers had heart disease while only 24
out of 1379 non-snorers had heart disease. In the book a formula is used to form
confidence intervals (90%, 95% and 99%) for the difference of population proportions
with heart disease for the two groups. Those calculations can also be done using Minitab.
Select Stat>Basic Statistics>2 Proportions from the menu and indicate the sample sizes
(Trials) and number of successes (Events) for each sample as shown below:
142
Click on Options to indicate the desired confidence level (90).
For 90% confidence, the output is:
Test and CI for Two Proportions
Sample
1
2
X
86
24
N
1105
1379
Sample p
0.077828
0.017404
Difference = p (1) - p (2)
Estimate for difference: 0.0604241
90% CI for difference: (0.0459577, 0.0748906)
Test for difference = 0 (vs not = 0): Z = 6.87
P-Value = 0.000
143
Those are the same values that appear rounded to three decimal places in Example 12.10
of the book. The same procedure, just changing the confidence, is applied to get the
other two confidence intervals (95% and 99%)
95% CI for p(1) - p(2):
99% CI for p(1) - p(2):
(0.0431863, 0.0776620)
(0.0377697, 0.0830786)
The intervals indicate that the proportion of snorers with heart disease is anywhere from
4% to 8% higher than the proportion of non-snorers with heart disease.
144