Download Chapter 5

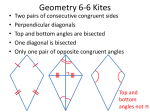
Chapter 5
5.1
Indirect Proof
An indirect proof is generally used when you need to prove something is not
true.
Suppose that you would like to prove two triangles are not congruent.
We have plenty of methods to prove they are congruent but none so far that
prove the opposite.
To solve Indirectly begin by Assuming the opposite of the prove is true. Use
this as if it is a given.
Reason until you reach a contradiction to a known geometric fact. This
could be a piece of given information or a rule we have already learned is
true.
When you reach this contradiction – state that your assumption is false and
therefore the prove statement must be true.
5.2
Proving Lines Parallel
In this section we will learn 7 methods for proving lines parallel but in order
to prove the first of these theorems we will need two other geometric
theorems.
Parts Theorem - The whole is greater than each of its parts.
This theorem is used whenever you want to state a segment or angle is
greater than the parts that add up to it.
Exterior angle of a triangle is formed by extending one side of the triangle. The
non adjacent angles in the interior of the triangle are referred to as the remote
interior angles for the exterior angle chosen.
ex. Name the remote interior angles in the figure for exterior <5
ans. < 3 and < 6
Exterior angle Theorem (EAT)- An exterior angle of a triangle is greater than
either of its remote interior angles.
There are seven methods of proving lines are parallel.
If the alternate interior angles are congruent, then the lines are parallel.
Proof.
Other methods of proving lines parallel.
If two lines are cut by a transversal and the corresponding angles are
congruent then the lines are parallel (CAP)
If two lines are cut by a transversal and the Alternate Exterior angles are
congruent, then the lines are parallel (AEP)
If two lines are cut by a transversal the the same-side interior angles are
supplementary, then the lines are parallel. (SSISP)
If two lines are cut by a transversal and the same-side exterior angles are
supplements, then the lines are parallel. (SSESP)
If 2 lines in a plane are both perpendicular to the same line then the lines are
parallel. (2P3P)
If two lines are both parallel to the same line then the lines are parallel.
(Trans of Parallel)
5.3 Congruent Angles Associated with Parallel Lines
Euclid's Parallel Postulate - Euclid thought this could be proven and the
postulate is quite famous among geometers in there effort to prove or
disprove. Some Non-Euclidean geometries are base on this being a false
postulate. We will accept this as true.
Through a point not on a line exactly one parallel to the given line can be
drawn.
Most of the theorems in this section are converses of the theorems learned in
5.2. In the previous section we learned that when specific pairs of angles
were congruent or supplementary then lines became parallel. In this section
we start with parallel lines and then state the special pairs of angles are
congruent or supplementary.
PAI - If two parallel lines are cut by a transversal, then the alternate interior
angles are congruent
PAE- If two parallel lines are cut by a transversal, then the alternate exterior
angles are congruent.
PCA- If two parallel lines are cut by a transversal, then the corresponding
angles are congruent.
PSSIS- If two parallel lines are cut by a transversal, then the same side interior
angles are supplements.
PSSES- If two parallel lines are cut by a transversal, then the same side
exterior angles are supplements.
Converse of 2P3P- If a transversal is perpendicular to one of two parallel lines,
then it is perpendicular to the other.
Example proof
5.4 4 sided Polygons
This section introduces us to the quadrilaterals which are 4 sided polygons.
Since polygon is a new word for us the section begins with a description of
what a polygon is, how to name a polygon, the difference between convex and
concave polygon and what a diagonal of a polygon is. I have also included in
this section the formula for finding the number of diagonals of a polygon.
Polygon
A polygon is a closed figure made by joining line segments, where each line
segment intersects exactly two others at one of their endpoints.
Examples: The following are examples of polygons:
The figure below is not a polygon, since it is not a closed figure:
The figure below is not a polygon, since it is not made of line segments:
The figure below is not a polygon, since its sides do not intersect in exactly two places
each:
When you name polygons name them by their vertices in consecutive order. The polygon below
is ABCDEF, CBAFED or any other combination as long as you stay in order, but you
cannot name in by skipping around BDCEFA is not a correct name for the figure
Diagonals are any segments in a polygon that connect non adjacent vertices.
The number of diagonals can be found by using the formula where n = number
of vertices of the polygon
diagonals = (n) (n-3)/2
Polygons are classified by their number of sides. We have already studied the
triangles and now begin our exploration of the 4 sided figures which are name
quadrilaterals.
Quadrilaterals - 4 sided polygons
The following are definitions of special quadrilaterals that have specific
properties.
Parallelogram Rectangle Rhombus
Square
Trapezoid
kite
a quadrilateral with both pair of opposite sides parallel
parallelogram with 4 right angles.
parallelogram with 4 congruent sides
parallelogram with 4 congruent sides and 4 congruent
angles
quadrilateral with exactly one pair of sides parallel.
quadrilateral with two pairs of disjoint congruent sides
Below is a diagram grouping the quadrilaterals. You will note that all
parallelograms are quadrilaterals.
All rectangles, squares and rhombuses are parallelograms. Some kites are
parallelograms ( when they are rhombuses) but the trapezoids belong to the
quadrilaterals but not the parallelograms. It is a bit confusing, but in the next
section we sort out all the properties and the diagram starts to make some
sense.
5.5 Properties of special quadrilaterals
Parallelogram - 5 Properties (POP)
Both pairs of opposite sides are parallel
Both pairs of opposite sides are congruent
Both pairs of opposite angles are congruent
Diagonals bisect each other
Consecutive angles are supplementary
Rectangle
All 5 properties of a parallelogram
4 right angles
Congruent diagonals
Rhombus
5 Properties of a Parallelogram
4 congruent sides
Perpendicular diagonals
Diagonals bisect the corner angles from which they are drawn
Square
5 Properties of a Parallelogram
2 Properties of a Rectangle
3 Properties of a Rhombus
Kite
Two disjoint pairs of consecutive sides are congruent
Diagonals are perpendicular bisectors of each other
One pair of opposite angles are congruent
One of the diagonals bisects the corner angles form which it is drawn
Isosceles Trapezoid
5.6 Methods of proving a quadrilateral is a parallelogram
5 methods of proving a quadrilateral is a parallelogram
1. Prove both pair of opposite sides parallel (Def. of a parallelogram)
2. Prove both pair of opposite sides congruent. (BSC)
3. Prove both pair of opposite angles congruent. (BAC)
4. Prove the diagonals bisect each other (DB)
5. Prove one pair of sides both congruent and parallel. (OPCP)
Tesselation of a modified parallelogram.
In sketchpad, use your parallelogram tool to draw a parallelogram and label the
vertices as below.
Holding down the shift key, choose points A and B in that order, and under the
transform menu, mark vector A B.
Using your segment tool draw a zigzag line starting at A and ending at D.
Select the segments and endpoints that you just drew (not including A and D)
and in transform choose translate. The zigzag line should appear on the top of
your parallelogram. Hide segments AD and BC.
Repeat the process by selecting A and D and under transform, mark vector
AD. Zigzag up from A to B. Choose your segments and points not including A
and B, tranlate them to the right side and hide segments AB and CD.
Choose every vertex consecutively around the figure. Don't skip over any or
jump around. Do not choose the segments. The under construct choose
polygon interior. This should fill in the polygon. Change to a pretty color.
Choose the polygon interior and translate it by vector AD 3 times. Alternate
your colors.
Mark vector B A by choosing first B then A and under transform, mark vector.
Then select the interior of your three shapes and translate them by this vector.
Translate the new row of vectors again by B A and alternate your colors.
Modify your original shape by dragging points. Make sure that your polygon
remains a polygon and the segments intersect only at their endpoints. Use your
imagination as to what your shape looks like and label your tesselation with a
text box including the title of your picture and your name. Send it too me in the
appropriate class folder or put it on your disk and leave the disk on my desk.