Download Here - BCIT Commons

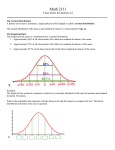
MATH 2441
Probability and Statistics for Biological Sciences
Measures of Variability
Measures of central tendency are designed to distinguish between two similar looking distributions of values
which are "centered" at different locations along the horizontal axis. In the figure on the left just below, the
two distributions of values have what appear to be identical or nearly identical shapes, but the location
around which their values seem most tightly clustered are different. The data sets from which these two
distribution graphs were created would give different means, medians, and modes.
0
2
4
6
8
0
2
4
6
On the other hand, the two data sets giving rise to the two distributions shown in the figure to the right above
will give the same values for any of those three measures of central tendency, yet they are clearly not
identical distributions of data. The peak, center, region of highest frequency, is around the value 4 for both,
but they differ in how spread out (or how variable, or how dispersed) the data values are.
These schematic examples suggest that a second numerical summary that might be a useful and distinctive
summary characteristic of data distributions is some measure of variability, or dispersion. We will
consider a few of the possible ways of quantifying the variability of data.
The Range
The simplest way to measure the spread of values in a set of data is to calculate the range:
sample range = largest value - smallest value
(VAR-1)
This has the advantage of being quite simple to do (though not necessarily very easy -- try scanning a list of
50,000 numbers by eye to find the largest and smallest values present). However, it suffers from the major
disadvantage that its value depends on the two most atypical numbers in the whole set of data. Not only is
the value of the range computed from just two observations, with all the other observations there just to tell
you which two to use in your calculation, but it is calculated from the two most unusual and unpredictable
values in the whole set of observations.
The range fails as a useful statistic in one other way. Remember that our goal in calculating numerical
summaries from sample data is to be able use them to say something about the population from which the
sample was selected. The question is: what population property might the sample range tell us about? For
the sample range to be a good estimate of the population range, it would have to happen that the sample
fortuitously contains both the smallest and the largest values occurring in the population. If the size of the
sample is small compared to the size of the population, then this is extremely unlikely.
Under some circumstances, the sample range can be used to get a rough estimate of the most commonly
used measure of dispersion, the standard deviation. See the document "Rough Cuts".
David W. Sabo (1999)
Measures of Variability
Page 1 of 5
8
The Mean Deviation
In sets of data with very little variability or spread, the individual data values will all tend to be very similar to
the arithmetic mean. This suggests that if we want to find a single number reflecting the spread or variability
of the data which takes into account all observations, perhaps it would be useful to consider something
based on the set of deviations from the mean: x1  x , x 2  x , x 3  x , …, x n  x . If most of the data
values, x1, x2, x3, …, xn, are near in value to the mean, x , then most of these deviations will be small values.
Instead, if there is quite a bit of variability in the data, at least some of these deviations will be quite large
values.
One might guess that simply finding the arithmetic mean of these deviations would be a good start.
Unfortunately, this doesn't work. To see why, note the following.
average deviation 
x1  x   x 2  x   x3  x     x n  x 
n
that is, add up all n deviations, and divide by n. Now, examine the numerator more closely. If the brackets
are removed, we can rearrange the terms to give the sum of the data values x1 + x2 + x3 + … + xn, and the
sum of x with itself n times, giving a total of n x . Thus, the right-hand side above can be rewritten as
average deviation 
x1  x 2  x 3    x n  nx x1  x 2  x 3    x n nx


 xx 0
n
n
n
Thus, the average deviation computed in this way will always give the answer zero, and so as a measure of
something to distinguish between narrow and broad distributions, it is totally useless. Note that we have
obtained with result without considering any specific data values -- it is a property of the way this average
deviation is defined that its value is automatically zero. In fact, you could say that the mean value, x , is the
value which makes the average deviation zero. What's really happening here is that the mean value has the
property that every unit of deviation to its right is balanced by an equivalent deviation to its left, so that when
you sum over all deviations, they exactly cancel out. Deviations of data values to the left of the mean will be
negative numbers, deviations of data values to the right of the mean will be positive values, and the positive
and negative values exactly cancel out.
The mean deviation was a good idea in that it took into account the values of all of the observations, but it
failed to be useful because of exact cancellation between positive and negative deviations. Some people
have suggested overcoming this difficulty by defining the mean absolute deviation -- take the absolute
value of each deviation averaging. This would prevent the cancellation of positive and negative values in
the averaging process, because now the sum involves only positive values.
n
mean absolute deviation 
 xk  x
k 1
n
(VAR-2)
Although this is used sometimes, the absolute value operation has some nasty mathematical properties (the
graph of the absolute value function has a kink at the origin) which limits its theoretical usefulness compared
to the next alternative we describe.
The Variance and Standard Deviation
There is another way to get a sum of strictly non-negative values based on deviations from the mean:
square the deviations before summing. This gives the so-called variance, which leads to the most
commonly used measure of variability in statistics. Since this quantity is going to work for us, we need to
take care now to distinguish between sample variance, s2, and population variance, 2. The notation is
conventional, and will make sense shortly. Here,  is the lower case Greek character "sigma" or "s", written
like an "o" with a short horizontal tail going rightwards from the top.
The defining formulas for these two quantities are:
Page 2 of 5
Measures of Variability
David W. Sabo (1999)
 x k  x 
n
s2 
2
 x k   
N
k 1
2 
and
n 1
2
k 1
(VAR-3)
N
Here, lower case n is the size of the sample, and upper case N is the size of the population. These two
formulas are similar in some respects: the numerator is the sum of the squares of the deviations from the
respective means. In calculating the sample variance, we sum the squares of the deviations of the data in
the sample from the sample mean. In computing the population variance, we would sum the squares of the
deviations of the values in the population from the population mean. To get an average of the deviations,
we should divide by the number of terms in the sum, as done in the formula for 2.
The explanation why the numerator in the formula for s 2 is n-1 instead of n is a bit subtle. One reason is that
we would like to be able to prove that as the sample size n increases until eventually the sample becomes
identical to the original population, the formula for s 2 should smoothly transition into the formula for 2. This
will only happen if we start with an n-1 in the denominator of the formula for s2. Another reason is that since
x has been calculated from the xk's in the sample, we really have only n-1 independent pieces of
information left. (If I give you the value of all but one observation plus the mean of all observations, you can
easily work out what that unknown observation must have been -- hence once x is known, one of the n
observations is redundant.) The value, n - 1, of the denominator of s2 is called the degrees of freedom in
this context.
Look closely at the two formulas, (VAR-3). If the data values tend to be close to the mean, then the
deviations from the mean will be a set of small numbers. Squaring them will give a set of small numbers,
and so the sum in the denominator will be a small number. Thus, for tightly clustered sets of data, s 2 is
expected to be a relatively small value. On the other hand, if the data values are widely spread out (or at
least if a few of them are), then some of the deviations will be large numbers and their squares will be even
larger numbers, leading to a relatively large value for the numerator and hence for s 2. Hence small values of
s2 indicate tightly clustered sets of data, whereas large values of s 2 indicate more spread in the distribution
of values.
The formulas (VAR-3) make it easy to see what features of the data are reflected by s 2 and 2, but they are
rather awkward formulas to use for actually calculating these quantities. We can rearrange the numerators
algebraically into the somewhat more congenial form:
n
s2 
 xk
2
k 1
 n

  xk 
 k 1 

n
n 1
2
n
2
2
 x k  nx
k 1

(VAR-4a)
n 1
and
N
2 
 xk
k 1
2
N 
  xk 
 k 1 

N
N
2
N

2
2
 x k  n
k 1
(VAR-4b)
N
The pattern of computations in the numerators of the first form in each of these formulas arises so
commonly in statistical calculations that it is often denoted by the symbol SS (we'll use the subscript labels
'sample' and 'pop' here to distinguish between the SS for the sample data and the SS for the population
values):
n
SS sample   x k 2
k 1
 n

  xk 
 k 1 

n
2
N
and
SS pop   x k 2
k 1
N 
  xk 
 k 1 

N
2
(VAR-5)
Then,
David W. Sabo (1999)
Measures of Variability
Page 3 of 5
s2 
SS sample
and
n 1
2 
SS pop
N
(VAR-6)
(Although we've given formulas for 2 throughout here, you will probably never calculate 2 directly, but will
use the value of s2 for data from a sample as an estimate of the required value of 2.)
Don't jump to the conclusion that the formula (VAR-5,6) for s2 is hopelessly complicated. To compute
SSsample, you just need the sum of the squares of the data values (the first term), and the sum of the data
values themselves (the second term). Even the simplest hand-held calculators with statistical functions will
automate the process of computing these sums for you. Note the distinction between the two terms in the
formula for SS. To compute the value of the first term you must square the values first, and then sum those
squares. In the second term, you first sum the values, and then square the sum. These are not the same
operations.
Before doing an example calculation, we define two more terms. The standard deviation is simply the
square root of the corresponding variance. Thus
sample standarddeviation  s  s 2
(VAR-7a)
population standarddeviation     2
(VAR-7b)
and
So, to compute the standard deviation, first compute the variance, and then take the square root. Obviously
the standard deviation reflects the same features of the data as does the variance. Large variances will
have comparatively large square roots, whereas small variances will have comparatively small square roots.
Thus a comparatively large value for the standard deviation is an indication of considerable variability in the
data, whereas a comparatively smaller value for the standard deviation is an indication of less variability in
the data.
Example: Biotin
To illustrate the use of the formulas, consider the 'BiotinDry' set of data:
58.70
91.40
78.00
80.90
88.40
96.10
97.40
104.80 78.20
BiotinDry
consisting of a sample of n = 9 values. To compute s2, start by computing
9
2
2
2
2
2
2
2
2
2
2
 x k  58 .70  78 .00  80 .90  88 .40  96 .10  97 .40  104 .80  78 .20  91 .40
k 1
= 68063.27
Also
9
 x k  58 .70  78 .00  80 .90  88 .40  96 .10  97 .40  104 .80  78 .20  91 .40  773 .90
k 1
Now, put it all together:
n
s2 
 xk
k 1
2
 n

  xk 
 k 1 

n
n 1
2
773 .90 2
9
 189 .559
9 1
68063 .27 

rounded to three decimal places. (Since the data values have units of micrograms/100 g peanuts, the units
of s2 will be the square of this.) Then,
s  s 2  189.559  13.768 g / 100 g peanuts
Page 4 of 5
Measures of Variability
David W. Sabo (1999)
If you applied the same procedure to the BiotinOil data, you would get s 2  9.667, and so s  3.109,
indicating that the values in this second set of data are much more tightly clustered about the mean than in
the BiotinDry data.

In practice, you should try to avoid having to calculate s 2 in as detailed a fashion as the above example
illustrates, especially for large sets of data. Using the statistical facilities on your hand-held calculator can
automate the process a bit. Be careful to distinguish between the function keys which calculate s 2 or s and
those which calculate 2 or . In Excel, the function STDEV() can be used to calculate s, and the functions
n
SUMSQ() and SUM() can be used to calculate  x k
k 1
2
n
and  x k , respectively.
k 1
As measures of dispersion, the variance and standard deviation have one major advantage: they arise
automatically in the theory underlying the sampling process, and so will play an important role in the
methods of statistical inference that will occupy most of the time in this course. s 2 is an efficient and
unbiased estimator of 2 (though the same is not quite true of the relationship between s and ). Their one
defect is shared with the arithmetic mean: the value of s2 and s is rather sensitive to the presence of
unusual or atypical observations.
The Interquartile Range
The interquartile range is a measure of dispersion based on the calculation of percentiles for the data.
Refer to the document on "Measures of Relative Standing" for further details. The main value of the
interquartile range is that it provides a measure of dispersion which is insensitive to the presence of a small
number of unusual or atypical observations. In some respects, you could consider the interquartile range to
play a similar role with respect to the median as the standard deviation does with respect to the mean.
The Coefficient of Variation
The so-called coefficient of variation, is defined as the ratio
CV 
s
x
(Var-8)
expressed either as a fraction or in percentage form. You can view it as a measure of relative dispersion or
relative variability. Recall that both s and x have the same units of measurement as the original data. If the
units of measurement are changed, the values of these quantities will change as well. Their ratio, CV, is
dimensionless, indicating how great the variability of the data is in relation to the value of the mean. CV's
only make sense for data measured relative to a ratio scale. However, in those instances it reflects how
significant variation between values is relative to their actual typical value.
For instance, if we collected a sample of 50 apples, and found that their mean weight was 300 g, a standard
deviation of 1 g would indicate a very uniform sample of apples, weightwise. (See the document "Rough
Cuts" -- the standard deviation of 1 g would indicate that almost all of the apples would have weights
between 297 g and 303 g.) On the other hand, if we collected a sample of 50 blueberries and found that
their mean weight was 1 g, a standard deviation of 1 g would indicate a quite a non-uniform set of
blueberries, with some being probably four - six times as large as others. In the first case, the very uniform
set of apples would have a CV of 1/300  0.003, and in the second case, the very diverse set of blueberries
would have a CV of 1/1 = 1 which is 300 times as big as the CV for the apples.
David W. Sabo (1999)
Measures of Variability
Page 5 of 5