Download Answers- Lines and slope

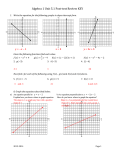
Practice Problems 2 - answers
Lines and Slope
Part I.
Forms of a linear relation.
a) Standard form or general form: Ax + By = C or Ax + By + C = 0
b) Slope-intercept form: y = mx + b
c) Intercept-form
x y
  1 where a= the x-intercept and b=the y=intercept
d)
a b
e) Point-slope form: y  y1  m( x  x1 )
f) Vertical line: x = h
g) Horizontal line: y = k
Find the slope of the following lines
1. The line that contains the points (0, 0) and (2, 1).
y  y1 1  0 1
slope  2


x 2  x1 2  0 2
2. The line containing the points (-2, 2), (1, 1).
y  y1 1  2  1
1
slope  2



x 2  x1 1  2 3
3
3. The line containing the points (2, 3), (4, 0).
y  y1 0  3  3
3
slope  2



x 2  x1 4  2 2
2
4. The line containing the points (-2, 3), (2, 1).
y  y1
1 3
2
1
slope  2



x 2  x1 2  2
4
2
5. The line containing the points (-3, -1), (2, -1).
y  y1  1  1 0
slope  2

  0, a horizontal line
x 2  x1
2  3 5
6. The line containing the points (-1, 2), (-1, -2).
y  y1  2  2  4
slope  2


 undefined , a vertical line
x 2  x1  1  1 0
-1-
Graph by hand (no calculator)
1. The line containing the point P=(1, 2) with slope m=3
3 3
m3 
means that y increases by 3 when x increases by 1
1 1
or y decreases by 3 when x decreases by 1.
Therefore the slope m generates the points (2, 5), (3, 8), (4, 11) or (0, -1), (-1, -4), (-2, -7)
y
x
Find the equation of the following lines
1. Containing the point P=(1, 2), with slope m=4
4 4
m4 
means that y increases by 4 when x increases by 1
1 1
or y decreases by 34 when x decreases by 1.
Therefore the slope m generates the po int s (2, 6), (3, 10), (4, 14), etc.
or (0,  2), (1,  6), (2,  10)
2. P=(2, -4), m  
3
2
3 3
3


means that y increases by 3 when x decreases by  2
2
2
2
or y decreases by 3 when x increases by 12.
m
Therefore the slope m generates the po int s (0,  1), (2, 2), (4, 5), etc.
or (4,  7), (6,  10), (8,  11)
3. The line containing the points (0, 0) and (2, 1)
y  y1 1  0 1
slope  2


x 2  x1 2  0 2
Use the po int slope form
 y 0 
y  y1  m( x  x1 )
1
1
( x  0)  y  x or
2
2
2 y  x or
-2-
x  2y  0
4. The line containing the points (-1, 3) and (1, 1)
y  y1 1  3  2
slope  2


 1
x 2  x1 1  1 2
Use the po int slope form
y  y1  m( x  x1 )  y  1  1( x  1)  y  1   x  1
y  x  2
or x  y  2
5. Slope =3; containing the point (-2, 3)
Use the po int slope form
y  y1  m( x  x1 )  y  3  3( x  2)  y  3  3x  6
y  3x  9 is the slope  int ercept form
or  3x  y  9 is the s tan dard or general form
6. Containing the points (1, 3) and (-1, 2)
y  y1
2  3 1 1
slope  2



x 2  x1  1  1  2 2
Use the po int slope form
y  y1  m( x  x1 )  y  3 
y
1
5
x
2
2
1
( x  1)  2 y  6  x  1
2
or  x  2 y  5
7. slope m=-3 and y-intercept=3
y= mx + b
y= -3x +3 or 3x + y=3
8. x-intercept = 2, y-intercept = -1
Therefore the line contains the points (2, 0) and (0, -1)
y  y1  1  0  1 1
slope  2



x 2  x1
02 2 2
Use the po int slope form
y  y1  m( x  x1 )  y  1 
y
1
x 1
2
1
1
( x  0)  y  1  x
2
2
or  x  2 y  2
-3-
9. Parallel to y=2x; containing the point (-1, 3)
The line we want has the same slope as y=2x because they are parallel.
Therefore we want a line with slope m=2, containing the point (-1, 3)
Use the po int slope form
y  y1  m( x  x1 )  y  3  2( x  1)  y  3  2 x  2
y  2 x  5 is the slope  int ercept form
or  2 x  y  5 is the s tan dard or general form
10. Parallel to the line 2x – y = -2; containing the point (0, 0)
The line 2x – y = -2 has slope m = 2. The line we are looking for has the same slope and
contains the point (0, 0)
Use the po int slope form
y  y1  m( x  x1 )  y  0  2( x  0)  y  2 x
y  2 x is the slope  int ercept form
or  2 x  y  0 or 2 x  y  0 is the s tan dard or general form
11. Parallel to the line x = 5 and containing the point (-1, 2).
The line x = 5 is a vertical line with no slope. Therefore the parallel line through (-1, 2) has no
slope and therefore has the equation x = -1.
12. Perpendicular to the line y 
1
x  4 ; containing the point (1, -2)
2
1
1
x  4 has slope m  . The slope of a perpendicular line is the negative
2
2
reciprocal and therefore has slope m = -2. The slope of the line we are looking for has slope
m=-2 and contains the point (1, -2)
Use the po int slope form
The line y 
y  y1  m( x  x1 )  y  2  2( x  1)  y  2  2 x  2
 y  2 x is the slope  int ercept form
or 2 x  y  0 is the s tan dard or general form
13. Perpendicular to the line x = 8; containing the point (3. 4)
The line x = 8 is a vertical line with no slope. The perpendicular line has to be horizontal with 0
slope. Therefore the desired line has equation y = 4.
-4-
14. Find the equation of the line perpendicular to the line 2x+y=2; containing the
point (-3, 0)
Solution:
Equation: y-y1 = m(x – x1)
The point (x1, y1) is the point (-3, 0)
2
The slope of 2x + y = 2 is
, therefore the slope of the line we are looking for has slope equal
1
1
to
because the slope of perpendicular lines are negative reciprocals.
2
1
Therefore the equation is given by y – 0 = (x- -3) or 2y = x+3 or -x + 2y =3
2
or x – 2y = -3
15. Find the equation of the line perpendicular to the line x - 2y=-5; containing the point
(0, 4)
Solution:
Equation: y-y1 = m(x – x1)
The point (x1, y1) is the point (0, 4)
1 1
 , therefore the slope of the line we are looking for has slope
The slope of x - 2y = -5 is
2 2
equal to  2 because the slope of perpendicular lines are negative reciprocals.
Therefore the equation is given by y – 4 = -2(x-0) or y - 4 = -2x or 2x + y =4
16. A car cost $20,000 and depreciates linearly at the rate of $3000 per year.
Find the equation of linear depreciation and the value of the car 5 years from now.
Solution:
y= mx + b is the equation of linear depreciation. b= 20,000 which is the value at x=0 years
(now). The slope is -3000/1 because the value goes down $3000 per year.
Therefore the equation of linear depreciation is y = -3000x + 20,000.
To find the value of the car 5 years from now input x=5 in the function and obtain
Y= -3000(5) + 20000 = $5000. Five years from now the value of the car is $5000.
17. Problem: Peter bought a car for $18000 knowing that it will depreciate to $3000 in 5 years.
a) What is the rate of linear depreciation?
a) __-$3000 per year___________
At time x = 0, the value is $18000, therefore the pair (0, 18000) belong to the linear relations\.
At time x = 5, the value is $3000, therefore the pair (5, 3000) belong to the linear relation.
3000  18000  15000
The rate of linear depreciation is m=

 30000 per year
5 0
5
b) What is the equation of the linear depreciation?
y = mx + b = -3000x + 18000
b) y = -3000x + 18000_
c) In how many years will the car have no value?
c) ___6 years__________
y = 0 when 0 = -3000x + 18000, that is 3000x = 18000, x =6 years
-5-
18. The Centigrade scale and the Fahrenheit scale are linearly related. Water freezes at
which is the same as 32  F and boils at 100  C which is the same as 212  F .
9
a) Find the linear equation that give F as a function of C
a) F  C  32 ____
5
We want F = f(C), therefore, we need point (C, F)
Consider the points (0, 32) and (100, 212)
0 C
The y-intercept is b = 32
212  32 180 9
The slope is m 


100  0 100 5
y  mx  b  F 
9
C  32
5
b) Find the linear equation that give C as a function of F
b) C 
5F  160
___
9
9
Solving F  C  32 for C we obtain 5F = 9C + 160, 5F – 160 = 9C
5
5F  160
C
9
100 F to C
5F  160 5(100)  160 500  160 340
C



 37.78C
9
9
9
9
c) Convert
d) Convert 40 C to F
9
9
F  C  32  (40)  32  72  32  104F
5
5
19. A four year old car has a value of $18000 and in 6 more years the value will be $600. If the
car depreciated linearly, what was the original price of the car?
Solution:
Consider the point (4, 18000) and (4+ 6, 600)
600  18000  17400

 $2900 per year
10  4
6
y  y 1  m( x  x1 )  y  18000  2900( x  4)
Slope m =
 y  18000  2900x  11600
 y  2900x  11600  18000
 y  2900x  29800
The original value of the car is the y-intercept = $29800
-6-
20 - Graph the region intersection of the inequalities 2x – 3y < 5 and 3x +4y >4
The line 2x – 3y = 5 contains the points (1, -1) and (4, 1)
The point (0, 0) belongs to the inequality 2x – 5y <5
The line 3x + 4y =4 contains the points (0, 1) and (4, -2)
The point (0, 0) does not belong to the inequality 3x + 4y >4
Solution is the intersection of the Red and Gree, that is the
blue region. between the lines.
x
-7-
Part II.
Equation y=mx +b
1) y 
3
x5
5
m=
2) f(x)= -2 x +3
y= -2x + 3
f ( x)  5 
3)
Slope m
1
x
2
1
y   x5
2
5) 3x + 2y = 10
6) 2x – 3y =12
7) 4x – 3f(x) –15=6
or 4x – 3y =21
8) 9 = 3 + 5x –2f(x)
or 5x – 2y =6
y-intercept b
B = -5
3
5
m=-2
B=3
B=5
1
2
m= 
 A 3

B
2
 A 2
m


B
3
 A 4
m


B
3
When x = 0, y = b = 5
m
m
2
3
4
3
 A 5 5


B
2 2
2
, y  int ercept (0, 4)
9
2
y  mx  b  y  x  4 or 9y  2x  36 or 2x  9y  36
9
9) m 
11) m  4, y  int ercept (0,  7)
y  mx  b  y  4x  7 or 4x  y  7
3
11) m  4.2 y  int e rce pt (0, )
4
3
y  mx  b  y  4.2x  or 4y  16.8x  3 or 16.8x  4y  3
4
or 168 x  40 y  30 or 84 x  20 y  15
2
, passe sthrough (3, 7 ). Use the po int  slope form
9
2
y  y1  m x  x1   y  7  x  3  9y  63  2x  6
9
2
57
 2x  9y  57 or y  x 
9
9
12 ) m 
-8-
B = -4
b=-7
B =-3
3
13) m   , passe sthrough ( 4,  1)
5
Use the po int slope form
3
y  y1  mx  x1   y  1   x  4   5y  5  3x  12
5
3
17
3x  5y  17 or y   x 
5
3
14. The line contains the points (-1, 5) and (2, -4)
slope 
y 2  y1  4  5  9


 3
x 2  x1
2  1
3
Use the po int slope form
y  y1  m( x  x1 )  y  5  3( x  1)  y  5  3 x  3
y  3x  2
or 3 x  y  2
15. The line contains the points (7, 0) and (-1, 4)
slope 
y 2  y1
40
4
1


  . Use the po int slope form
x 2  x1  1  7  8
2
1
y  y1  m( x  x1 )  y  0   ( x  7)  2 y   x  7
2
1
7
x  2 y  7 or y   x 
2
2
1

 x  2y  5  m   2
16. 
 The lines are parallel
 2x  4y  8  m   2   1
4
2

4

 y  4x  5  4x  y  5  m   1  4
17. 
 The lines are perpendicu lar
 4y  8  x  x  4y  8  m   1 

4
-9-
2
x 1
7
2
Parallel line : m  , po int  (3, 5)
7
Po int slope form : y  y 1  mx  x1 
18. (3, 5), y 
2
2
29
( x  3)  7y  35  2x  6  7y  2x  29  y  x 
7
7
7
7
Perpendicu lar line : m   , po int  (3, 5)
2
Po int slope form : y  y 1  mx  x1 
 y5
7
7
31
 y  5   ( x  3)  2y  10  7 x  21  2y  7x  31  y   x 
2
2
2
19. P=(1, 2), m=4
4 4
m4 
means that y increases by 4 when x increases by 1
1 1
or y decreases by 34 when x decreases by 1.
Therefore the slope m generates the po int s (2, 6), (3, 10), (4, 14), etc.
or (0,  2), (1,  6), (2,  10)
20. Perpendicular to the line x = 8; containing the point (3. 4)
The line x = 8 is a vertical line with no slope. The perpendicular line has to be horizontal with 0
slope. Therefore the desired line has equation y = 4.
21. P=(2, -4), m  
3
2
3 3
3


means that y increases by 3 when x decreases by  2
2
2
2
or y decreases by 3 when x increases by 12.
m
Therefore the slope m generates the po int s (0,  1), (2, 2), (4, 5), etc.
or (4,  7), (6,  10), (8,  11)
22. The line has the points (0, 0) and (2, 1)
y  y1 1  0 1
slope  2


x 2  x1 2  0 2
Use the po int slope form
 y 0 
y  y1  m( x  x1 )
1
1
( x  0)  y  x or
2
2
2 y  x or
-10-
x  2y  0
23. Parallel to the line 2x – y = -2; containing the point (0, 0)
The line 2x – y = -2 has slope m = 2. The line we are looking for has the same slope and
contains the point (0, 0)
Use the po int slope form
y  y1  m( x  x1 )  y  0  2( x  0)  y  2 x
y  2 x is the slope  int ercept form
or  2 x  y  0 or 2 x  y  0 is the s tan dard or general form
24. Parallel to the line x = 5 and containing the point (-1, 2).
The line x = 5 is a vertical line with no slope. Therefore the parallel line through (-1, 2) has no
slope and therefore has the equation x = -1.
1
x  4 ; containing the point (1, -2)
2
1
1
The line y  x  4 has slope m  . The slope of a perpendicular line is the negative
2
2
reciprocal and therefore has slope m = -2. The slope of the line we are looking for has slope
m=-2 and contains the point (1, -2)
Use the po int slope form
25. Perpendicular to the line y 
y  y1  m( x  x1 )  y  2  2( x  1)  y  2  2 x  2
 y  2 x is the slope  int ercept form
or 2 x  y  0 is the s tan dard or general form
-11-