Download chapter 2 - WordPress.com

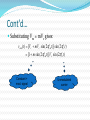
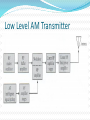
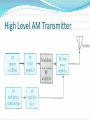
AMPLITUDE MODULATION
(AM)
Objectives
 To describe the principles of AM
 To define and analyze the modulation index
 To analyze the spectral analysis and bandwidth
calculation
 To analyze the power distribution of AM
Lecture overview
 Principles of amplitude modulation (AM)
 Modulation index
 Spectral analysis and bandwidth calculation
 Power analysis of AM
Principles of AM
 Definitions:
 The process of changing the amplitude of a
relatively high frequency carrier signal in
proportion with the instantaneous value of
modulating signal (information)
 A process of translating information signal from
low band frequency to high band
frequency.
Cont’d…
 Information signal cannot travel far. It needs carrier
signal of higher frequency for long distance
destination.
 Inexpensive, low quality form of modulation
Cont’d…
 Amplitude of the carrier signal varies with the
information signal.
 The modulated signal consist of carrier signal,
upper sideband and lower sideband signals
 The modulated AM signal (figure 1 & figure 2)
needs to go through demodulation process to get
back the information signal.
Cont’d…
The AM Envelope
 AM double-sideband full carrier (AM DSBFC) is
the most commonly used and the oldest and
simplest form of AM modulation.
 Sometimes called conventional AM or simply AM.
 The outline of the positive and negative peaks of
the carrier frequency re-create the exact shape of
the modulating signal known as envelope.
 Note that the repetition rate of the envelope is
equal to the frequency of the modulating signal.
The Generation of AM Envelope
AM Frequency Spectrum and Bandwidth
 An AM modulator is a non-linear device.
 Nonlinear mixing results in a complex output
envelope consists of the carrier frequency and the
sum (fc + fm) and difference (fc – fm) frequencies
(called cross-products).
 The cross-products are displaced from the carrier
frequency by fm on both sides of it.
 AM modulated wave contains no frequency
component of fm.
Frequency spectrum of an AM DSBFC Wave
Bandwidth (BW)
 The BW of an AM DSBFC wave is equal to the
difference between the highest upper side frequency
and lowest lower side frequency:
 BW = [fc + fm(max)] – [fc – fm(max)]
= 2fm(max)
 For efficiency transmission the carrier and sidebands
must be high enough to be propagated thru earth’s
atmosphere.
Example 1

a)
b)
c)
d)
For a conventional AM modulator with a carrier
freq of fc = 100 kHz and the maximum
modulating signal frequency of fm(max = 5 kHz,
determine:
Freq limits for the upper and lower sidebands.
Bandwidth.
Upper and lower side frequencies produced
when the modulating signal is a single-freq 3kHz tone.
Draw the output freq spectrum.
Modulation Index and Percent of
Modulation
 Used to describe the amount of amplitude change
(modulation) present in an AM waveform.
 Percentage modulation (%m) is simply the
modulation index (m) stated as a percentage.
 More specifically percent modulation gives the
percentage change in the amplitude of the output
wave when the carrier is acted on by a modulating
signal.
Cont’d…
 Mathematically, the modulation index is
m = modulation index
m
Em = peak change in the amplitude output
waveform (sum of voltages from upper and
lower side frequencies)
E
E
m
c
Ec = peak amplitude of the unmodulated
carrier
 And the percentage of modulation index is
E
%m
x 100%
E
m
c
Determining modulation index from Vmax
and Vmin
Cont’d…
 If the modulating signal is a pure, single-freq sine
wave and the process is symmetrical then the
modulation index can be derived as follows:
1
(V  V )
2
1
E  (V  V )
2
E 
 Therefore,
m
max
c
max
min
min
1
(Vmax  Vmin )
(V  Vmin )
2
m
 max
1
(Vmax  Vmin )
(Vmax  Vmin )
2
Cont’d…
 Since the peak change of modulated output
wave Em is the sum of the usf and lsf voltages
hence,
E E E
m
usf
where E  E
lsf
usf
 Then
1
(V  V )
E
E E 
2
2
2
1
 (V  V )
4
max
min
lsf
Eusf = peak amplitude
of the upperside
frequency (volts)
m
usf
lsf
max
min
Elsf = peak amplitude
of the lower side
frequency (volts)
Cont’d…
 From the modulated wave displayed in the previous
slide, the maximum and minimum values of the
envelope occurs at
+Vmax = Ec + Eusb + Elsb
+Vmin = Ec – Eusb – Elsb
-Vmax = -Ec - Eusb - Elsb
-Vmin = -Ec + Eusb + Elsb
Modulation Index for
trapezoidal patterns
 Modulation index, m can be calculated using
the equation:
m = Emax – Emin/ Emax + Emin
= Em / Ec
= (A - B) / (A + B)
Cont’d…
% modulation of AM DSBFC envelope
Cont’d…
 For proper AM operation, Ec > Em means that 0≤ m ≤ 1.
 If Ec < Em means that m > 1 leads to severe distortion of
the modulate wave.
 If Vc = Vm the percentage of modulation index goes to
100%, means the maximum information signal is
transmitted. In this case, Vmax = 2Vc and Vmin = 0.
Example 2
 Suppose that Vmax value read from the graticule on an
oscilloscope screen is 4.6 divisions and Vmin is 0.7
divisions. Calculate the modulation index and
percentage of modulation.
Example 3

a)
b)
c)
d)
e)
For the AM waveform shown in Figure below,
determine
Peak amplitude of the upper and lower side
frequencies.
Peak amplitude of the unmodulated carrier.
Peak change in the amplitude of the envelope.
Modulation index.
Percent modulation.
AM Envelope for Example 3
The Mathematical Representation
and Analysis of AM
 Representing both the modulating signal Vm(t) and the
carrier signal Vc(t) in trigonometric functions.
 The AM DSBFC modulator must be able to produce
mathematical multiplication of these two analog signals
v m (t )  Vm sin (2f m t )
v am (t )  [Vc  Vm sin (2f m t )] sin (2f c t )
vc (t )  Vc sin (2f c t )
Cont’d…
 Substituting Vm = mVc gives:
v am (t )  [Vc  mVc sin (2f m t )] sin (2f c t )
 [1  m sin (2f m t )] Vc sin (2f c t )
Constant +
mod. signal
Unmodulated
carrier
Cont’d…
 The constant in the first term produces the carrier freq
while the sinusoidal component in the first term
produces side bands frequencies
v (t )  V sin (2f t )  [mV sin (2f t )] [sin (2f t )]
am
c
c
c
 V sin (2f t ) 
c
Carrier frequency
signal (volts)

c
m
c
mV
cos [2 ( f  f )t ]
2
c
c
mV
cos [2 ( f  f )t ]
2
m
c
c
m
Lower side frequency
signal (volts)
Upper side frequency
signal (volts)
Cont’d…
 From the equation it is obvious that the amplitude of
the carrier is unaffected by the modulation process.
 The amplitude of the side frequencies depend on the
both the carrier amplitude and modulation index.
 At 100% modulation the amplitudes of side
frequencies are each equal to one-half the amplitude
of the carrier.
Generation of AM DSBFC envelope showing
the time-domain of the modulated wave,
carrier&sideband signals
Voltage spectrum for an AM DSBFC wave
Example 4

a)
b)
c)
d)
e)
One input to a conventional AM modulator is a 500-kHz
carrier with an amplitude of 20 Vp. The second input is a
10-kHz modulating signal that is of sufficient amplitude
to cause a change in the output wave of ±7.5 Vp.
Determine
Upper and lower side frequencies.
Modulation index and percentage modulation.
Peak amplitude of the modulated carrier and the upper
and lower side frequency voltages.
Maximum and minimum amplitudes of the envelope.
Expression for the modulated wave.
AM Power Distribution
 In any electrical circuit, the power dissipated
is equal to the voltage squared (rms) divided
by the resistance.
 Mathematically power in unmodulated carrier
is
2
2
Pc 
(Vc / 2 )
V
 c
R
2R
Pc = carrier power (watts)
Vc = peak carrier voltage (volts)
R = load resistance i.e antenna (ohms)
Cont’d
 The upper and lower sideband powers will
be
2
2
2
(mV c / 2)
m Vc
Pus b  Plsb 

2R
8R
 Rearranging in terms of Pc,
2
2 
m  Vc  m 2
Pus b  Plsb 

P
c


4  2R 
4
Cont’d…
 The total power in an AM wave is
Pt  Pc  Pusb  Plsb
 Substituting the sidebands powers in terms of PC yields
m2
m2
Pt  Pc 
Pc 
Pc
4
4
m2
m2
 Pc 
Pc  Pc [1 
]
2
2
 Since carrier power in modulated wave is the same as
unmodulated wave, obviously power of the carrier is
unaffected by modulation process.
Power spectrum for AM DSBFC wave with a
single-frequency modulating signal
Cont’d…
 With 100% modulation the maximum power in
both sidebands equals to one-half the carrier
power.
 One of the most significant disadvantage of AM
DSBFC is with m = 1, the efficiency of transmission
is only 33.3% of the total transmitted signal. The
less wasted in the carrier which brings no
information signal.
 The advantage of DSBFC is the use of relatively
simple, inexpensive demodulator circuits in the
receiver.
Example 5

For an AM DSCFC wave with a peak unmodulated
carrier voltage Vc = 10 Vp, a load resistor of RL = 10 
and m = 1, determine
a) Powers of the carrier and the upper and lower
sidebands.
b) Total sideband power.
c) Total power of the modulated wave.
d) Draw the power spectrum.
Transmitter Efficiency
Transmitter efficiency,
‫ = תּ‬average power from sideband/total
absorbed.
= m²/ ( 2+m² )
power
Modulation by a complex
information signal
 Previous examples are all using a single frequency modulation signal.
In practice, however, modulating signal is very often a complex
waveform made up from many sine waves with different amplitudes
and frequencies.
 Example: if a modulating signal contains three frequencies(fm1, fm2,
fm3), the modulated signal will contain the carrier and three sets of side
frequencies, spaced symmetrically about the carrier:
mV
mV
mV
cos [2 ( f  f )t ] 
cos [2 ( f  f )t ] 
cos [2 ( f  f )t ]
2
2
2
mV
mV
mV

cos [2 ( f  f )t ] 
cos [2 ( f  f )t ] 
cos [2 ( f  f )t ]
2
2
2
v (t )  V sin (2f t ) 
am
c
c
c
c
c
c
c
m1
c
c
c
m2
m1
c
c
c
m3
c
m3
m2
Cont’d..frequency spectrum for
complex information signal
Fc-fm3
Fc-fm2
Fc-fm1
fc
Fc+fm1 Fc+fm2 Fc+fm3
Cont’d..modulation index for
complex information signal
 When several frequencies simultaneously
amplitude modulate a carrier, the combined
coefficient of modulation is defined as:
m  m  m  m  ...  m
t
2
2
2
2
1
2
3
n
mt=total modulation index/coefficient of modulation
m1, m2, m3, mn= modulation index/coefficient of modulation
for input 1, 2 ,3 , n
Cont’d..Power calculation for complex
information signal
 The combined coefficient of modulation can be used
to determine the total sideband power and transmitted
power, using:
Pm
P P 
4
Pm
P 
2
m 

P  P 1 

2 

2
c
usbt
t
lsbt
2
c
t
sbt
2
t
t
c
Example 6

For an AM DSBFC transmitter with an unmodulated carrier power,
Pc= 100W that is modulated simultaneously by three modulating
signals, with coefficients of modulation m1=0.2, m2= 0.4, m3=0.3,
determine:
a)
Total coefficient of modulation
Upper and lower sideband power
Total transmitted power
b)
c)
Low Level AM Transmitter
High Level AM Transmitter
At the end of this chapter, you
should be able
 To describe the principles of AM
 To define and analyze the modulation index
 To analyze the spectral analysis and bandwidth
calculation
 To analyze the power distribution of AM