Download Can Renormalization Change the Observable Predictions of Inflation? Gonzalo J. Olmo

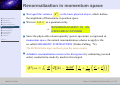
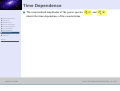
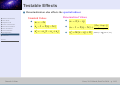
Can Renormalization Change the Observable
Predictions of Inflation?
Gonzalo J. Olmo
Instituto de Estructura de la Materia - CSIC (Spain)
In collaboration with I.Agullo, J.Navarro-Salas, and L.Parker
Gonzalo J. Olmo
Motivation and Summary
■
● Motivation and Summary
Inflation provides a natural solution to the horizon and flatness problems
of the hot Big Bang cosmology.
● Tensor Modes
● Amplitude of TM
● Need for renormalization
● Renormalization Method
● Tensor Perturbations
● Scalar Perturbations
● Time Dependence
● Testable Effects
● Conclusions
The End
Gonzalo J. Olmo
Porto, 29-31 March, IberiCos 2010 - p. 2/13
Motivation and Summary
■
Inflation provides a natural solution to the horizon and flatness problems
of the hot Big Bang cosmology.
■
Inflation also provides a Quantum Mechanical mechanism to account for
the origin of small inhomogeneities in the early Universe, which represent
the seeds for structure formation.
● Motivation and Summary
● Tensor Modes
● Amplitude of TM
● Need for renormalization
● Renormalization Method
● Tensor Perturbations
● Scalar Perturbations
● Time Dependence
● Testable Effects
● Conclusions
The End
Gonzalo J. Olmo
Porto, 29-31 March, IberiCos 2010 - p. 2/13
Motivation and Summary
■
Inflation provides a natural solution to the horizon and flatness problems
of the hot Big Bang cosmology.
■
Inflation also provides a Quantum Mechanical mechanism to account for
the origin of small inhomogeneities in the early Universe, which represent
the seeds for structure formation.
■
A relic background of gravitational waves is also unavoidable if inflation
happened in the early Universe.
● Motivation and Summary
● Tensor Modes
● Amplitude of TM
● Need for renormalization
● Renormalization Method
● Tensor Perturbations
● Scalar Perturbations
● Time Dependence
● Testable Effects
● Conclusions
The End
Gonzalo J. Olmo
Porto, 29-31 March, IberiCos 2010 - p. 2/13
Motivation and Summary
■
Inflation provides a natural solution to the horizon and flatness problems
of the hot Big Bang cosmology.
■
Inflation also provides a Quantum Mechanical mechanism to account for
the origin of small inhomogeneities in the early Universe, which represent
the seeds for structure formation.
■
A relic background of gravitational waves is also unavoidable if inflation
happened in the early Universe.
■
Typically, an inflationary model predicts the value of 3 parameters:
ns −1
◆ Scalar spectral index ns ⇒ Ps (k) = Ps (k0 ) k
k0
● Motivation and Summary
● Tensor Modes
● Amplitude of TM
● Need for renormalization
● Renormalization Method
● Tensor Perturbations
● Scalar Perturbations
● Time Dependence
● Testable Effects
● Conclusions
The End
Gonzalo J. Olmo
◆
Tensor spectral index nt ⇒ Pt (k) = Pt (k0 )
◆
Tensor-to-scalar ratio r ⇒ r ≡
nt
k
k0
Pt
Ps
Porto, 29-31 March, IberiCos 2010 - p. 2/13
Motivation and Summary
■
Inflation provides a natural solution to the horizon and flatness problems
of the hot Big Bang cosmology.
■
Inflation also provides a Quantum Mechanical mechanism to account for
the origin of small inhomogeneities in the early Universe, which represent
the seeds for structure formation.
■
A relic background of gravitational waves is also unavoidable if inflation
happened in the early Universe.
■
Typically, an inflationary model predicts the value of 3 parameters:
ns −1
◆ Scalar spectral index ns ⇒ Ps (k) = Ps (k0 ) k
k0
● Motivation and Summary
● Tensor Modes
● Amplitude of TM
● Need for renormalization
● Renormalization Method
● Tensor Perturbations
● Scalar Perturbations
● Time Dependence
● Testable Effects
● Conclusions
The End
■
Gonzalo J. Olmo
◆
Tensor spectral index nt ⇒ Pt (k) = Pt (k0 )
◆
Tensor-to-scalar ratio r ⇒ r ≡
nt
k
k0
Pt
Ps
These parameters are not independent.
Porto, 29-31 March, IberiCos 2010 - p. 2/13
Motivation and Summary
■
Inflation provides a natural solution to the horizon and flatness problems
of the hot Big Bang cosmology.
■
Inflation also provides a Quantum Mechanical mechanism to account for
the origin of small inhomogeneities in the early Universe, which represent
the seeds for structure formation.
■
A relic background of gravitational waves is also unavoidable if inflation
happened in the early Universe.
■
Typically, an inflationary model predicts the value of 3 parameters:
ns −1
◆ Scalar spectral index ns ⇒ Ps (k) = Ps (k0 ) k
k0
● Motivation and Summary
● Tensor Modes
● Amplitude of TM
● Need for renormalization
● Renormalization Method
● Tensor Perturbations
● Scalar Perturbations
● Time Dependence
● Testable Effects
● Conclusions
The End
Gonzalo J. Olmo
◆
Tensor spectral index nt ⇒ Pt (k) = Pt (k0 )
◆
Tensor-to-scalar ratio r ⇒ r ≡
nt
k
k0
Pt
Ps
■
These parameters are not independent.
■
Consistency condition for (single-field) slow roll inflation: r ≡ −8nt
Porto, 29-31 March, IberiCos 2010 - p. 2/13
Motivation and Summary
■
So far, observations just provide upper limits on tensor fluctuations.
● Motivation and Summary
● Tensor Modes
● Amplitude of TM
● Need for renormalization
● Renormalization Method
● Tensor Perturbations
● Scalar Perturbations
● Time Dependence
● Testable Effects
● Conclusions
The End
Gonzalo J. Olmo
Porto, 29-31 March, IberiCos 2010 - p. 3/13
Motivation and Summary
● Motivation and Summary
● Tensor Modes
● Amplitude of TM
● Need for renormalization
● Renormalization Method
● Tensor Perturbations
■
So far, observations just provide upper limits on tensor fluctuations.
■
Forthcoming high-precision measurements may detect effects of relic
gravitational waves and offer a test of the consistency condition
r ≡ −8nt
● Scalar Perturbations
● Time Dependence
● Testable Effects
● Conclusions
The End
Gonzalo J. Olmo
Porto, 29-31 March, IberiCos 2010 - p. 3/13
Motivation and Summary
● Motivation and Summary
■
So far, observations just provide upper limits on tensor fluctuations.
■
Forthcoming high-precision measurements may detect effects of relic
gravitational waves and offer a test of the consistency condition
r ≡ −8nt
■
If observations determine that r 6= −8nt then single-field slow roll
inflation would be ruled out !!!
● Tensor Modes
● Amplitude of TM
● Need for renormalization
● Renormalization Method
● Tensor Perturbations
● Scalar Perturbations
● Time Dependence
● Testable Effects
● Conclusions
The End
Gonzalo J. Olmo
Porto, 29-31 March, IberiCos 2010 - p. 3/13
Motivation and Summary
● Motivation and Summary
■
So far, observations just provide upper limits on tensor fluctuations.
■
Forthcoming high-precision measurements may detect effects of relic
gravitational waves and offer a test of the consistency condition
r ≡ −8nt
■
If observations determine that r 6= −8nt then single-field slow roll
inflation would be ruled out !!!
● Tensor Modes
● Amplitude of TM
● Need for renormalization
● Renormalization Method
● Tensor Perturbations
● Scalar Perturbations
● Time Dependence
● Testable Effects
● Conclusions
The End
We shall argue that Quantum Field Renormalization significantly influences the predictions of primordial perturbations
and hence the expected measurable imprint of inflation on the
CMB. In particular, we will find a new consistency condition:
q
′
4nt
r = 4(1−ns −nt )+ n2 −2n
1 − ns − 2nt′ + (1 − ns )2 − nt′ 2
′
t
Gonzalo J. Olmo
t
Porto, 29-31 March, IberiCos 2010 - p. 3/13
Motivation and Summary
● Motivation and Summary
■
So far, observations just provide upper limits on tensor fluctuations.
■
Forthcoming high-precision measurements may detect effects of relic
gravitational waves and offer a test of the consistency condition
r ≡ −8nt
■
If observations determine that r 6= −8nt then single-field slow roll
inflation would be ruled out !!!
● Tensor Modes
● Amplitude of TM
● Need for renormalization
● Renormalization Method
● Tensor Perturbations
● Scalar Perturbations
● Time Dependence
● Testable Effects
● Conclusions
The End
We shall argue that Quantum Field Renormalization significantly influences the predictions of primordial perturbations
and hence the expected measurable imprint of inflation on the
CMB. In particular, we will find a new consistency condition:
q
′
4nt
r = 4(1−ns −nt )+ n2 −2n
1 − ns − 2nt′ + (1 − ns )2 − nt′ 2
′
t
■
Gonzalo J. Olmo
t
I will try to justify why renormalization is needed and how it affects
the predictions of single field slow roll inflation.
Porto, 29-31 March, IberiCos 2010 - p. 3/13
Tensorial Perturbations. Standard Approach.
■
● Motivation and Summary
● Tensor Modes
● Amplitude of TM
● Need for renormalization
● Renormalization Method
Consider the fluctuating tensorial modes hi j (~x,t) , where
gi j = a2 (t)(δi j + hi j )
and a(t) is the expansion factor in the background
metric ds2 = −dt 2 + a2 (t)d~x2 .
● Tensor Perturbations
● Scalar Perturbations
● Time Dependence
● Testable Effects
● Conclusions
The End
Gonzalo J. Olmo
Porto, 29-31 March, IberiCos 2010 - p. 4/13
Tensorial Perturbations. Standard Approach.
■
Consider the fluctuating tensorial modes hi j (~x,t) , where
gi j = a2 (t)(δi j + hi j )
● Motivation and Summary
● Tensor Modes
and a(t) is the expansion factor in the background
metric ds2 = −dt 2 + a2 (t)d~x2 .
● Amplitude of TM
● Need for renormalization
● Renormalization Method
● Tensor Perturbations
● Scalar Perturbations
● Time Dependence
● Testable Effects
● Conclusions
The End
Gonzalo J. Olmo
■
The perturbation field hi j can be decomposed into two polarization states
both obeying the wave equation
ḧ + 3H ḣ − a−2 ∇2 h = 0
Porto, 29-31 March, IberiCos 2010 - p. 4/13
Tensorial Perturbations. Standard Approach.
■
Consider the fluctuating tensorial modes hi j (~x,t) , where
gi j = a2 (t)(δi j + hi j )
● Motivation and Summary
● Tensor Modes
and a(t) is the expansion factor in the background
metric ds2 = −dt 2 + a2 (t)d~x2 .
● Amplitude of TM
● Need for renormalization
● Renormalization Method
● Tensor Perturbations
● Scalar Perturbations
■
● Time Dependence
● Testable Effects
● Conclusions
The End
■
Gonzalo J. Olmo
The perturbation field hi j can be decomposed into two polarization states
both obeying the wave equation
ḧ + 3H ḣ − a−2 ∇2 h = 0
In slow roll inflation (ε ≡ −Ḣ/H 2 ≪ 1) the form of the modes is
q
16πGτπ i~k~x (1)
H3/2+ε (−kτ)
h~k (~x,t) = − 4(2π)
3 a2 e
Porto, 29-31 March, IberiCos 2010 - p. 4/13
Tensorial Perturbations. Standard Approach.
■
Consider the fluctuating tensorial modes hi j (~x,t) , where
gi j = a2 (t)(δi j + hi j )
● Motivation and Summary
● Tensor Modes
and a(t) is the expansion factor in the background
metric ds2 = −dt 2 + a2 (t)d~x2 .
● Amplitude of TM
● Need for renormalization
● Renormalization Method
● Tensor Perturbations
● Scalar Perturbations
■
● Time Dependence
● Testable Effects
● Conclusions
The End
Gonzalo J. Olmo
The perturbation field hi j can be decomposed into two polarization states
both obeying the wave equation
ḧ + 3H ḣ − a−2 ∇2 h = 0
■
In slow roll inflation (ε ≡ −Ḣ/H 2 ≪ 1) the form of the modes is
q
16πGτπ i~k~x (1)
H3/2+ε (−kτ)
h~k (~x,t) = − 4(2π)
3 a2 e
■
In pure de Sitter (ε = 0) the modes take the simple form
q
−1 −Ht
~
h~k (~x,t) = π2Gk3 (H − ike−Ht )eik~x eikH e
Porto, 29-31 March, IberiCos 2010 - p. 4/13
Amplitude of Tensorial Perturbations
■
At early times, the amplitude of oscillations depends on k/a(t) in a way
similar to that of a massless field in Minkowski space.
● Motivation and Summary
● Tensor Modes
● Amplitude of TM
● Need for renormalization
● Renormalization Method
● Tensor Perturbations
● Scalar Perturbations
● Time Dependence
● Testable Effects
● Conclusions
The End
Gonzalo J. Olmo
Porto, 29-31 March, IberiCos 2010 - p. 5/13
Amplitude of Tensorial Perturbations
■
At early times, the amplitude of oscillations depends on k/a(t) in a way
similar to that of a massless field in Minkowski space.
■
As time evolves, the physical wavelength reaches the Hubble radius when
t = tk ⇒ k/a(tk ) = H(tk )
● Motivation and Summary
● Tensor Modes
● Amplitude of TM
● Need for renormalization
● Renormalization Method
● Tensor Perturbations
● Scalar Perturbations
● Time Dependence
● Testable Effects
● Conclusions
The End
Gonzalo J. Olmo
Porto, 29-31 March, IberiCos 2010 - p. 5/13
Amplitude of Tensorial Perturbations
■
At early times, the amplitude of oscillations depends on k/a(t) in a way
similar to that of a massless field in Minkowski space.
■
As time evolves, the physical wavelength reaches the Hubble radius when
t = tk ⇒ k/a(tk ) = H(tk )
■
A few Hubble times after horizon exit (−kτ ≈ 1) the amplitude freezes to
● Motivation and Summary
● Tensor Modes
● Amplitude of TM
● Need for renormalization
● Renormalization Method
● Tensor Perturbations
● Scalar Perturbations
● Time Dependence
● Testable Effects
● Conclusions
The End
Gonzalo J. Olmo
the constant value |hk
|2
=
GH(tk )2
π2 k3
Porto, 29-31 March, IberiCos 2010 - p. 5/13
Amplitude of Tensorial Perturbations
■
At early times, the amplitude of oscillations depends on k/a(t) in a way
similar to that of a massless field in Minkowski space.
■
As time evolves, the physical wavelength reaches the Hubble radius when
t = tk ⇒ k/a(tk ) = H(tk )
■
A few Hubble times after horizon exit (−kτ ≈ 1) the amplitude freezes to
● Motivation and Summary
● Tensor Modes
● Amplitude of TM
● Need for renormalization
● Renormalization Method
● Tensor Perturbations
● Scalar Perturbations
● Time Dependence
● Testable Effects
the constant value |hk
● Conclusions
The End
■
|2
=
GH(tk )2
π2 k3
The freezing amplitude is usually codified through the quantity ∆2h (k,t) ,
defined in general by ∆2h = 4πk3 |h~k |2 and evaluated at the horizon
crossing time tk (or a few Hubble times after it).
Gonzalo J. Olmo
Porto, 29-31 March, IberiCos 2010 - p. 5/13
Amplitude of Tensorial Perturbations
■
At early times, the amplitude of oscillations depends on k/a(t) in a way
similar to that of a massless field in Minkowski space.
■
As time evolves, the physical wavelength reaches the Hubble radius when
t = tk ⇒ k/a(tk ) = H(tk )
■
A few Hubble times after horizon exit (−kτ ≈ 1) the amplitude freezes to
● Motivation and Summary
● Tensor Modes
● Amplitude of TM
● Need for renormalization
● Renormalization Method
● Tensor Perturbations
● Scalar Perturbations
● Time Dependence
● Testable Effects
the constant value |hk
● Conclusions
The End
■
|2
=
GH(tk )2
π2 k3
The freezing amplitude is usually codified through the quantity ∆2h (k,t) ,
defined in general by ∆2h = 4πk3 |h~k |2 and evaluated at the horizon
crossing time tk (or a few Hubble times after it).
■
One finally obtains a nearly “scale free” tensorial power spectrum
2
H(t
)
k
Pt (k) ≡ 4∆2h = M82
2π
P
√
where MP = 1/ 8πG is the reduced Planck mass.
Gonzalo J. Olmo
Porto, 29-31 March, IberiCos 2010 - p. 5/13
Need for renormalization: variance of h(~x,t).
■
● Motivation and Summary
● Tensor Modes
In position space, the variance of the tensorial perturbations is defined as
R 3
R ∞ dk 2
2
2
~
hh i = d k|h~ (~x,t)| =
∆ (k)
k
0
k
h
● Amplitude of TM
● Need for renormalization
● Renormalization Method
● Tensor Perturbations
● Scalar Perturbations
● Time Dependence
● Testable Effects
● Conclusions
The End
Gonzalo J. Olmo
Porto, 29-31 March, IberiCos 2010 - p. 6/13
Need for renormalization: variance of h(~x,t).
■
k
● Motivation and Summary
● Tensor Modes
● Amplitude of TM
● Need for renormalization
● Renormalization Method
● Tensor Perturbations
● Scalar Perturbations
● Time Dependence
● Testable Effects
● Conclusions
In position space, the variance of the tensorial perturbations is defined as
R 3
R ∞ dk 2
2
2
~
hh i = d k|h~ (~x,t)| =
∆ (k)
■
0
k
h
Due to the large k behavior of the modes the above integral is divergent:
i
R ∞ dk 16πGk3 h a
(2+3ε)
2
hh (~x,t)i = 0 k 4π2 a3 k [1 + 2k2 τ2 ] + ...
◆
◆
First term: quadratic divergence (typical in Minkowski).
Second term: logarithmic divergence (typical in expanding universe).
The End
Gonzalo J. Olmo
Porto, 29-31 March, IberiCos 2010 - p. 6/13
Need for renormalization: variance of h(~x,t).
■
k
● Motivation and Summary
● Tensor Modes
● Amplitude of TM
In position space, the variance of the tensorial perturbations is defined as
R 3
R ∞ dk 2
2
2
~
hh i = d k|h~ (~x,t)| =
∆ (k)
■
● Need for renormalization
● Renormalization Method
● Tensor Perturbations
● Scalar Perturbations
● Time Dependence
● Conclusions
k
h
Due to the large k behavior of the modes the above integral is divergent:
i
R ∞ dk 16πGk3 h a
(2+3ε)
2
hh (~x,t)i = 0 k 4π2 a3 k [1 + 2k2 τ2 ] + ...
◆
● Testable Effects
0
◆
First term: quadratic divergence (typical in Minkowski).
Second term: logarithmic divergence (typical in expanding universe).
The End
■
Gonzalo J. Olmo
Little attention has been paid to these divergences:
◆ Sometimes this is bypassed by regarding h(~x,t) as a classical
random field and introducing a window function to remove the Fourier
modes with large k. But QFT is much more than Quantum Mechanics.
Porto, 29-31 March, IberiCos 2010 - p. 6/13
Need for renormalization: variance of h(~x,t).
■
k
● Motivation and Summary
● Tensor Modes
● Amplitude of TM
In position space, the variance of the tensorial perturbations is defined as
R 3
R ∞ dk 2
2
2
~
hh i = d k|h~ (~x,t)| =
∆ (k)
■
● Need for renormalization
● Renormalization Method
● Tensor Perturbations
● Scalar Perturbations
● Time Dependence
● Conclusions
k
h
Due to the large k behavior of the modes the above integral is divergent:
i
R ∞ dk 16πGk3 h a
(2+3ε)
2
hh (~x,t)i = 0 k 4π2 a3 k [1 + 2k2 τ2 ] + ...
◆
● Testable Effects
0
◆
First term: quadratic divergence (typical in Minkowski).
Second term: logarithmic divergence (typical in expanding universe).
The End
■
Little attention has been paid to these divergences:
◆ Sometimes this is bypassed by regarding h(~x,t) as a classical
random field and introducing a window function to remove the Fourier
modes with large k. But QFT is much more than Quantum Mechanics.
◆
It is also common to consider hh(x1 )h(x2 )i as the basic object.
R ∞ dk 2
sin k|~x−~x′ |
However, in FRW hh(x1 )h(x2 )i = 0 k ∆h (k) k|~x−~x′ | , so all the
nontrivial information is contained in hh2 i , which is ill defined.
Gonzalo J. Olmo
Porto, 29-31 March, IberiCos 2010 - p. 6/13
Renormalization in momentum space
■
● Motivation and Summary
We regard the variance hh2 i as the basic physical object, which defines
the amplitude of fluctuations in position space.
● Tensor Modes
● Amplitude of TM
● Need for renormalization
● Renormalization Method
● Tensor Perturbations
● Scalar Perturbations
● Time Dependence
● Testable Effects
● Conclusions
The End
Gonzalo J. Olmo
Porto, 29-31 March, IberiCos 2010 - p. 7/13
Renormalization in momentum space
■
We regard the variance hh2 i as the basic physical object, which defines
the amplitude of fluctuations in position space.
■
We treat h(~x,t) as a quantum entity
● Motivation and Summary
● Tensor Modes
● Amplitude of TM
● Need for renormalization
● Renormalization Method
● Tensor Perturbations
● Scalar Perturbations
● Time Dependence
⇒
RENORMALIZATION IN AN
EXPANDING UNIVERSE
● Testable Effects
● Conclusions
The End
Gonzalo J. Olmo
Porto, 29-31 March, IberiCos 2010 - p. 7/13
Renormalization in momentum space
■
We regard the variance hh2 i as the basic physical object, which defines
the amplitude of fluctuations in position space.
■
We treat h(~x,t) as a quantum entity
● Motivation and Summary
● Tensor Modes
● Amplitude of TM
● Need for renormalization
● Renormalization Method
⇒
● Tensor Perturbations
● Scalar Perturbations
● Time Dependence
RENORMALIZATION IN AN
EXPANDING UNIVERSE
● Testable Effects
● Conclusions
The End
Gonzalo J. Olmo
■
Since the physically relevant quantity (power spectrum) is expressed in
momentum space, the natural renormalization scheme to apply is the
so-called ADIABATIC SUBTRACTION (Parker-Fulling, ’74).
The DeWitt-Schwinger method gives the same results.
Porto, 29-31 March, IberiCos 2010 - p. 7/13
Renormalization in momentum space
■
We regard the variance hh2 i as the basic physical object, which defines
the amplitude of fluctuations in position space.
■
We treat h(~x,t) as a quantum entity
● Motivation and Summary
● Tensor Modes
● Amplitude of TM
● Need for renormalization
● Renormalization Method
⇒
● Tensor Perturbations
● Scalar Perturbations
● Time Dependence
RENORMALIZATION IN AN
EXPANDING UNIVERSE
● Testable Effects
● Conclusions
■
Since the physically relevant quantity (power spectrum) is expressed in
momentum space, the natural renormalization scheme to apply is the
so-called ADIABATIC SUBTRACTION (Parker-Fulling, ’74).
The DeWitt-Schwinger method gives the same results.
■
Adiabatic renormalization removes the divergences by subtracting (second
order) counterterms mode by mode in the integral
The End
n 2
h
oi
R
3
ä
1
1
ȧ
2 (k) − 16πGk
+
+
hh2 iren = 0∞ dk
∆
h
k
wk
a
4π2 a3
2w3k a2
Gonzalo J. Olmo
Porto, 29-31 March, IberiCos 2010 - p. 7/13
Renormalization of Tensorial Perturbations
■
● Motivation and Summary
● Tensor Modes
● Amplitude of TM
● Need for renormalization
Calculations give
hh2 iren
R ∞ dk 16πGk3 (−τπ) h (1)
|H (−kτ)|2 −
=
0
k
4π2 2a2
ν
i
(2+3ε)
2
1 + 2k2 τ2
π(−kτ)
● Renormalization Method
● Tensor Perturbations
● Scalar Perturbations
● Time Dependence
● Testable Effects
● Conclusions
The End
Gonzalo J. Olmo
Porto, 29-31 March, IberiCos 2010 - p. 8/13
Renormalization of Tensorial Perturbations
■
hh2 iren
● Motivation and Summary
● Tensor Modes
● Amplitude of TM
● Need for renormalization
● Renormalization Method
● Tensor Perturbations
● Scalar Perturbations
Calculations give
■
R ∞ dk 16πGk3 (−τπ) h (1)
|H (−kτ)|2 −
=
0
k
4π2 2a2
ν
i
(2+3ε)
2
1 + 2k2 τ2
π(−kτ)
Therefore, the renormalized expression for ∆2h (k) is
● Time Dependence
● Testable Effects
● Conclusions
The End
Gonzalo J. Olmo
∆˜ 2h (k) =
16πGk3 (−τπ)
4π2 2a2
h
i
(1)
(2+3ε)
2
1 + 2k2 τ2
|Hν (−kτ)|2 − π(−kτ)
Porto, 29-31 March, IberiCos 2010 - p. 8/13
Renormalization of Tensorial Perturbations
■
hh2 iren
● Motivation and Summary
● Tensor Modes
● Amplitude of TM
● Need for renormalization
● Renormalization Method
● Tensor Perturbations
Calculations give
■
● Scalar Perturbations
R ∞ dk 16πGk3 (−τπ) h (1)
|H (−kτ)|2 −
=
0
k
ν
4π2 2a2
i
(2+3ε)
2
1 + 2k2 τ2
π(−kτ)
Therefore, the renormalized expression for ∆2h (k) is
● Time Dependence
● Testable Effects
∆˜ 2h (k) =
● Conclusions
The End
■
16πGk3 (−τπ)
4π2 2a2
h
i
(1)
(2+3ε)
2
1 + 2k2 τ2
|Hν (−kτ)|2 − π(−kτ)
Evaluated at the Hubble radius crossing time we get
Pt (k)ren =
8α
MP2
where α ≈ 0.904 and ε ≡ −Ḣ/H 2 ≪ 1.
Gonzalo J. Olmo
H(tk ) 2
ε(tk )
2π
Porto, 29-31 March, IberiCos 2010 - p. 8/13
Renormalization of Tensorial Perturbations
■
hh2 iren
● Motivation and Summary
● Tensor Modes
● Amplitude of TM
● Need for renormalization
● Renormalization Method
● Tensor Perturbations
Calculations give
■
● Scalar Perturbations
R ∞ dk 16πGk3 (−τπ) h (1)
|H (−kτ)|2 −
=
0
k
ν
4π2 2a2
i
(2+3ε)
2
1 + 2k2 τ2
π(−kτ)
Therefore, the renormalized expression for ∆2h (k) is
● Time Dependence
● Testable Effects
∆˜ 2h (k) =
● Conclusions
The End
■
16πGk3 (−τπ)
4π2 2a2
h
i
(1)
(2+3ε)
2
1 + 2k2 τ2
|Hν (−kτ)|2 − π(−kτ)
Evaluated at the Hubble radius crossing time we get
Pt (k)ren =
8α
MP2
where α ≈ 0.904 and ε ≡ −Ḣ/H 2 ≪ 1.
■
H(tk ) 2
ε(tk )
2π
Recall that the unrenormalized value is
Pt (k) =
Gonzalo J. Olmo
8
MP2
H(tk ) 2
2π
Porto, 29-31 March, IberiCos 2010 - p. 8/13
Renormalization of Scalar Perturbations
■
Scalar perturbations are commonly studied through the gauge-invariant
quantity R (the comoving curvature perturbation) obeying
● Motivation and Summary
d2 R k
dτ2
● Tensor Modes
● Amplitude of TM
● Need for renormalization
● Renormalization Method
● Tensor Perturbations
● Scalar Perturbations
● Time Dependence
● Testable Effects
dz d R k
2
+ 2z dτ
dτ + k R k = 0
where z ≡ aφ̇0 /H, and with R k related to the inflaton field fluctuations via
R k = −Ψk − φ̇H δφk ..
0
● Conclusions
The End
Gonzalo J. Olmo
Porto, 29-31 March, IberiCos 2010 - p. 9/13
Renormalization of Scalar Perturbations
■
Scalar perturbations are commonly studied through the gauge-invariant
quantity R (the comoving curvature perturbation) obeying
● Motivation and Summary
d2 R k
dτ2
● Tensor Modes
● Amplitude of TM
● Need for renormalization
where z ≡ aφ̇0 /H, and with R k related to the inflaton field fluctuations via
● Renormalization Method
● Tensor Perturbations
R k = −Ψk − φ̇H δφk ..
● Scalar Perturbations
● Time Dependence
0
● Testable Effects
● Conclusions
The End
dz d R k
2
+ 2z dτ
dτ + k R k = 0
■
Proceeding as before (with care to treat the adiabatic counterterms for the
R k field) we get
hR
h
i
R
(1)
(2+3(3ε−η))
∞
dk
2
2i
2
3 −πτ
ren = 0 k 4πk 4(2π)3 z2 |Hµ (−τk)| − π(−kτ) 1 + 2(−kτ)2
where µ = 3/2 + 3ε − η and η = MP2 (V ′′ /V ).
Gonzalo J. Olmo
Porto, 29-31 March, IberiCos 2010 - p. 9/13
Renormalization of Scalar Perturbations
■
Scalar perturbations are commonly studied through the gauge-invariant
quantity R (the comoving curvature perturbation) obeying
● Motivation and Summary
d2 R k
dτ2
● Tensor Modes
● Amplitude of TM
● Need for renormalization
where z ≡ aφ̇0 /H, and with R k related to the inflaton field fluctuations via
● Renormalization Method
● Tensor Perturbations
R k = −Ψk − φ̇H δφk ..
● Scalar Perturbations
● Time Dependence
0
● Testable Effects
● Conclusions
dz d R k
2
+ 2z dτ
dτ + k R k = 0
■
The End
Proceeding as before (with care to treat the adiabatic counterterms for the
R k field) we get
hR
h
i
R
(1)
(2+3(3ε−η))
∞
dk
2
2i
2
3 −πτ
ren = 0 k 4πk 4(2π)3 z2 |Hµ (−τk)| − π(−kτ) 1 + 2(−kτ)2
where µ = 3/2 + 3ε − η and η = MP2 (V ′′ /V ).
■
The renormalized expression for ∆2R (k) is
∆˜ 2
R (k) =
Gonzalo J. Olmo
4πk3 (−πτ)
4(2π)3 z2
h
i
(1)
(2+3(3ε−η))
2
2
|Hµ (−τk)| − π(−kτ) 1 + 2(−kτ)2
Porto, 29-31 March, IberiCos 2010 - p. 9/13
Time Dependence
■
The renormalized amplitudes of the power spectra ∆˜ 2h (k) and ∆˜ 2R (k)
inherit the time-dependence of the counterterms.
● Motivation and Summary
● Tensor Modes
● Amplitude of TM
● Need for renormalization
● Renormalization Method
● Tensor Perturbations
● Scalar Perturbations
● Time Dependence
● Testable Effects
● Conclusions
The End
Gonzalo J. Olmo
Porto, 29-31 March, IberiCos 2010 - p. 10/13
Time Dependence
■
The renormalized amplitudes of the power spectra ∆˜ 2h (k) and ∆˜ 2R (k)
inherit the time-dependence of the counterterms.
● Motivation and Summary
● Tensor Modes
● Amplitude of TM
● Need for renormalization
● Renormalization Method
● Tensor Perturbations
● Scalar Perturbations
■
Since primordial fluctuations acquire classical properties soon after
crossing the Hubble radius, we find it natural to evaluate the renormalized
spectra at tk , or a few e-folds afterwards.
● Time Dependence
● Testable Effects
● Conclusions
The End
Gonzalo J. Olmo
Porto, 29-31 March, IberiCos 2010 - p. 10/13
Time Dependence
■
The renormalized amplitudes of the power spectra ∆˜ 2h (k) and ∆˜ 2R (k)
inherit the time-dependence of the counterterms.
● Motivation and Summary
● Tensor Modes
■
Since primordial fluctuations acquire classical properties soon after
crossing the Hubble radius, we find it natural to evaluate the renormalized
spectra at tk , or a few e-folds afterwards.
■
Assuming n > 1 but nε ≪ 1, we find that (n = number of e−folds)
2
H(t
)
2
k
˜ 2 (k, n) ≈ 2
◆ ∆
ε(tk )(2n − 3/2)
h
2π
MP
2
H(t
)
1
k
2
˜ (k, n) ≈ 2
◆ ∆
(3ε(tk ) − η(tk ))(2n − 3/2)
2π
R
2M ε(t )
● Amplitude of TM
● Need for renormalization
● Renormalization Method
● Tensor Perturbations
● Scalar Perturbations
● Time Dependence
● Testable Effects
● Conclusions
The End
P
k
The result is: r = 16ε(tk ) 3ε(t
Gonzalo J. Olmo
ε(tk )
k )−η(tk )
Porto, 29-31 March, IberiCos 2010 - p. 10/13
Time Dependence
■
The renormalized amplitudes of the power spectra ∆˜ 2h (k) and ∆˜ 2R (k)
inherit the time-dependence of the counterterms.
● Motivation and Summary
● Tensor Modes
■
Since primordial fluctuations acquire classical properties soon after
crossing the Hubble radius, we find it natural to evaluate the renormalized
spectra at tk , or a few e-folds afterwards.
■
Assuming n > 1 but nε ≪ 1, we find that (n = number of e−folds)
2
H(t
)
2
k
˜ 2 (k, n) ≈ 2
◆ ∆
ε(tk )(2n − 3/2)
h
2π
MP
2
H(t
)
1
k
2
˜ (k, n) ≈ 2
◆ ∆
(3ε(tk ) − η(tk ))(2n − 3/2)
2π
R
2M ε(t )
● Amplitude of TM
● Need for renormalization
● Renormalization Method
● Tensor Perturbations
● Scalar Perturbations
● Time Dependence
● Testable Effects
● Conclusions
The End
P
k
The result is: r = 16ε(tk ) 3ε(t
■
Gonzalo J. Olmo
ε(tk )
k )−η(tk )
The standard result r = 16ε(tk ) is recovered only if the counterterms are
evaluated at times well after the end of inflation (n > 100).
Porto, 29-31 March, IberiCos 2010 - p. 10/13
Time Dependence
■
The renormalized amplitudes of the power spectra ∆˜ 2h (k) and ∆˜ 2R (k)
inherit the time-dependence of the counterterms.
● Motivation and Summary
● Tensor Modes
■
Since primordial fluctuations acquire classical properties soon after
crossing the Hubble radius, we find it natural to evaluate the renormalized
spectra at tk , or a few e-folds afterwards.
■
Assuming n > 1 but nε ≪ 1, we find that (n = number of e−folds)
2
H(t
)
2
k
˜ 2 (k, n) ≈ 2
◆ ∆
ε(tk )(2n − 3/2)
h
2π
MP
2
H(t
)
1
k
2
˜ (k, n) ≈ 2
◆ ∆
(3ε(tk ) − η(tk ))(2n − 3/2)
2π
R
2M ε(t )
● Amplitude of TM
● Need for renormalization
● Renormalization Method
● Tensor Perturbations
● Scalar Perturbations
● Time Dependence
● Testable Effects
● Conclusions
The End
P
k
The result is: r = 16ε(tk ) 3ε(t
Gonzalo J. Olmo
ε(tk )
k )−η(tk )
■
The standard result r = 16ε(tk ) is recovered only if the counterterms are
evaluated at times well after the end of inflation (n > 100).
■
Though a better understanding of the decoherence processes is necessary
to fully determine the time scale at which the quantum-to-classical
transition really occurs, our predictions are accurate up to n ∼ 10 − 20).
Porto, 29-31 March, IberiCos 2010 - p. 10/13
Testable Effects
■
● Motivation and Summary
● Tensor Modes
● Amplitude of TM
● Need for renormalization
● Renormalization Method
Renormalization also affects the spectral indices:
Standard Values
◆ nt = −2ε
◆
● Tensor Perturbations
● Scalar Perturbations
● Time Dependence
● Testable Effects
● Conclusions
◆
ns − 1 = 2(η − 3ε)
nt′ = −nt (1 − ns + nt )
Renormalized Values
◆ nt = 2(ε − η)
(12ε2 −8εη+ξ)
3ε−η
◆
ns − 1 = 2(η − 3ε) +
◆
nt′ = 8ε(ε − η) + 2ξ , where ξ ≡ MP4 (V ′V ′′′ /V 2 ).
The End
Gonzalo J. Olmo
Porto, 29-31 March, IberiCos 2010 - p. 11/13
Testable Effects
■
Renormalization also affects the spectral indices:
● Tensor Modes
● Amplitude of TM
● Need for renormalization
◆
● Renormalization Method
● Tensor Perturbations
● Scalar Perturbations
◆
● Time Dependence
● Testable Effects
● Conclusions
Renormalized Values
◆ nt = 2(ε − η)
Standard Values
◆ nt = −2ε
● Motivation and Summary
■
ns − 1 = 2(η − 3ε)
nt′ = −nt (1 − ns + nt )
(12ε2 −8εη+ξ)
3ε−η
◆
ns − 1 = 2(η − 3ε) +
◆
nt′ = 8ε(ε − η) + 2ξ , where ξ ≡ MP4 (V ′V ′′′ /V 2 ).
We find a new consistency relation for single field inflation
The End
r = 4(1 − ns − nt ) +
Gonzalo J. Olmo
4nt′
nt2 −2nt′
1 − ns −
q
2nt′ + (1 − ns )2 − nt2
Porto, 29-31 March, IberiCos 2010 - p. 11/13
Testable Effects
■
Renormalization also affects the spectral indices:
● Tensor Modes
● Amplitude of TM
● Need for renormalization
◆
● Renormalization Method
● Tensor Perturbations
● Scalar Perturbations
◆
● Time Dependence
● Testable Effects
● Conclusions
Renormalized Values
◆ nt = 2(ε − η)
Standard Values
◆ nt = −2ε
● Motivation and Summary
■
ns − 1 = 2(η − 3ε)
nt′ = −nt (1 − ns + nt )
(12ε2 −8εη+ξ)
3ε−η
◆
ns − 1 = 2(η − 3ε) +
◆
nt′ = 8ε(ε − η) + 2ξ , where ξ ≡ MP4 (V ′V ′′′ /V 2 ).
We find a new consistency relation for single field inflation
The End
r = 4(1 − ns − nt ) +
■
4nt′
nt2 −2nt′
1 − ns −
q
2nt′ + (1 − ns )2 − nt2
The standard prediction r = −8nt requires nt < 0 .
Our prediction also allows for nt ≥ 0 .
Gonzalo J. Olmo
Porto, 29-31 March, IberiCos 2010 - p. 11/13
Testable Effects
■
Renormalization also affects the spectral indices:
● Tensor Modes
● Amplitude of TM
● Need for renormalization
◆
● Renormalization Method
● Tensor Perturbations
● Scalar Perturbations
◆
● Time Dependence
● Testable Effects
● Conclusions
Renormalized Values
◆ nt = 2(ε − η)
Standard Values
◆ nt = −2ε
● Motivation and Summary
■
ns − 1 = 2(η − 3ε)
nt′ = −nt (1 − ns + nt )
(12ε2 −8εη+ξ)
3ε−η
◆
ns − 1 = 2(η − 3ε) +
◆
nt′ = 8ε(ε − η) + 2ξ , where ξ ≡ MP4 (V ′V ′′′ /V 2 ).
We find a new consistency relation for single field inflation
The End
r = 4(1 − ns − nt ) +
■
4nt′
nt2 −2nt′
1 − ns −
q
2nt′ + (1 − ns )2 − nt2
The standard prediction r = −8nt requires nt < 0 .
Our prediction also allows for nt ≥ 0 .
■
The standard prediction constrains nt′ = −nt (1 − ns + nt ) .
In our case nt′ is a new observable !!!
Gonzalo J. Olmo
Porto, 29-31 March, IberiCos 2010 - p. 11/13
Testable Effects
■
Renormalization also affects the spectral indices:
● Tensor Modes
● Amplitude of TM
● Need for renormalization
◆
● Renormalization Method
● Tensor Perturbations
● Scalar Perturbations
◆
● Time Dependence
● Testable Effects
● Conclusions
Renormalized Values
◆ nt = 2(ε − η)
Standard Values
◆ nt = −2ε
● Motivation and Summary
■
ns − 1 = 2(η − 3ε)
nt′ = −nt (1 − ns + nt )
(12ε2 −8εη+ξ)
3ε−η
◆
ns − 1 = 2(η − 3ε) +
◆
nt′ = 8ε(ε − η) + 2ξ , where ξ ≡ MP4 (V ′V ′′′ /V 2 ).
We find a new consistency relation for single field inflation
The End
r = 4(1 − ns − nt ) +
■
4nt′
nt2 −2nt′
1 − ns −
q
2nt′ + (1 − ns )2 − nt2
The standard prediction r = −8nt requires nt < 0 .
Our prediction also allows for nt ≥ 0 .
■
The standard prediction constrains nt′ = −nt (1 − ns + nt ) .
In our case nt′ is a new observable !!!
■
Gonzalo J. Olmo
For more details and references see Phys.Rev. D81,043514(2010).
Porto, 29-31 March, IberiCos 2010 - p. 11/13
Conclusions
■
● Motivation and Summary
● Tensor Modes
The predictions of (single-field) slow-roll inflation change significantly if
renormalization in curved spacetimes is taken into account and the
counterterms are evaluated around the time of Hubble horizon exit.
● Amplitude of TM
● Need for renormalization
● Renormalization Method
● Tensor Perturbations
● Scalar Perturbations
● Time Dependence
● Testable Effects
● Conclusions
The End
Gonzalo J. Olmo
Porto, 29-31 March, IberiCos 2010 - p. 12/13
Conclusions
■
The predictions of (single-field) slow-roll inflation change significantly if
renormalization in curved spacetimes is taken into account and the
counterterms are evaluated around the time of Hubble horizon exit.
■
Renormalization provides a new consistency condition that relates the
tensor-to-scalar amplitude ratio with the spectral indices.
● Motivation and Summary
● Tensor Modes
● Amplitude of TM
● Need for renormalization
● Renormalization Method
● Tensor Perturbations
● Scalar Perturbations
● Time Dependence
● Testable Effects
● Conclusions
The End
ε
r = 16ε 3ε−η
nt = 2(ε − η)
ns − 1 = 2(η − 3ε) +
(12ε2 −8εη+ξ)
3ε−η
nt′ = 8ε(ε − η) + 2ξ
Gonzalo J. Olmo
Porto, 29-31 March, IberiCos 2010 - p. 12/13
Conclusions
■
The predictions of (single-field) slow-roll inflation change significantly if
renormalization in curved spacetimes is taken into account and the
counterterms are evaluated around the time of Hubble horizon exit.
■
Renormalization provides a new consistency condition that relates the
tensor-to-scalar amplitude ratio with the spectral indices.
● Motivation and Summary
● Tensor Modes
● Amplitude of TM
● Need for renormalization
● Renormalization Method
● Tensor Perturbations
● Scalar Perturbations
● Time Dependence
● Testable Effects
● Conclusions
ε
r = 16ε 3ε−η
The End
nt = 2(ε − η)
ns − 1 = 2(η − 3ε) +
(12ε2 −8εη+ξ)
3ε−η
nt′ = 8ε(ε − η) + 2ξ
■
Gonzalo J. Olmo
Only when the counterterms are evaluated at times well beyond the end of
inflation does one recover the standard predictions. A deeper
understanding of the quantum-to-classical transition is necessary.
Porto, 29-31 March, IberiCos 2010 - p. 12/13
Conclusions
■
The predictions of (single-field) slow-roll inflation change significantly if
renormalization in curved spacetimes is taken into account and the
counterterms are evaluated around the time of Hubble horizon exit.
■
Renormalization provides a new consistency condition that relates the
tensor-to-scalar amplitude ratio with the spectral indices.
● Motivation and Summary
● Tensor Modes
● Amplitude of TM
● Need for renormalization
● Renormalization Method
● Tensor Perturbations
● Scalar Perturbations
● Time Dependence
● Testable Effects
● Conclusions
ε
r = 16ε 3ε−η
The End
nt = 2(ε − η)
ns − 1 = 2(η − 3ε) +
(12ε2 −8εη+ξ)
3ε−η
nt′ = 8ε(ε − η) + 2ξ
Gonzalo J. Olmo
■
Only when the counterterms are evaluated at times well beyond the end of
inflation does one recover the standard predictions. A deeper
understanding of the quantum-to-classical transition is necessary.
■
The new generation of high precision detectors may soon turn QFT in
curved spacetimes into an experimental science. Our results indicate that
renormalization may play an important role in the interpretation of the
observational data.
Porto, 29-31 March, IberiCos 2010 - p. 12/13
● Motivation and Summary
● Tensor Modes
● Amplitude of TM
● Need for renormalization
● Renormalization Method
● Tensor Perturbations
● Scalar Perturbations
● Time Dependence
● Testable Effects
● Conclusions
Thanks !!!
The End
Gonzalo J. Olmo
Porto, 29-31 March, IberiCos 2010 - p. 13/13