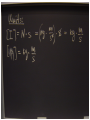Download Spring 2016 - PHYS1211 Impulse, Linear Momentum, and the Law of

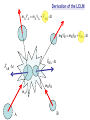
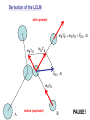
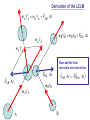
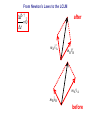
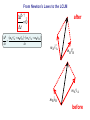
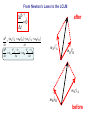
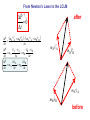
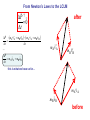
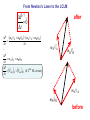
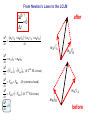
Spring 2016 - PHYS1211
Impulse, Linear Momentum, and the Law of
Conservation of Linear Momentum
(Dr. Andrei Galiautdinov, UGA)
Introducing momentum
A quantity that characterizes the
moving object. It captures both
aspects of object’s motion:

mv
This guy may have a few things to say
about momentum…
Dynamical
aspect: how
difficult it is to
change object’s
velocity
Kinematical
aspect: how fast
and in which
direction the
object is moving
Momentum has its own conservation law!
A bit of history…
Galileo (1564-1642)
1600
Newton (1643-1727)
17th Century
1687
1700
The impulse-momentum theorem
It all boils down to re-writing Newton’s 2nd Law in the form
which explicitly takes into account the finite duration of
the action of the net force.
The Impulse-Momentum Theorem
It all boils down to re-writing Newton’s 2nd Law in the form that explicitly takes into account the finite duration of the
action of the net force.
Calculus-based approach:
5
6
It might be easier to think about impulse
delivered by a variable force in terms of the
same impulse delivered by some constant
average force. This is how it is done in algebrabased class.
7
The Impulse-Momentum Theorem
It all boils down to re-writing Newton’s 2nd Law in the form that explicitly takes into account the finite duration of the
action of the net force.
Algebra-based approach:
8
9
The Impulse-Momentum Theorem
So we have:
But I like to write it differently:



I = mv f - mvi

 
mv f = mvi + I
The I.M.T. tells us how momentum of a particular object participating in the
interaction changes. Let’s look at it more closely…


pi = mvi
The Impulse-Momentum Theorem
We have:
But I like to write it differently:



I = mv f - mvi

 
mv f = mvi + I

I


pi = mvi
The Impulse-Momentum Theorem
We have:
But I like to write it differently:



I = mv f - mvi

 
mv f = mvi + I


pf = mv f


pi = mvi

I
Forces come from interactions
IMPORTANT:
Forces come from interactions, which means that…
…in any impulse delivery, apart from the object “receiving” the impulse, there is
always another object, the agent, which “delivers” that impulse (and vice versa!)
Interaction involving a single object is like one-hand clapping.
IT NEVER HAPPENS!
The LCLM
Derivation of the LCLM



mA v′A = mA v A + FAB ⋅ ∆t



mB v′B = mB v B + FBA ⋅ ∆t

FBA ⋅ ∆t

FAB ⋅ ∆t

mA v A
A

mB v B
B

mA v′A
after (primed)

mB v′B
The LCLM

mA v′A

mA v A
A

mB v′B

mB v B
before (unprimed)
B

mB v B

mA v A
Derivation of the LCLM
Derivation of the LCLM
after (primed)



mB v′B = mB v B + FBA ⋅ ∆t

mB v B

mB v′B

FBA ⋅ ∆t

mB v B
A
before (unprimed)
B
PAUSE!
Derivation of the LCLM



mA v′A = mA v A + FAB ⋅ ∆t

mA v′A

mA v A

FAB ⋅ ∆t

mA v A
A
B
Derivation of the LCLM



mA v′A = mA v A + FAB ⋅ ∆t

mA v′A

FAB ⋅ ∆t

mA v A
A



mB v′B = mB v B + FBA ⋅ ∆t

mA v A
Now add the final
momenta and notice that

FBA ⋅ ∆t

mB v B
(


FAB ⋅ ∆t = − FBA ⋅ ∆t
B
)

mA v′A
Once again, to recapitulate:
after (primed)

mB v′B

mA v′A

mA v A
A

mB v′B

mB v B
before (unprimed)
B

mB v B

mA v A
For the LCLM to hold, the system must be closed!
That means that:
1.
The colliding objects interact solely with each other and are not acted upon by
anything external. (Or, if the interaction with the outside world is happening, all
external forces must add up to zero.)
2.
No material is added to or taken away from the system during the experiment.
Intuitively we feel it should be like that!
On the other hand, here are some very fun things that could (and most likely will) ruin
your chances at seeing the LCLM in action:
•Pushing or pulling on either body during the collision.
•Doing your collision experiment on a table covered with honey.
•Pouring cement on top of the objects (say, carts on the air track) while they
undergo a collision.
•.............................. (Millions of others. Invent your own!)
23
Some old slides in case you find them useful…
24
Completely inelastic collisions
(objects get stuck together)
25
26
1D Magnetic recoil demonstrated…
… and, hopefully, everything went well...
RECOIL IN ACTION:
Recoil
(Case 1: both objects are initially at rest)
28
29
After:
30
After:
31
Recoil
(Case 2: both objects are initially moving
together)
32
A recoil example. A person jumps off the back of the moving cart.
33
Another recoil example. This time a person jumps forward:
Same concept, different context: pilot ejects from a vertically moving spacecraft:
34
I forgot to take the pic with numbers inserted. Do on your own.
35
Completely elastic collisions
(a special kind of collisions in which total kinetic
energy is conserved!)
36
The goal is to derive the formulas on the bottom of page.
37
Completely elastic collisions
(Case 1: cart B is initially at rest)
Only this case is needed for the test.
38
39
Completely elastic collisions
(Case 2: both A & B are moving)
Not needed for test.
40
41
Extra slides
A note on masses
Mass is a measure of the inertial property of a
given object (how “difficult” it is to change
that object’s velocity).
Possible operational definition of mass:
We define the ratio of two masses by the
inverse ratio of the accelerations
experienced by the “masses” when they
are subjected to equal forces:
mA  aA 

≡ 
mB  aB 
−1
So we don’t even need the force scale. All we
need is the criterion for “equality” of two
forces (say, “spring stretched by same
amount,” etc.)
a
aA
aB
FA = FB
mA  aA 

≡ 
mB  aB 
−1
F
2
= 
1
−1
=
1
2
From Newton’s Laws to the LCLM

∆P ? 
=0
∆t
after

mA v′A

mB v B

mB v′B

mA v A
before
From Newton’s Laws to the LCLM

∆P ? 
=0
∆t





∆P (mA v′A + mB v′B ) − (mA v A + mB v B )
=
∆t
∆t
after

mA v′A

mB v B

mB v′B

mA v A
before
From Newton’s Laws to the LCLM

∆P ? 
=0
∆t





∆P (mA v′A + mB v′B ) − (mA v A + mB v B )
=
∆t
∆t





v′A − v A
v′B − v B
∆P
= mA
+ mB
∆t
∆t
∆t
after

mA v′A

mB v B

mB v′B

mA v A
before
From Newton’s Laws to the LCLM

∆P ? 
=0
∆t





∆P (mA v′A + mB v′B ) − (mA v A + mB v B )
=
∆t
∆t





v′A − v A
v′B − v B
∆P
= mA
+ mB
∆t
∆t
∆t



∆v B
∆P
∆v A
= mA
+ mB
∆t
∆t
∆t
after

mA v′A

mB v B

mB v′B

mA v A
before
From Newton’s Laws to the LCLM

∆P ? 
=0
∆t

∆P
∆t

∆P
∆t

∆P
∆t

∆P
∆t




(
mA v′A + mB v′B ) − (mA v A + mB v B )
=
∆t




v′A − v A
v′B − v B
= mA
+ mB
∆t
∆t


∆v A
∆v B
= mA
+ mB
∆t
∆t


= mA aA + mB aB
after

mA v′A

mB v B

mB v′B

mA v A
before
From Newton’s Laws to the LCLM

∆P ? 
=0
∆t





∆P (mA v′A + mB v′B ) − (mA v A + mB v B )
=
∆t
∆t
...



∆P
= mA aA + mB aB
∆t
after

mA v′A

mB v′B
this is what we have so far…

mB v B

mA v A
before
From Newton’s Laws to the LCLM

∆P ? 
=0
∆t





∆P (mA v′A + mB v′B ) − (mA v A + mB v B )
=
∆t
∆t
...



∆P
= mA aA + mB aB
∆t



∆P
= Fnet A + Fnet B (if 2 nd NL is true)
∆t
after

mA v′A

mB v′B
( ) ( )

mB v B

mA v A
before
From Newton’s Laws to the LCLM

∆P ? 
=0
∆t

∆P
∆t
...

∆P
∆t

∆P
∆t

∆P
∆t




(
mA v′A + mB v′B ) − (mA v A + mB v B )
=
∆t
after

mA v′A


= mA aA + mB aB
( ) ( )B

= Fnet

A + Fnet


= FAB + FBA

mB v′B
(if 2 nd NL is true)
(if system is closed)

mB v B

mA v A
before
From Newton’s Laws to the LCLM

∆P ? 
=0
∆t

∆P
∆t
...

∆P
∆t

∆P
∆t

∆P
∆t

∆P
∆t




(
mA v′A + mB v′B ) − (mA v A + mB v B )
=
∆t
after

mA v′A


= mA aA + mB aB
( ) ( )B

= Fnet

A + Fnet


= FAB + FBA
(

mB v′B
(if 2 nd NL is true)
(if system is closed)
)


= FAB + − FAB (if 3rd NL is true)

mB v B

mA v A
before
From Newton’s Laws to the LCLM

∆P ? 
=0
∆t

∆P
∆t
...

∆P
∆t

∆P
∆t

∆P
∆t

∆P
∆t

∆P
∆t




(
mA v′A + mB v′B ) − (mA v A + mB v B )
=
∆t
after

mA v′A


= mA aA + mB aB
( ) ( )B

= Fnet

A + Fnet


= FAB + FBA
(
(if 2 nd NL is true)
(if system is closed)
)


= FAB + − FAB (if 3rd NL is true)

=0

mB v′B

mB v B

mA v A
before
From Newton’s Laws to the LCLM

∆P ? 
=0
∆t





∆P (mA v′A + mB v′B ) − (mA v A + mB v B )
=
∆t
∆t





v′A − v A
v′B − v B
∆P
+ mB
= mA
∆t
∆t
∆t



∆v
∆v
∆P
= mA A + mB B
∆t
∆t
∆t



∆P
= mA aA + mB aB
∆t



∆P
= Fnet A + Fnet B (if 2 nd NL is true)
∆t


∆P 
= FAB + FBA (if system is closed)
∆t


∆P 
= FAB + − FAB (if 3rd NL is true)
∆t

∆P 
=0
∆t
after

mA v′A

mB v′B
( ) ( )
(
)

mB v B

mA v A
before
The End
55