Download The Fundamental Theorem of Calculus

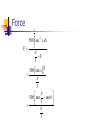
The Fundamental Theorem of
Calculus
Inverse Operations
Fundamental Theorem of
Calculus


Discovered independently by Gottfried
Liebnitz and Isaac Newton
Informally states that differentiation
and definite integration are inverse
operations.
Fundamental Theorem of
Calculus

If a function f is continuous on the
closed interval [a, b] and F is an
antiderivative of f on the interval [a,
b], then

b
a
f ( x) dx  F (b)  F (a)
Guidelines for Using the
Fundamental Theorem of Calculus
1.
2.
Provided you can find an antiderivative
of f, you now have a way to evaluate a
definite integral without having to use
the limit of a sum.
When applying the Fundamental
Theorem of Calculus, the following
notation is used
Guidelines

b
a
f ( x)dx  F ( x)]  F (b)  F (a)
b
a
It is not necessary to include a constant of
integration C in the antiderivative because
they cancel out when you subtract.
Evaluating a Definite Integral
Evaluate each definite integral.

7
2
7
3dv  3 dv  3v]72  21  6  15
1
2
1
2 (u  u 2 )du
u2
1 1
u

u
dx


u
]2


2
2
  1 2 1    2  2 1 

 
 
 2
1   2
2 

 1 3
        2
 2 2
1
2
Evaluate the Definite Integral

2

1

sin

4
0  cos2  


4
0
 cos 

2
cos


2

] 
4
0

4


4
d


1 d


0

0 

4
Evaluate the Definite Integral


4
0
2
sec x dx

 tan x 0  tan
4

4
 tan 0  1  0  1
Definite Integral Involving
Absolute Value


2
0
Evaluate
2 x  1 dx
The absolute value function has to be broken up
into its two parts:

2 x  1
2x  1  
2 x  1

1
if x 
2
1
if x 
2
Definite Integral Involving
Absolute Value
Now evaluate each part separately
1
2
0
  2x  1 dx  
2
1
2
1
2
0
(2 x  1) dx
2
  x  x   x  x  1
2
2
2
2
  1 2  1  
 2
 1   1 
          0   2  2        
 2   2  
  2   2  

1
1 5
 2 
4
4 2
Using the Fundamental
Theorem to Find Area


Find the area of the region bounded by
the graph of y = 2x3 – 3x + 2, the xaxis, and the vertical lines x = 0 and
x=2
Using the Fundamental
Theorem to Find Area
Area
   2 x  3 x  2  dx
2
3
0
2
 2 x 3x



 2x
2
 4
0
 8  6  4    0  0  0 
4
6
2
The Mean Value Theorem for
Integrals

If f is continuous on the closed interval
[a, b], then there exists a number c in the
closed interval [a, b] such that

b
a
f ( x) dx  f (c)(b  a).
Average Value of a Function



This is just another way to write the
Mean Value Theorem (mean = average
in mathematics)
If f is integrable on the closed interval
[a,b], then the average value of f on
the interval is
Average Value of a Function

c
b
a
f ( x) dx
ba
Finding the Average Value of a
Function


Find the average value of
f(x) = sin x on the interval [0, ]

c

0

sin x dx
 0
1  1



2

cos x 0


Force


The force F (in newtons) of a hydraulic
cylinder in a press is proportional to the
square of sec x, where x is the distance
(in meters) that the cylinder is extended
in its cycle. The domain of F is
[0, /3] and F(0) = 500.
Force

(a) Find F as a function of x.
F(x) = 500 sec2 x
(b) Find the average force exerted by the
press over the interval [0, /3]
Force

3
F
500  sec 2 x dx
0

3
0


500  tan x 0 3

3
 

500  tan  tan 0 
3




3
Force


500

3 0

3
500 3

3


1500 3

 827 Newtons
Second Fundamental Theorem
of Calculus

If f is continuous on an open interval
I containing a, then, for every x in
the interval,
d  x

f
(
t
)
dt

f
(
x
)




dx a
Using the Second Fundamental
Theorem of Calculus

Evaluate
x
d 
2
F ( x)   t (t  1) dt 

0
dx 
 x( x 2  1)  x3  x
Second Fundamental Theorem
of Calculus

Find F’(x) of
F ( x)  
x2
2
1
dt
3
t
1
2
 6  2x   5
x
x