* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download lecture
Internal energy wikipedia , lookup
Renormalization group wikipedia , lookup
Density of states wikipedia , lookup
Relativistic quantum mechanics wikipedia , lookup
Eigenstate thermalization hypothesis wikipedia , lookup
Aharonov–Bohm effect wikipedia , lookup
Nuclear structure wikipedia , lookup
Theoretical and experimental justification for the Schrödinger equation wikipedia , lookup
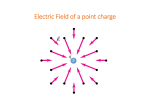
§2.4 Electric work and energy Christopher Crawford PHY 311 2014-02-12 Outline • Electric work and energy Energy of a charge distribution Energy density in terms of E field • Field lines and equipotentials Drawing field lines Flux x flow analogy • Poisson’s equation Curvature of function Green’s functions Helmholtz theorem 2 Energy of a charge distribution • Reminder of meaning: potential x charge = potential energy • Integrating energy over a continuous distribution • Continuous version 3 Energy of the electric field • Integration by parts – Derivative chain • Philosophical questions: – is the energy stored in the field, or in the force between the charges? – is the electric field real, or just a calculational device? potential field? – if a tree falls in the forest ... 4 Superposition • Force, electric field, electric potential all superimpose • Energy is quadratic in fields, not linear – – – – the cross term is the `interaction energy’ between two distributions the work required to bring two systems of charge together W1 and W2 are infinite for point charges – self-energy E1E2 is negative for a dipole (+q, -q) 5 Velocity field: flux, flow, [and fish] 6 Electric flux and flow FLUX FLOW • Field lines (flux tubes) • Equipotential (flow) surfaces counts potential diffs. ΔV from a to b E = flow density ~ energy/charge counts charges inside surface D = ε0E = flux density ~ charge Closed surfaces because E is conservative FLUX x FLOW • Energy density (boxes) counts energy in any volume D E ~ charge x energy/charge B.C.’s: Flux lines bounded by charge Flow sheets continuous (equipotentials) 7 Plotting field lines and equipotentials 8 Green’s function G(r,r’) • The potential of a point-charge • A simple solution to the Poisson’s equation • Zero curvature except infinite at one spot 9 General solution to Poisson’s equation • Expand f(x) as linear combination of delta functions • Invert linear Lapacian on each delta function individually 10 Green’s functions as propagators • Action at a distance: G(r’,r) `carries’ potential from source at r' to field point (force) at r • In quantum field theory, potential is quantized G(r’,r) represents the photon (particle) that carries the force • How to measure `shape’ of the proton? 11 Putting it all together… • Solution of Maxwell’s equations 12