* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Document
Hall effect wikipedia , lookup
History of electrochemistry wikipedia , lookup
Magnetohydrodynamics wikipedia , lookup
Electrostatic generator wikipedia , lookup
Electroactive polymers wikipedia , lookup
Maxwell's equations wikipedia , lookup
Electron mobility wikipedia , lookup
Electrodynamic tether wikipedia , lookup
Faraday paradox wikipedia , lookup
Lorentz force wikipedia , lookup
Nanofluidic circuitry wikipedia , lookup
Electromotive force wikipedia , lookup
Electric current wikipedia , lookup
Electricity wikipedia , lookup
Static electricity wikipedia , lookup
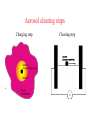
Aerosol protection of laser optics by Electrostatic Fields (not manetic) L. Bromberg ARIES Meeting Madison WI April 23, 2002 Motivation • Aerosols are created in chamber due to large heating flux on surface of liquid, nucleation in the volume, …. • Aerosols are charged, due to presence of plasma afterglow following the pulse • Electric fields can be used to remove aerosol • Similar to electrostatic precipitators used commercially for removing particulate matter from industrial flows Structure of talk • Charge state of aerosols exposed to plasma conditions • Motion of charged aerosols under the presence of an electric field • Implications to IFE laser optics Aerosol clearing steps Charging step Clearing step Aerosol charging • In the presence of a plasma, a particulate charge varies as dq/dt = Ii+Ie where Ie = - p a2 e ve ne exp ( -e2 | Z | / e0 a Te) Ii = p a2 e vi ni (1 + e2 | Z | / e0 a Ti) • Z is the average number of electronic charges in the particulate • It is assumed that all radiation fields have decayed away • Good for times > 1 microsecond • In the presence of irradiation: • If Jph > e p a2 Y-1 ve ne , different sign sheath Ie = - p a2 e ve ne (1 + e2 | Z | / e0 a Te) Ii = p a2 e vi ni exp ( -e2 | Z | / e0 a Te) Iph = jph e Y exp( -e2 | Z | / a Tph) • • Much faster equilibration times, due to the lack of ion contribution to the charging But at the large intensities, aerosols will not survive… Average electronic charge number vs Te for several densities 35000 Number of electronic charges on aerosol 30000 ne = 5 1018 - 2 1019 m-3 ne : 5.e18 - 2.e19 /m3 25000 a = 10 mm 20000 15000 10000 5000 0 0 2 4 6 8 T e (eV) 10 12 14 16 Average electronic charge number vs aerosol size 9000 8000 Te = 5 eV 7000 Elementary charge number Ti = 0.2 eV 6000 5000 4000 For electrostratic precipitators (Q ~ d2) 3000 0.1 mm 3 1 mm 165 10 mm 16500 2000 1000 0 0.0E+00 2.0E-06 4.0E-06 6.0E-06 Aerosol diameter (m) 8.0E-06 1.0E-05 1.2E-05 Time evolution of aerosol charging • Aerosol charge equilibrates very fast with background • ~ several microseconds at densities of 1015 /m3 • Aerosol charge not very dependent on initial state • Initial aerosol charge depends on radiation field and fast electron/ion bombardment • Aerosols are charged at higher rates than in ESP Impact of presence or absence of plasma in front of the mirrors • If there is a plasma present in the space in front of the final optics mirrors • Aerosols are charged negatively and move to the location of highest potential • In etching reactors (for the semiconductor industry), accumulation of aerosols somewhere in between electrodes • As long as there is a plasma and limited velocity of the gas, aerosols do not deposit on the surface • If vgas > 0.1 m/s, deposition could occur • Deposition occurs by impaction (separation from flow due to acceleration from changing flow direction), and by diffusion • If there is no plasma, it is possible to establish an electric field to remove the charged aerosols. SPATIAL AEROSOL DISTRIBUTION IN THE PRESENCE OF PLASMA Aerosol motion in the presence of an electric field Absence of plasma • The motion of a particulate in a gas under the effect of an applied field is given by: v = Zp E E is the applied electric field and Zp is the particulate mobility: Zp = qp Cc / 3 p a where qp is the particulate charge Cc is the Cunningham correction factor is the gas viscosity a is the particulate radius Cc = 1 + Kn ( 1.25 + 0.40 exp( -1.1/ Kn ) ) Kn = 2 l / a, l being the mean free path of the a gas molecule For Xe at 1 Torr (STP), l = 2.62 x 10-5 m Gas viscosity • For Xenon, • m ~ 44 mPa s at 600K At 1000 K, m ~ 70 mPa s viscosity (micro Pa s) • Using the kinetic theory of transport gases (assuming hard sphere collisions): 90 • = ( T / T0 ) 1/2 80 (independent of density!!!) 70 60 50 40 y = 0.3282x 0. 7649 30 20 10 0 0 500 Te m per atur e (K) 1000 1500 Aerosol velocity 10 kV/m, 1 Torr Xe, 5 eV 0.16 0.14 aerosol velocity (m/s) 0.12 0.10 0.08 0.06 0.04 0.02 0.00 1.0E-07 1.0E-06 1.0E-05 Aerosol diameter (m) 1.0E-04 Electrostatic removal of aerosols evaluation for laser optics ESP 760 0.06 pressure (STP) Electron temperature Viscosity, Xe Mean Free path Torr eV Pa s m 1 5 7.0E-05 2.6E-05 Aerosol diameter Knudsen number Cunningham factor m 1.0E-06 52.4 87 1.0E-06 320 6.8E-06 10000 165 1.8E-07 100000 0.068 0.09 Elementary charges Mobility Applied electric field m2/V s V/m Aerosol velocity m/s Aerosol clearing with electric fields • Velocity of aerosols is sufficient for removal of aerosols in front of mirrors • ~ several cm/s • Limited speed of flow in front of mirrors to prevent deposition of aerosols by impaction (depositon due to change of velocity of the fluid) • Relatively large electric fields are required (100 V/cm) • Capacitive field generation requires electrodes in chamber • Mirror themselves could serve as an electrode • Second electrode a short disctance (10 cm) away from mirrors