Download Electrical properties

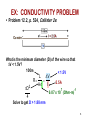
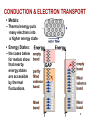
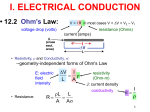
CHAPTER 12:
ELECTRICAL PROPERTIES
ISSUES TO ADDRESS...
• How are electrical conductance and resistance
characterized?
• What are the physical phenomena that distinguish
conductors, semiconductors, and insulators?
• For metals, how is conductivity affected by
imperfections, T, and deformation?
• For semiconductors, how is conductivity affected
by impurities (doping) and T?
1
Chapter 12 – Electrical Properties
• Motivation
– Why would you care about understanding how materials respond
to applied electric fields?
VIEW OF AN INTEGRATED CIRCUIT
• Scanning electron microscope images of an IC:
Al
Si
(doped)
(d)
(a)
45m
0.5mm
• A dot map showing location of Si (a semiconductor):
--Si shows up as light regions.
(b)
• A dot map showing location of Al (a conductor):
--Al shows up as light regions.
Fig. (d) from Fig. 18.25, Callister 6e. (Fig. 18.25 is
courtesy Nick Gonzales, National Semiconductor
Corp., West Jordan, UT.)
(c)
Fig. (a), (b), (c) from Fig. 18.0,
Callister 6e.
2
Chapter 12 – Electrical Properties
• Introduction – Electrical conduction
– The next several slides you have seen before (Physics)
– Ohm’s law – relation between current I (time rate of charge
passage) and the applied voltage
V  IR
V []Volts( J / C ) I [] Amperes(C / s) R[]ohms(V / A)
• R – resistance, influenced by specimen configuration,
often independent of current
• Resistivity r
r
RA
l
r
VA
, r[]  m
lI
A – cross sectional area perpendicular to current
l – distance between points where V is measured
Chapter 12 – Electrical Properties
• Introduction – Electrical conductivity
– Typically the electrical conductivity is used to specify the
electrical properties of materials

1
r
,  []  m 
1
• Conductivity describes the ease with which a material is
capable of conducting an electrical current
• Can also express Ohm’s law as
ξ is field intensity, J is the current density,
J = σξ; ξ = V/ l
and l is the distance between points
where V is applied
Amazing point – solids exhibit a range of electrical conductivities
spanning over 27 orders of magnitude!
ELECTRICAL CONDUCTION
• Ohm's Law:
DV = I R
voltage drop (volts)
current (amps)
resistance (Ohms)
• Resistivity, r and Conductivity, :
--geometry-independent forms of Ohm's Law
E: electric
field
intensity
• Resistance: R 
DV I
 r
L
A
rL
L

A A
resistivity
(Ohm-m)
J: current density
conductivity
I

r
3
CONDUCTIVITY: COMPARISON
• Room T values (Ohm-m)
-1
Selected values from Tables 18.1, 18.2, and 18.3, Callister 6e.
4
EX: CONDUCTIVITY PROBLEM
• Problem 12.2, p. 524, Callister 2e:
What is the minimum diameter (D) of the wire so that
DV < 1.5V?
100m
< 1.5V
L
DV
R

2.5A
A
I
D2
7
-1
6.07 x 10 (Ohm-m)
4
Solve to get D > 1.88 mm
5
Chapter 12 – Electrical Properties
• Typically materials fall into three categories
– Conductors – metals are good conductors ( ~ 107 (-m)-1)
– Insulators – poor conductors ( ~ 10-10 – 10-20 (-m)-1)
– Semiconductors – in the middle ( ~ 10-6 – 104 (-m)-1)
• Electronic/ionic conduction
– Electric current results from the motion of electrically charged
particles due to forces acting on them from an externally applied
electric field
– Positive charges – accelerated in field direction, negatively
charges – accelerated in opposite direction
– In most solids a current arises from the flow of electrons
(electronic conduction)
– In ionic solids – a net motion of ions is possible that can produce
a current (ionic conduction)
Chapter 12 – Electrical Properties
• Band structures in solids
– You are used to thinking of electron energy states as being very
well defined (molecular orbital theory)
– For solids containing larger numbers of atoms this becomes
blurred
This is what happens when 12
atoms approach one another
(note r is the x-axis)
Electron energies start to split
(this is due to interactions
between atoms)
This is only relevant when the
atoms come close together (i.e.
bonded)
CONDUCTION & ELECTRON TRANSPORT
• Metals:
-- Thermal energy puts
many electrons into
a higher energy state.
• Energy States:
-- the cases below
for metals show
that nearby
energy states
are accessible
by thermal
fluctuations.
6
Chapter 12 – Electrical Properties
• Band structures in solids
– Another picture --
Why does this matter?
Whether or not there is an energy
band gap, and if so, how large it
is, determines the electrical
properties of materials
Why?
For N atom solid
s band has N states
p band has 3N states
Can have empty or partially filled
bands
Electrical properties are a
consequence of the band
structure!
Chapter 12 – Electrical Properties
• Band structures in solids
– Four types of band structures are possible at 0 K
Ef – Fermi level: highest filled state at 0 K
The four figures above are the key point of this chapter – we’ll go through them one
at a time!
Nomenclature – valence band (filled states), conduction band (empty band)
Band gap – electrons are not allowed to have energies in this range
Chapter 12 – Electrical Properties
• Band structures in solids
– Band structure below – metal
• Outermost band below the band gap (what is the
band gap?) is only partially filled
– Can see this for metals, particularly metals with
one 1 s electron (e.g. Cu)
– Have N copper atoms, the 4s band can
accommodate 2N 4s electrons
– Based on this should Cu be a good conductor?
Chapter 12 – Electrical Properties
• Band structures in solids
– Band structure below – metal (why do you think that is?)
• Overlap between an empty band and a filled band
(e.g. Mg)
• For Mg the 3s and 3p energy bands overlap
• Why do you think this is a good conductor?
Chapter 12 – Electrical Properties
• Band structures in solids
– Insulators/semiconductors
• Both of these are similar
• Well defined energy difference between the
filled valence band and the empty conduction
band
• Large energy difference (band gap) – the material
is an insulator (Large? > 2.0 eV (3.2x10-19J))
• Small (< 2.0 eV) band gap – semiconductor
ENERGY STATES: INSULATORS AND
SEMICONDUCTORS
• Insulators:
--Higher energy states not
accessible due to gap.
• Semiconductors:
--Higher energy states
separated by a smaller gap.
7
Chapter 12 – Electrical Properties
• Conduction and Band Structure
– Few more critical concepts
• Only electrons with energies greater than the Fermi energy can be
acted on/accelerated in an applied electric field
• These electrons (free electrons) participate in the conduction
process
• Another important quantity – hole – we see what these are later,
and they also participate in the conduction process (they actually
have energies less than Ef, we’ll see why in a minute)
– As we will see the conductive properties of materials (i.e.
whether they are conductors, semiconductors, or insulators)
depend on the number of free electrons and hole charge carriers
Chapter 12 – Electrical Properties
• Conduction and Band Structure
– Metals
• For electrons to become free (mobile) they must be excited into one
of the empty energy states above the Fermi level
• Typically this does not require much energy
– Applied fields can excite large numbers of electrons into excited
states
• This is why metals conduct!
Chapter 12 – Electrical Properties
• Conduction and Band Structure
– Insulators/Semiconductors
• There are no longer empty states adjacent to the valence band that
can be filled
• Must promote electrons across the band gap (Eg)
• Gap is large enough, non electrical processes are needed to excite
the electrons
• As band gap increases, fewer electrons can be excited into the
conduction band (make sense?) – material has lower conductivity!
Whether a material is an insulator or
semiconductor depends on the width
of the band gap
Another point: increasing
temperature usually causes
conductivity to increase (why?)
Chapter 12 – Electrical Properties
• Electron mobility
– Electric field applied  results in force on free electrons which
experience an acceleration in a direction opposite to that of the
field
– Theoretically there is no interaction between free electrons and a
perfect crystal lattice
– In practice this is not true – one observes that the current reaches
a constant value (immediately) after it is applied
– “Frictional” forces – free electrons scattered by imperfections,
defects, impurities, etc.
• Causes a loss in kinetic energy and change in direction
METALS: RESISTIVITY VS T, IMPURITIES
• Imperfections increase resistivity
--grain boundaries
--dislocations
--impurity atoms
--vacancies
These act to scatter
electrons so that they
take a less direct path.
• Resistivity
increases with:
--temperature
--wt% impurity
--%CW (cold work,
See section on Strain
hardening, Ch. 7)
Adapted from Fig. 18.8, Callister 6e. (Fig. 18.8 adapted from
J.O. Linde, Ann. Physik 5, p. 219 (1932); and C.A. Wert and
R.M. Thomson, Physics of Solids, 2nd ed., McGraw-Hill Book
Company, New York, 1970.)
r  r thermal
 rimpurities
 r def
8
EX: ESTIMATING CONDUCTIVITY
• Question:
--Estimate the electrical conductivity of a Cu-Ni alloy
that has a yield strength of 125MPa.
Adapted from Fig.
7.14(b), Callister 6e.
r  30x10
8
Ohm  m
Adapted from Fig.
18.9, Callister 6e.
1
   3.3x10 6 (Ohm  m) 1
r
9
Chapter 12 – Electrical Properties
• Electron mobility
– The scattering phenomenon is manifested as a resistance to the
passage of an electric current
– Several parameters are used to describe this including the drift
velocity and mobility
– Drift velocity represents the average electron velocity in the
direction of the force imposed by the applied field
 d  e E
e – mobility, E – Electric field
e [=] m2/V-s
• The conductivity of most materials can be expressed as
  n e e
n - # of free e-’s per unit volume
Chapter 12 – Electrical Properties
• Read 12.8, 12.9!
• Semiconductivity
– While not as high as the conductivities of metals, semiconductors
have unique electrical properties
– Why is this? Their electrical properties are extremely sensitive to
the presence of minute concentrations of impurities
– Intrinsic semiconductors – the electrical behavior is based on
the electronic structure inherent in the pure material
– Extrinsic semiconductors – the electrical behavior is dictated
by impurity atoms
Chapter 12 – Electrical Properties
• Intrinsic semiconduction
– Band gap structure shown below
• Two elemental semiconductors are Silicon and Germanium (band
gap energies of 1.1 and 0.7 eV respectively)
– There are many compounds that exhibit semiconducting
properties (GaAs, InSb, CdS, ZnTe)
Chapter 12 – Electrical Properties
• Intrinsic semiconduction
– Hole – for every electron excited into the conduction band there is
left behind a missing electron in one of the covalent bonds, or in
the band scheme, a vacant electron state in the valence band
– Electrons and hole move in opposite directions in the applied field
Chapter 12 – Electrical Properties
• Intrinsic semiconduction
– Two types of charge carrier – the expression for electrical
conduction needs to account for this
  n e e  p e  h
  ni e e  h 
Include term for holes – note n = p = ni
ni is the intrinsic carrier concentration
Chapter 12 – Electrical Properties
• Extrinsic semiconduction
– Here the key is the ability to control very precisely the impurity
content (e.g. 1 atom in 1012!)
– Virtually all commercial semiconductors are extrinsic
– Two types: n-Type and p-Type
• n-Type extrinsic semiconduction
– Incorporate impurity atom with more valence electrons than the
matrix atoms (P into Si)
– The extra non-bonding electron can be readily removed from the
impurity atom (interaction w/P ~ 0.01 eV)
Chapter 12 – Electrical Properties
• n-Type extrinsic semiconduction
– From a band gap view
– This extra electron (donor impurity) is located within the band gap
just below the conduction band (see below)
– Since the impurity atom donates an electron to the conduction
band this type of impurity is referred to as a donor
– Note that here no hole is created within the valence band (why?)
At RT sufficient thermal energy to
excite large numbers of electrons
from donor states
Number of electrons in the
conduction band far exceeds the
number of holes in the valence band
n-type extrinsic semiconductor
Chapter 12 – Electrical Properties
• n-Type extrinsic semiconduction
– Few more points
• Since the number of electrons in the conduction band far exceed
the number of holes in the valence band
  n e e
– The electrons are called the majority carriers, the holes are the
minor charge carriers
– The Fermi level is shift upward in the band gap, closer to the
donor states (exact position depends on T and concentration
(sections 12.12, 12.13))
PURE SEMICONDUCTORS:
CONDUCTIVITY VS T
• Data for Pure Silicon:
-- increases with T
--opposite to metals
undoped  e
Egap / kT
electrons
can cross
gap at
higher T
Adapted from Fig. 19.15, Callister 5e. (Fig. 19.15
adapted from G.L. Pearson and J. Bardeen, Phys.
Rev. 75, p. 865, 1949.)
material
Si
Ge
GaP
CdS
band gap (eV)
1.11
0.67
2.25
2.40
Selected values from
Table 18.2, Callister 6e.
10
CONDUCTION IN TERMS OF
ELECTRON AND HOLE MIGRATION
• Concept of electrons and holes:
• Electrical Conductivity given by:
# holes/m3
  ne  e  p e  h
# electrons/m 3
Adapted from Fig. 18.10,
Callister 6e.
hole mobility
electron mobility
11
INTRINSIC VS EXTRINSIC CONDUCTION
• Intrinsic:
# electrons = # holes (n = p)
--case for pure Si
• Extrinsic:
--n ≠ p
--occurs when impurities are added with a different
# valence electrons than the host (e.g., Si atoms)
• N-type Extrinsic: (n >> p)
• P-type Extrinsic: (p >> n)
Phosphorus atom
Boron atom
hole
4+ 4+ 4+ 4+
  n e e
4+ 5+ 4+ 4+
4+ 4+ 4+ 4+
no applied
electric field
conduction
electron
valence
electron
Si atom
4+ 4+ 4+ 4+
4+ 3+ 4+ 4+
  p e h
4+ 4+ 4+ 4+
no applied
electric field
12
Chapter 12 – Electrical Properties
• p-Type extrinsic semiconduction
– Now the impurity is a trivalent atom (boron or gallium are the
typical culprits)
– Now one of the covalent bonds is deficient one electron
• Hole weakly bond to the atom
– Hole can migrate by the transfer of an electron from an adjacent
bond
– More pictures …
Chapter 12 – Electrical Properties
• p-Type extrinsic semiconduction
– From a band gap picture
– Each impurity atom introduces an energy level within the band
gap, above yet close to the top of the valence band (often
referred to as the impurity electron state)
– Hole subsequently created in the valence band – however only
one carrier is produced; a hole in the valence band
– No free electrons are created
Chapter 12 – Electrical Properties
• p-Type extrinsic semiconduction
– This type of impurity is called an acceptor as it accepts an
electron from the valence band and generates a hole
– Energy level within the band gap is called an acceptor state
– Holes are present in much higher concentrations than free
electrons (p >> n)
– Material is referred to as p-type because positively charged
particles (holes) are primarily responsible for electrical
conduction
– Holes – majority carriers, electrons – minority carriers
  p e h
Chapter 12 – Electrical Properties
• p-Type extrinsic semiconduction
• Fermi level is positioned within the band gap and near the acceptor
level
• Both n- and p- type extrinsic semiconductors are produced from
materials initially of extremely high purity (~ 10-7 at%)
• Key – very high degree of control over the addition of impurity atoms
(doping)
Chapter 12 – Electrical Properties
• Temperature dependence of Carrier Concentration
– Intrinsic semiconductors
• Concentration goes up as temperature goes up –
why is that?
– Extrinsic semiconductors
• Things are more complicated here!
• Plot below: Si doped w/1021 m-3 P atoms
• 3 regions
– Lowest T – freeze out region
» Charged carriers are “frozen” to dopant
atoms
– Intermediate region (Extrinsic)
» n-type: concentration of carriers is constant
» Explain why!
– High temperature (intrinsic)
» Explain this to me!
Chapter 12 – Electrical Properties
• Factors that affect carrier mobility
– Conductivity of a material is dependent not only on the electron and/or
hole concentration, but also their mobility
– Dopant content (extrinsic semiconductors)
• At low dopant contents (~ 1021 m-3),
mobilities are at their maximum
• Higher contents, mobility decreases
• Note e > h
• Carrier mobility
• Temperature effects
– Mobility generally goes down with temperature (thermal
scattering)
– Mobility goes down with dopant concentration
Chapter 12 – Electrical Properties
• Example 12.1
• For intrinsic gallium arsenide (GaAs), the room-temperature
electrical conductivity is 10-6 (-m)-1; the electron and hole mobilities
are 0.85 and 0.04 m2/V-s. What is ni?
  ni e h  e 
need ni
ni 

e  h   e 
10 6   m 
ni 
1.6 10 19 C 0.89m 2 / V  s
1

ni  7.0 1012 m 3

Chapter 12 – Electrical Properties
• Example 12.2
• What is the conductivity of pure (intrinsic) silicon at 150 C
How are going to solve this? What do you need?
  ni e h  e 
How do you get these quantities?
Get ni from carrier concentration vs.
T (Fig 12.15)
ni  4 1019 m 3
Now what ?
 e 0.06m 2 / V  s
 h  0.022m 2 / V  s
  4 1019 m 3 1.6 10 19 C 0.082m 2 / V  s 
  0.52  m 1
DOPED SEMICON: CONDUCTIVITY VS T
• Data for Doped Silicon:
-- increases doping
--reason: imperfection sites
lower the activation energy to
produce mobile electrons.
• Comparison: intrinsic vs
extrinsic conduction...
--extrinsic doping level:
1021/m3 of a n-type donor
impurity (such as P).
--for T < 100K: "freeze-out"
thermal energy insufficient to
excite electrons.
--for 150K < T < 450K: "extrinsic"
--for T >> 450K: "intrinsic"
Adapted from Fig.
18.16, Callister 6e.
(Fig. 18.16 from S.M.
Sze, Semiconductor
Devices, Physics, and
Technology, Bell
Adapted from Fig. 19.15, Callister 5e. (Fig. 19.15
adapted from G.L. Pearson and J. Bardeen, Phys.
Rev. 75, p. 865, 1949.)
Telephone
Laboratories, Inc.,
1985.)
13
Chapter 12 – Electrical Properties
• Hall Effect
– How do you determine the majority charge carrier type, concentration,
and mobility?
– Can’t get this from conductivity measurements!
– Perform Hall effect experiment (see below)
• Apply electrical field to sample (left) so
that electrons/hole move along x
• Apply magnetic field (Bz) along z
• This magnetic field induces a voltage
perpendicular both to the magnetic
field and the current along x
• The magnetic field results in a
force on the holes/electrons such
that they are deflected along y
• Gives rise to the Hall voltage (VH)
Chapter 12 – Electrical Properties
• The magnetic field results in a force on the holes/electrons such that
they are deflected along y
•
Gives rise to the Hall voltage (VH)
RH I x Bz
VH 
d
• RH is the Hall coefficient, which is constant for a
given material
• For metals, conduction is by electrons so
1
RH 
ne
e 

ne

and
e  RH 
Determining the majority carrier, mobility for
semiconductors is more complicated
Chapter 12 – Electrical Properties
• Semiconductor devices
– OK, time for some engineering!
– Point: electrical properties of semiconductors allow them to be used to
perform electronic functions – diodes, transistors
– Advantages: small size, low power consumption, no warmup time
– In short, these are the workhorse of the semiconductor industry and why
your phone is so small!
Chapter 12 – Electrical Properties
• p-n Rectifying Junction
– Rectifier/diode – permits current to flow in one direction only. A rectifier
can transform alternating current to direct current
– Construct p-n rectifying junction from a single piece of semiconductor
doped such that one side is n-type and the other is p-type
• Why can’t you join pieces of n- and p- type materials?
No voltage
At the junction electrons and holes recombine
The p-n rectifying junction
• The p-n junction possesses some interesting properties
which have useful applications in modern electronics.
• P-doped semiconductor is relatively conductive. The same
is true of N-doped semiconductor, but the junction
between them is a nonconductor.
• This nonconducting layer, called the depletion zone,
occurs because the electrical charge carriers in doped ntype and p-type silicon (electrons and holes, respectively)
attract and eliminate each other in a process called
recombination.
• By manipulating this nonconductive layer, p-n junctions
are commonly used as diodes: electrical switches that
allow a flow of electricity in one direction but not in the
other (opposite) direction.
• This property is explained in terms of the forward-bias
and reverse-bias effects, where the term bias refers to an
application of electric voltage to the p-n junction.
P-n junction: forward bias
With this set-up, the ‘holes' in the P-type region and the electrons in the N-type
region are pushed towards the junction. This reduces the width of the depletion zo
The positive charge applied to the P-type block repels the holes, while the
negative charge applied to the N-type block repels the electrons. As electrons and
holes are pushed towards the junction, the distance between them decreases.
This lowers the barrier in potential. With increasing bias voltage, eventually the
nonconducting depletion zone becomes so thin that the charge carriers can
tunnel across the barrier, and the electrical resistance falls to a low value.
The electrons which pass the junction barrier enter the P-type region and a curren
flows.
Chapter 12 – Electrical Properties
• p-n Rectifying Junction
– Thus for a forward bias large numbers of charge carriers move across
the semiconductor to the junction
• Reverse bias – now switch potential; holes and electrons move
away from the junction.
Current-Voltage behavior in junctions
At high reverse bias
voltages (~ 100’s V),
large numbers of
charge carriers are
generated. Gives
rise to an abrupt
increase
in current known as
breakdown
Forward bias – appreciable current, low resistivity
Reverse bias – highly insulative (low current, high
resistance)
Chapter 12 – Electrical Properties
• p-n Rectifying Junction
– Great!? What does this have to do with electronics
– By switching the bias you control current flow through the junction
– Why? Current in the reverse bias mode IR is very small compared to
that in forward bias mode IF
IR << IF; this is called rectification
P-N RECTIFYING JUNCTION
• Allows flow of electrons in one direction only (e.g., useful
to convert alternating current to direct current.
• Processing: diffuse P into one side of a B-doped crystal.
• Results:
--No applied potential:
no net current flow.
--Forward bias: carrier
flow through p-type and
n-type regions; depletion zone
is reduced; current flows.
--Reverse bias: carrier
flow away from p-n junction;
carrier conc. greatly reduced
at junction; little current flow.
14
Chapter 12 – Electrical Properties
• Transistors
– Perform two primary functions
• Amplify electrical signals
• Serve as switching devices for processing/storing information
– Talk about two major types here
• Junction (bimodal) transistor
• Metal oxide semiconductor field-effect transistor (MOSFET)
Chapter 12 – Electrical Properties
• Transistors
– Junction transistors
• Basic idea: two p-n junctions arranged back to back (either n-p-n or
p-n-p) – talk about p-n-p here
• Place thin n-type base region between the two p-type regions; one
is called the emitter and the other is called the collector
• Note biasing of the circuitry
• Transistors
– Junction transistors – how they work
• Given forward bias, large numbers of holes enter the base region. While
some recombine with electrons, if the material is properly designed,
most are swept through the base without recombining and into junction
two
• Since there is a reverse bias on the output side (into the collector), holes
are effectively driven away from junction 2
• Small increase in input voltage within emitter-base circuit leads to large
increase in current across junction 2 (collector current), leads to large
increase in voltage across load resistor
Chapter 12 – Electrical Properties
• Transistors
– Junction transistors – how they work
• Aside: can also make n-p-n transistors: main difference – electrons,
not holes, are injected across the base and into the collector
• Metal oxide semiconductor field effect transistor
(MOSFET)
– Two small islands of a p-type semiconductor within a substrate
of n-type silicon. Islands joined by a narrow p-type channel
– Have metal connects to islands; form an insulating layer on the
surface by oxidizing silicon
• Key point: conductivity of the channel is varied by the
presence of an electrical field on the gate
• (MOSFET)
• Physics: conductivity of the channel is varied by the
presence of an electrical field on the gate
– Impose positive field on gate – drive charge carriers (holes) out
of the channel, reducing conductivity
– Small alteration of field at the gate produces a relatively large
variation in current between the source and drain
– Key difference w/junction transistor – gate current is exceedingly
small as compared to the junction transistor
– Majority carrier dominates MOSFET behavior, minority carriers
play a role with junction transistors
Manipulate
V at gate
to vary
current betwee
source and
drain
Chapter 12 – Electrical Properties
• Semiconductors in computers
– Transistors amplify electrical signals
– They can also be used as switching devices
• Used for arithmetic, logic and storing functions
– Numbers in computers are represented in binary code
(0 or 1)
– Transistors can operate as a “two state” switch
• On or off (conducting/non-conducting)
– Please read about microelectronic circuitry (p 507)
Chapter 12 – Electrical Properties
• Electrical
conduction in
ionic
ceramics &
polymers
– Short story –
most are not
good
conductors
(i.e. they are
insulators)
– High T –
conductivity
does go up
Read 12.16, 12.17
Chapter 12 – Electrical Properties
• Dielectric behavior
– A dielectric material is one that is electrically insulating
(nonmetallic) and exhibits or can be made to exhibit an electric
dipole structure
• Huh? It can separate positively and negatively charged entities on
a molecular/atomic scale
Remember this from physics?
• These are used as capacitors
Chapter 12 – Electrical Properties
• Dielectric behavior
– Apply a voltage across a capacitor – one plate is negatively
charged, the other is positively charged. The capacitance
relates to the amount of charge stored on either plate
C
Q
, C[]C / V or Farad F
V
– If I have a parallel plate capacitor with vacuum between the
plates the capacitance can be calculated as
C  o
A
, A plate area, l distance between plates
l
 o  Permittivi ty of vacuum (8.85 10 12 F / m)
Chapter 12 – Electrical Properties
• Dielectric behavior
– Now, put a dielectric material between the plates
A
C 
l
–  is permittivity of the material (greater than o). The relative
permittivity (dielectric constant) is given by

r 
– Note this quantity is always greater than one, and is the key  o
property for a capacitor
Chapter 12 – Electrical Properties
• Field vectors and polarization
– Way to describe the phenomena of capacitance
– For every electric dipole there is a separation of charge – the
electric dipole moment (p) associated with each dipole is
p  qd
– The dipole moment is actually a vector; in the presence of an
electric field a force is exerted on the dipole to orient it with the
applied field; this is called polarization
– For a dielectric material in a capacitor the surface charge density
is given as
D  E
– This is also sometimes called the dielectric displacement
Chapter 12 – Electrical Properties
• Field vectors and polarization
– Can explain increase in capacitance using a model of
polarization within a dielectric material: consider the
figures below
In the case above (vacuum)
the charge is on the plates
In the case above the entire solid (dielectric)
becomes polarized. Net accumulation of
charge in the dielectric near the plate
surface. No net charge in the middle of the
material, but the charge accumulation at the
edges is facilitated by polarization
Chapter 12 – Electrical Properties
• Field vectors and polarization
– Due to polarization of the dielectric there is
accumulation of negative charge (-Q’) near the
surface of the positively charged plate
– The induced charge from the dielectric can be thought
of as nullifying some of the charge that originally
existed on the plate when in vacuum
– In the presence of the dielectric the surface charge
density is now given by
E
D  oE  P
P   o  r  1E
May be thought of as a
polarization E field with the
dielectric that results from
alignment of the dipoles
Chapter 12 – Electrical Properties
• Types of polarization
– Three sources of polarization: electronic, ionic,
orientation
– Electronic: can be induced in all atoms. Due to
displacement of the center of the electron cloud from
the nucleus by the electric field
– Ionic: Found in ionic materials. Electric fields
displaces cations and anions in opposite directions
– Orientation: Only found in substances with a
permanent dipole moment
• Dipoles align with the field
• Frequency dependence of the dielectric constant
– This matters because in many cases the current is alternating, or
the applied voltage changes direction with time
– As voltage “switches” the dipoles attempt to reorient with the field
– This reorientation takes some finite amount of time – the
relaxation frequency is the reciprocal of the minimum
reorientation time
What happens if the
frequency of the applied
electric field exceeds the
relaxation frequency of
the dielectric material?
• Frequency dependence of the dielectric constant
– What happens if the frequency of the applied electric field
exceeds the relaxation frequency of the dielectric material?
• The dipoles cannot keep shifting their orientation – that dipole will
not contribute to the dielectric constant
• See abrupt
changes in r as
different
mechanisms are
“turned off”
• Absorption of
energy by a
dielectric material
subjected to an
alternating field is
called the
“dielectric loss”. A
low loss is desired
– why?
Chapter 12 – Electrical Properties
• Dielectric strength
– What can happen to a material if you put a large voltage/electric
field on it?
– Can turn it into a conductor!
– This can lead to material degradation/failure
• Clearly don’t want this to happen!
– The dielectric strength is the electric field needed to induce
breakdown of a material
SUMMARY
• Electrical conductivity and resistivity are:
--material parameters.
--geometry independent.
• Electrical resistance is:
--a geometry and material dependent parameter.
• Conductors, semiconductors, and insulators...
--different in whether there are accessible energy
states for conductance electrons.
• For metals, conductivity is increased by
--reducing deformation
--reducing imperfections
--decreasing temperature.
• For pure semiconductors, conductivity is increased by
--increasing temperature
--doping (e.g., adding B to Si (p-type) or P to Si (n-type).
15
ANNOUNCEMENTS
Reading: Chapter 12
HW 10: Due Monday, April 9th
Problems 12.1; 12.3; 12.6; 12.8; 12.11; 12.16;
12.19; 12.27; 12.28; 12.35; 12.40; 12.43
0